Равнобедренный треугольник и его свойства

Равнобедренный треугольник

и его свойства

Свойство - характеристика, присущая вещам и явлениям, позволяющая отличать их .

..

СВОЙСТВО — СВОЙСТВО, а, ср. Качество, признак, составляющий отличительную особенность кого чего н. … Толковый словарь Ожегова

свойство — свойство особенность, присущая предмету и позволяющая включить его в тот или иной класс предметов. …

Энциклопедический словарь

I. СВОЙСТВО а; ср. кого чего. Существенный признак, качество, отличающее один предмет или одно лицо от другого; отличительная особенность, черта кого, чего либо. … Толковый словарь русского языка Кузнецова

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

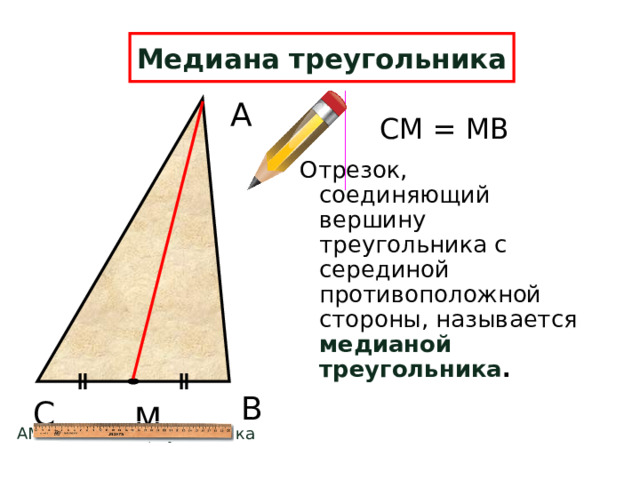
Медиана треугольника

А

СМ = МВ

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника .

В

С

М

АМ – медиана треугольника

Медиана треугольника

Медиана-обезьяна,

У которой зоркий глаз,

Прыгнет точно в

Середину

Стороны против

вершины,

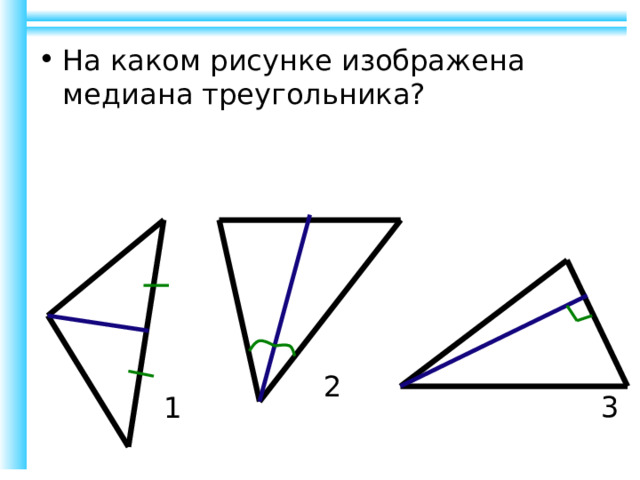
• На каком рисунке изображена медиана треугольника?

2

3

1

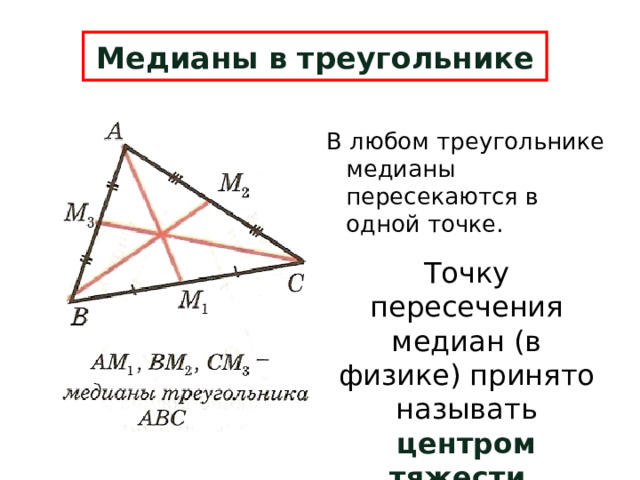
Медианы в треугольнике

В любом треугольнике медианы пересекаются в одной точке.

Точку пересечения медиан (в физике) принято называть центром тяжести .

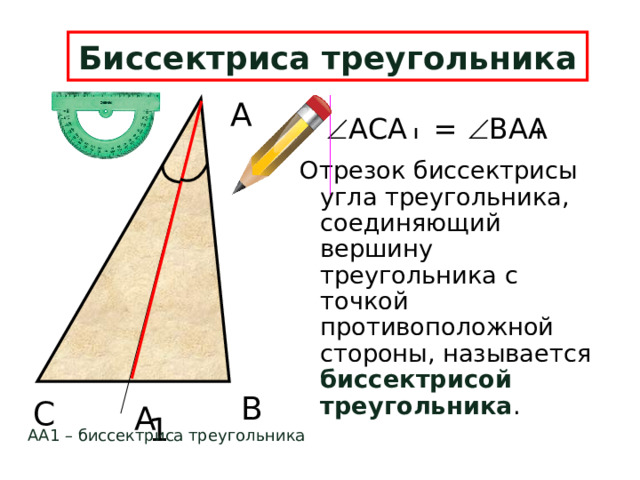
Биссектриса треугольника

А

 АСА =  ВАА

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника .

В

С

А

1

АА1 – биссектриса треугольника

8

Биссектриса треугольника

Биссектриса – это крыса, Которая бегает по углам И делит угол пополам.

8

• На каком рисунке изображена биссектриса?

1

3

2

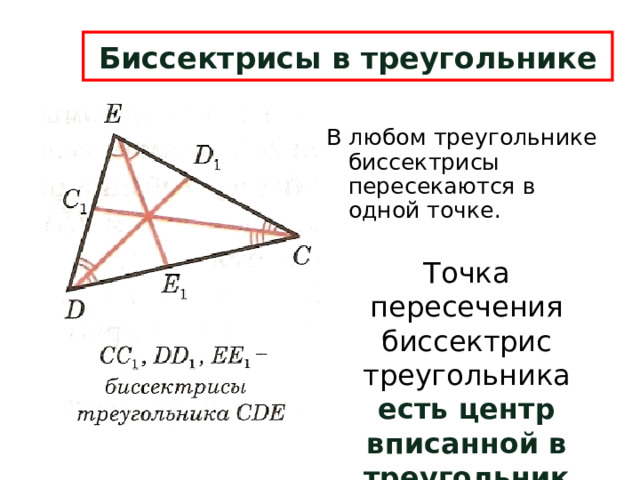
Биссектрисы в треугольнике

В любом треугольнике биссектрисы пересекаются в одной точке.

Точка пересечения биссектрис треугольника есть центр вписанной в треугольник окружности .

8

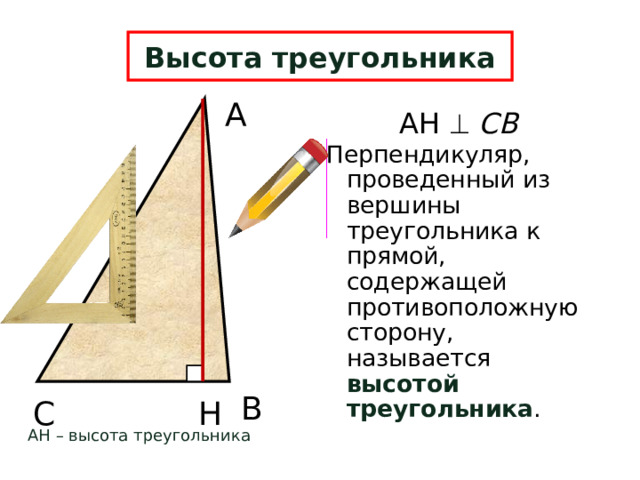
Высота треугольника

А

АН  СВ

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника .

В

Н

С

АН – высота треугольника

8

Высота треугольника

Высота похожа на кота, Который выгнул спину , И под прямым углом Соединяет вершину И сторону хвостом .

8

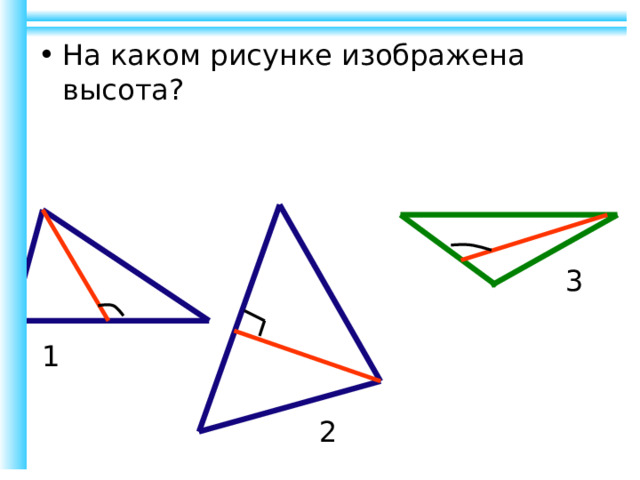
• На каком рисунке изображена высота?

3

1

2

Высоты в треугольнике

8

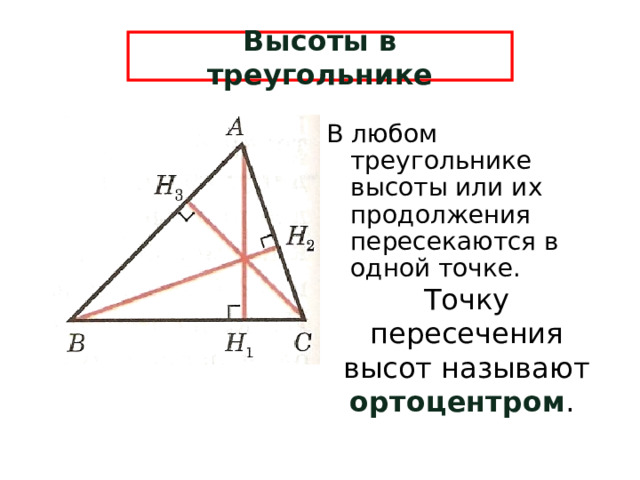
Высоты в треугольнике

В любом треугольнике высоты или их продолжения пересекаются в одной точке.

Точку пересечения высот называют ортоцентром .

8

Повторение основных понятий Тест

1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур .

а ) Отрезок, соединяющий вершину треугольника с серединой

_______________________________________,   называется

  _______________________ треугольника.

противоположной стороны

медианой

б)  Перпендикуляр , проведённый из вершины треугольника к прямой, содержащей противолежащую сторону, называется ______________.

высотой

биссектрисы

в). Отрезок __________________угла треугольника, соединяющий вершину треугольника с точкой противополо-женной стороны, называется _________________________________.

биссектрисой треугольника

2. Верны ли следующие утверждения? а).В любом треугольнике можно провести три медианы .  ____

да

б)  Точка пересечения высот любого треугольника лежит внутри треугольника . _____

в)  Все биссектрисы треугольника пересекаются в одной точке._______

нет

да

Боковая сторона

Боковая сторона

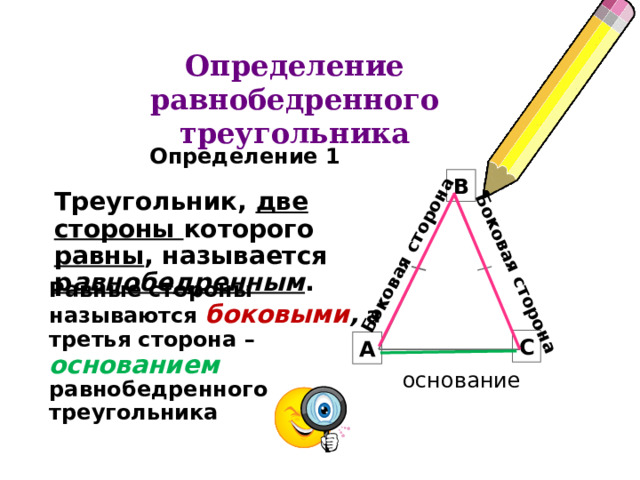
Определение равнобедренного треугольника

Определение 1

B

Треугольник, две стороны которого равны , называется р авнобедренным .

Равные стороны называются боковыми , а третья сторона – основанием равнобедренного треугольника

C

A

основание

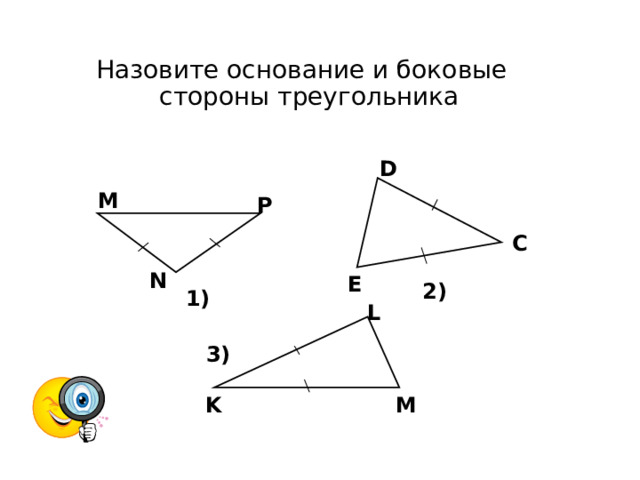
Назовите основание и боковые стороны треугольника

D

М

Р

C

N

E

2)

1)

L

3)

K

M

Практическая работа

• Соединить боковые стороны равнобедренного треугольника, линию сгиба зафиксировать.

• Какие получились треугольники?

Две геометрические фигуры называются равными , если они

совпали при наложении .

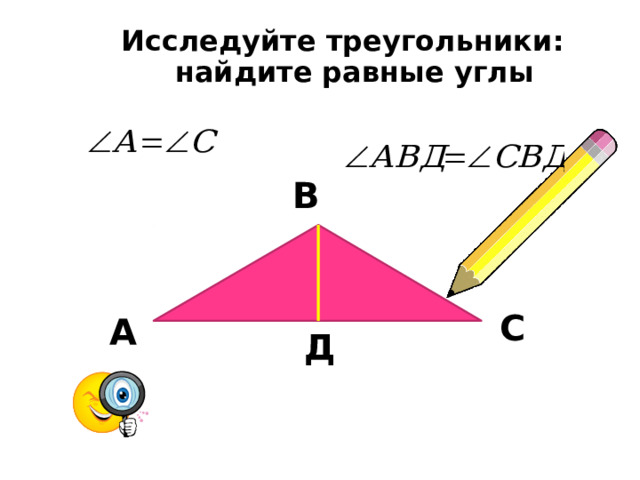
Исследуйте треугольники: найдите равные углы

В

С

А

Д

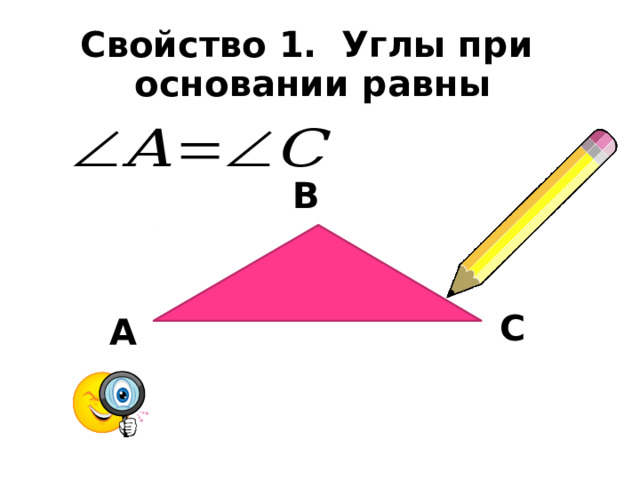
Свойство 1. Углы при основании равны

В

С

А

Практическая работа

• Исследуйте треугольники: найдите равные стороны

• 1 .Может ли линия сгиба являться медианой данного треугольника?
• 2. Может ли линия сгиба являться биссектрисой данного треугольника?
• 3. Может ли линия сгиба являться высотой данного треугольника?

Сделайте выводы.

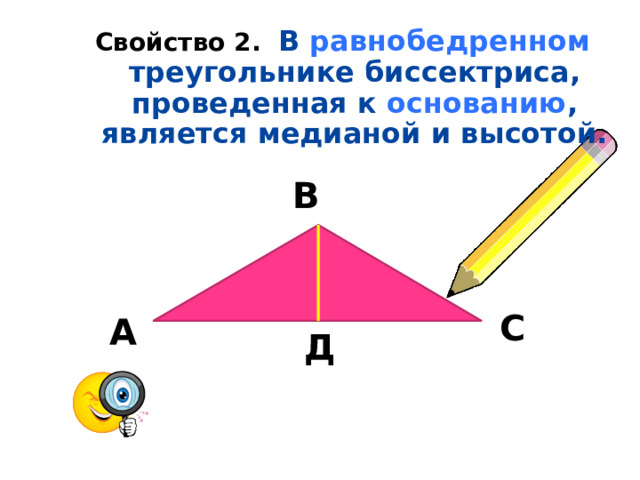
Свойство 2. В равнобедренном треугольнике биссектриса, проведенная к основанию , является медианой и высотой.

В

С

А

Д

:

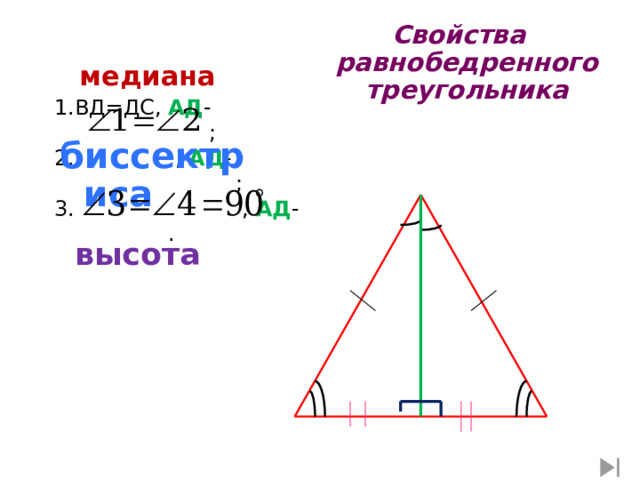
Свойства равнобедренного треугольника

медиана

1.ВД=ДС, АД - ; 2. , АД - ; 3. , АД - .

биссектриса

A

высота

1

2

3

4

B

D

C

21

:

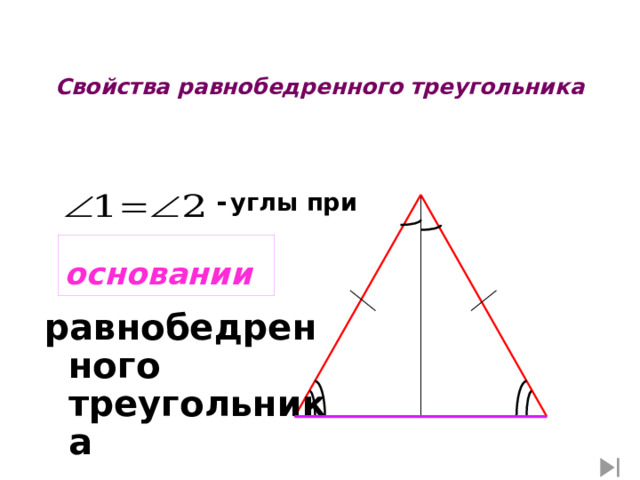
Свойства равнобедренного треугольника

- углы при

A

основании

равнобедренного треугольника

2

1

D

C

B

21

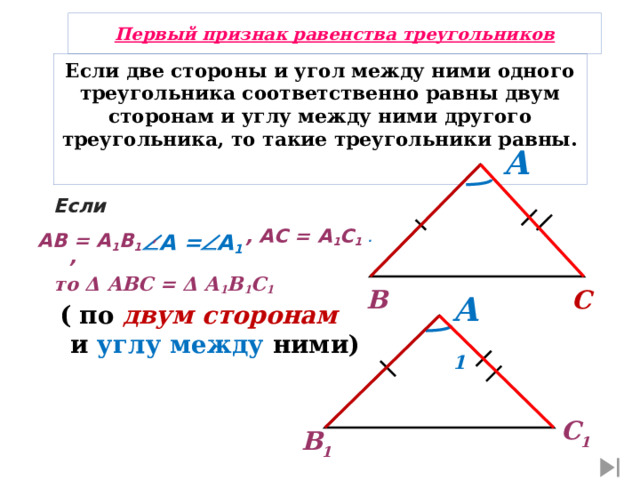
Первый признак равенства треугольников

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

А

Если

, . ,

то Δ АВС = Δ А 1 В 1 С 1

, АС = А 1 С 1

АВ = А 1 В 1

 А =  А 1

В

С

А 1

( по двум сторонам и углу между ними)

С 1

В 1

21

В равнобедренном треугольнике углы при основании равны

Доказательство :

Дано:  АВС – равнобедренный, АС – основание

Доказать:  А =  С

 АВС

1.Проведем биссектрису ВД угла____ .

2.. Рассмотрим  АВD и  СВD:

( С ) а). ВД - сторона;

( У ) б).  АВД= , т.к. ВД- ;

( С) в). АВ= , т.к.  АВС – ;

Значит,  АВD  СВD (по двум сторонам и

)

3. В равных треугольниках против равных сторон лежат

Значит,  А=

Что и требовалось доказать

общая

 СВД

биссектриса

ВС

равнобедренный

B

=

углу между ними

равные углы

 С.

C

A

Д

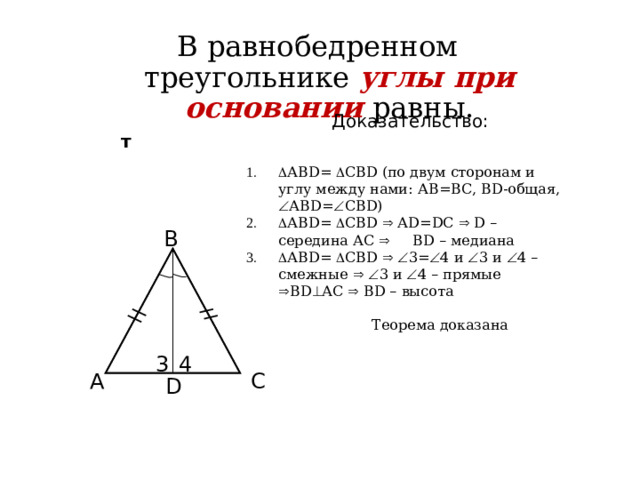
В равнобедренном треугольнике углы при основании равны.

Доказательство:

т

•  АВD=  СВD (по двум сторонам и углу между нами: АВ=ВС, ВD-общая,  АВD=  СВD)
•  АВD=  СВD  АD=DC  D – середина АС  ВD – медиана
•  АВD=  СВD   3=  4 и  3 и  4 – смежные   3 и  4 – прямые  ВD  АС  ВD – высота

Теорема доказана

B

3

4

C

A

D

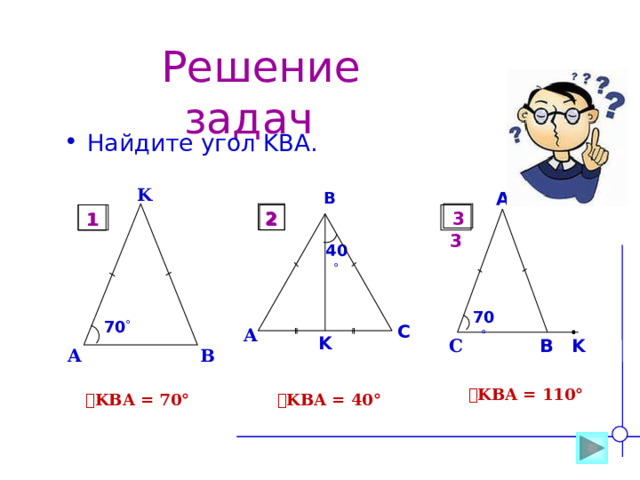
Решение задач

• Найдите угол KBA.

K

A

B

2

3

3

2

1

1

40 

70 

70 

C

A

K

C

K

B

A

B

ے KBA = 110°

ے KBA = 70°

ے KBA = 40°

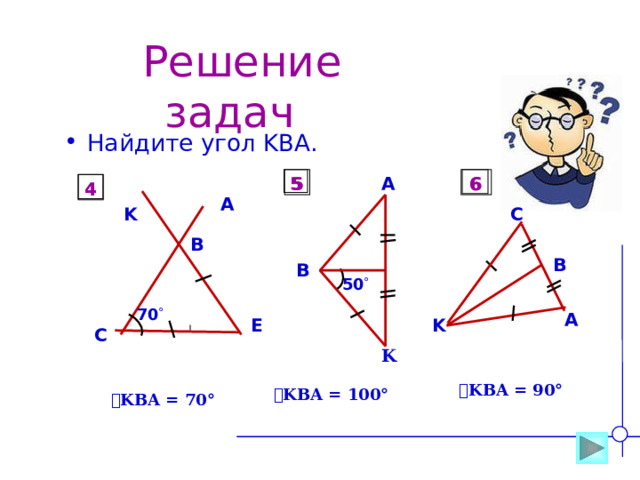
Решение задач

• Найдите угол KBA.

5

6

5

6

A

4

4

A

C

K

B

B

B

50 

70 

A

E

K

C

K

ے KBA = 90°

ے KBA = 100°

ے KBA = 70°

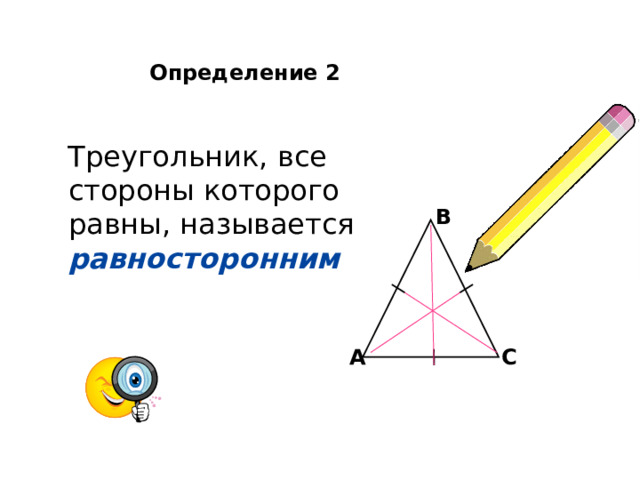
Определение 2

Треугольник, все стороны которого равны, называется равносторонним

B

A

C

Выводы:

• У равнобедренного треугольника углы при основании равны.
• Не всякая биссектриса равнобедренного треугольника является медианой и высотой, а только та, которая проведена из вершины к основанию.

Домашнее задание:

1.доказать свойство 2 равнобедренного треугольника;

2. Выполнить тест;

3. Решить 6 задач с пояснением.