Равноускоренное прямолинейное движение. Графики зависимости кинематических величин от времени при равноускоренном прямолинейном движении.

Тема: Равноускоренное прямолинейное движение. Графики зависимости кинематических величин от времени при равноускоренном прямолинейном движении.

Цель: на наглядном примере изучить равномерное прямолинейное движение с помощью графиков зависимости.

Самое простое из всех неравномерных движений — это прямолинейное движение с постоянным ускорением.

При движении с постоянным ускорением (a→=const−→−−) скорость тела линейно зависит от времени:

v→=v→o+a→t.

В проекциях на ось Ox данные равенства имеют вид:

ax=const;

vx=vox+axt.

Построим графики зависимостей ax(t) и vx(t) для случаев ax0 и ax.

Примем vox0.

Поскольку в обоих случаях ax=const, то графиком зависимости ax(t) ускорения от времени в обоих случаях будет прямая, параллельная оси времени.

Только при ax0 данная прямая будет лежать в верхней полуплоскости (рис. 1), а при ax — в нижней (рис. 2).

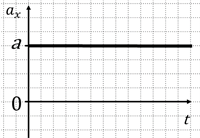
Рис. 1

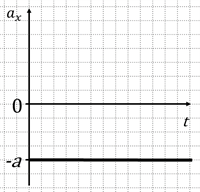
Рис. 2

Графиком зависимости скорости движения тела от времени vx(t) является прямая, пересекающая ось скорости в точке v0 и образующая с положительным направлением оси времени острый угол при ax0 (рис. 3) и тупой угол при ax (рис. 4).

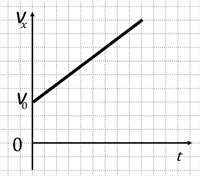
Рис. 3

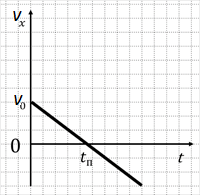
Рис. 4

График на рисунке 3 описывает возрастание проекции скорости vx. При этом модуль скорости тела также растёт. Данный график соответствует равноускоренному движению тела.

График на рисунке 4 показывает, что проекция vx скорости тела вначале положительна.

Она уменьшается и в момент времени t=tп становится равной нулю.

В этот момент тело достигает точки поворота, в которой направление скорости тела меняется на противоположное, и при ttп проекция скорости становится отрицательной.

Из последнего графика также видно, что до момента поворота модуль скорости уменьшался — тело двигалось равнозамедленно.

При ttп модуль скорости растёт — тело движется равноускоренно.

Для любого равнопеременного прямолинейного движения площадь фигуры между графиком vx и осью времени t численно равна проекции перемещения Δrx.

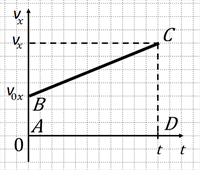
Рис. 5

Согласно данному правилу, проекция перемещения Δrx при равнопеременном движении определяется площадью трапеции ABCD (рис. 5). Эта площадь равна полусумме оснований трапеции, умноженной на её высоту:

S=AB+DC2⋅AD.

В результате:

Δrx=vox+vx2⋅Δt.

Из данной формулы получим формулу для среднего значения проекции скорости:

vxср=ΔrxΔt=vox+vx2.

При движении с постоянным ускорением данное отношение выполняется не только для проекций, но и для векторов скорости:

vcp−→=vo→+v→2.

Средняя скорость движения с постоянным ускорением равна полусумме начальной и конечной скоростей.

Зависимость проекции перемещения от времени при равноускоренном движении имеет вид:

Δrx=v0xt+axt22.

Учитывая, что проекция перемещения движущегося тела равна:

Δrx=x−x0 —

зависимость координаты движущегося тела от времени имеет вид:

x=x0+v0xt+axt22.

Последняя формула выражает кинематический закон равнопеременного движения.

Поскольку при равнопеременном движении зависимости перемещения и координаты тела от времени являются квадратичными функциями, то графиками зависимости данных величин от времени являются участки парабол.

На рисунке 1 представлены графики зависимости скорости движения тела при ax=a0 (прямая 1), при ax=a=0 (прямая 2) и при ax=a (прямая 3).

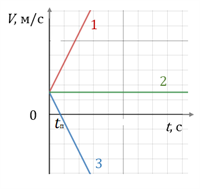
Рис. 1

На рисунке 2 представлены графики зависимости проекции перемещения движущегося тела от времени при ax=a0 (кривая 1), при ax=a=0 (прямая 2) и при ax=a (кривая 3).

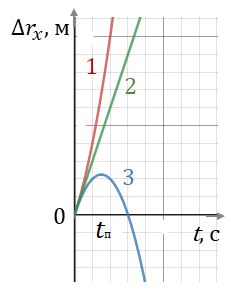
Рис. 2

При ax=a0 проекция перемещения всё время увеличивается (кривая 1).

А при ax=a проекция перемещения увеличивается до момента времени t=tп, а затем уменьшается. Это происходит потому, что в момент времени tn скорость тела становится равной нулю, а направление его движения меняется на противоположное, то есть происходит поворот.

Моменту времени tn на кривой 3 рисунка 2 соответствует вершина параболы.

График зависимости пути s от времени при движении, направление скорости при котором не изменяется, совпадает с графиком зависимости проекции перемещения от времени (рис. 3, кривые 1 (график проекции перемещения) и 2 (график пути)).

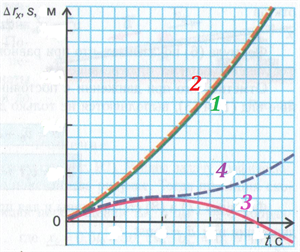
Рис. 3

Если же направление скорости во время движения изменяется, то есть происходит поворот, то эти графики совпадают только при 0ttn (рис. 3, кривые 3 (график проекции перемещения) и 4 (график пути)).

После момента поворота tn проекция перемещения начинает уменьшаться, а путь продолжает увеличиваться. При этом путь увеличивается на столько, на сколько за то же время уменьшается проекция перемещения.

График зависимости координаты от времени (рис. 4, кривые 1 и 3) получается из графика зависимости перемещения от времени (рис. 4, кривая 2) смещением последнего на величину |x0| вверх при x00 (рис. 4, кривая 1) или вниз при x0 (рис. 4, кривая 3), поскольку x=x0+Δrx (рис. 4).

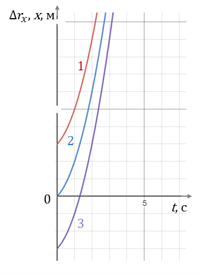
Рис. 4