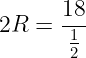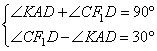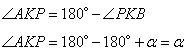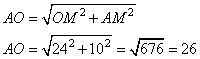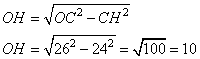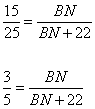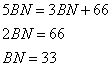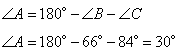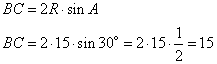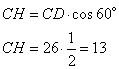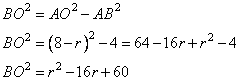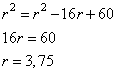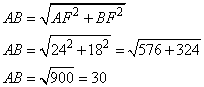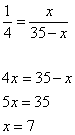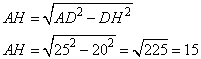Разбор 23 задания ОГЭ

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.

Решение:

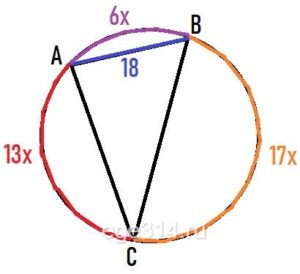
    Длины дуг относятся как 6:13:17. Пусть ‿АВ = 6х, ‿АС = 13х, ‿ВС =17х. Вся окружность равна 360°. Найдём ‿АВ:

‿АВ + ‿АС + ‿ВС = 360º
6х + 13х + 17х = 360
36х = 360
х = 360/36 = 10
‿АВ = 6х = 6·10 = 60º

    Вписанный угол (∠С) всегда в два раза меньше дуги на которую опирается:

∠С = ‿АВ/2 = 60/2 = 30º

    По теореме синусов найдём радиус (R) окружности:

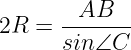
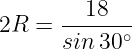
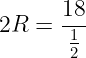
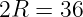
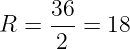
Ответ: 18.

Прямая пересекает стороны АВ и ВС треугольника ABC в точках K и N соответственно. Известно, что АВ = 12, ВС = 15, АС = 24, AK = 7, CN = 11. Найдите длину отрезка KN.

Решение.

В треугольнике KBN: KB = 12-7 = 5, BN = 15-11 = 4. В треугольниках ABC и NBK угол В общий и

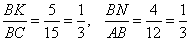
Следовательно, треугольники ABC и NBK подобны. Значит,

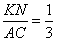
откуда

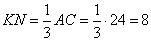
Ответ: 8.

В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К. Известно, что угол AFC равен 150°. Найдите FK, если CF = 12√3.

Решение.

Основания трапеции ABCD параллельны друг другу (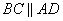 ), следовательно,  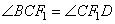 (как накрест лежащие). Также в трапеции  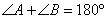, значит,  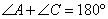. Получаем, что  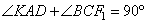. Так как AK и CF1 – биссектрисы, то

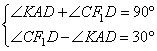
Решаем систему, имеем:

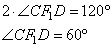
По условию угол AFC=150º, значит, угол CFK=30º, следовательно,

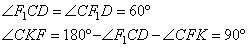
Получаем прямоугольный треугольник CFK с гипотенузой CF. Так как CF=12√3, то

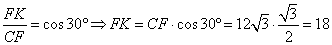
Ответ: 18

Окружность пересекает стороны АВ и АС треугольника ABC в точках K и P соответственно и проходит через вершины В и С. Найдите длину отрезка KP, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ.

Решение.

Пусть сторона BC=x, тогда AB=2x, так как она в 2 раза больше стороны BC по условию задачи. Рассмотрим четырехугольник CPKB, который вписан в окружность. Как известно, у такого четырехугольника сумма противоположных углов равна 180 градусов, то есть 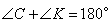  и  . Предположим, что угол 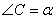 , тогда угол  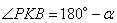, теперь, учитывая, что углы  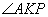 и 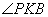  смежные, то угол

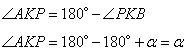
то есть он равен углу 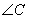 . Аналогично и для угла  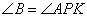. Из равенства этих двух пар углов следует, что треугольники ACB и APK подобны друг другу по двум углам.

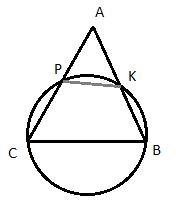
Для подобных треугольников можно записать следующее соотношение:

,

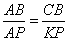откуда

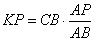
и подставляя числовые значения, имеем:

.

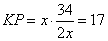Ответ: 17.

Отрезки АВ и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если АВ = 20, CD = 48, а расстояние от центра окружности до хорды АВ равно 24.

Решение.

Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть, 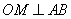 , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=20, то AM=10. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:

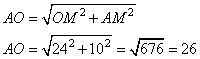
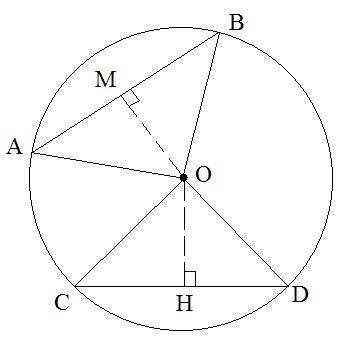
Также это означает, что OC=OD=AO=26. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=24. По теореме Пифагора находим длину OH:

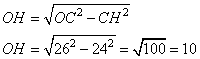
Ответ: 10

 Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=18, а расстояния от центра окружности до хорд AB и CD равны соответственно 40 и 9.

РЕШЕНИЕ:



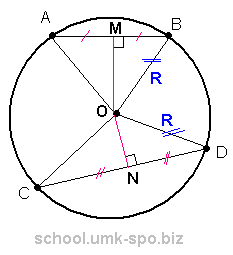
МВ = АВ/2 = 18/2 = 9

∆ВМО = ∆ OND ( OB=OD=R, MB = ON = 9) ⇒ ND = OM = 40

CD = 2 ND = 2 * 40 = 80

Ответ: 80

Прямая, параллельная стороне АС треугольника ABC, пересекает стороны АВ и ВС в точках М и N соответственно. Найдите BN, если MN = 15, АС = 25, NC = 22.

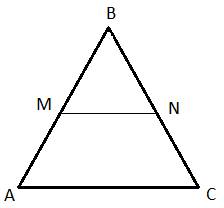
Решение.

По условию задачи в треугольнике ABC прямая 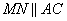 , следовательно, треугольники MBN и ABC подобны по двум углам: угол  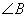 - общий, а углы  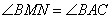 как соответственные при параллельных прямых MN, AC и секущей AB. Из подобия треугольников следует:

.

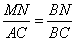Из рисунка видно, что 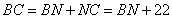 , подставляем числовые значения в отношение, имеем:

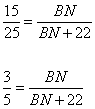
откуда

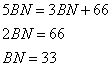
Ответ: 33.

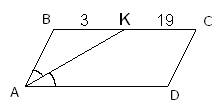
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке K. Найдите периметр параллелограмма, если ВК = 3, CK = 19.

Решение.

Так как ABCD – параллелограмм, то стороны 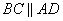 , следовательно, углы  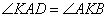 как накрест лежащие при параллельных прямых BC, AD и секущей AK. По условию задачи AK – биссектриса угла A, значит, углы  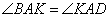 и отсюда получаем, что  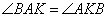. Таким образом, треугольник ABK равнобедренный со сторонами AB=BK=3 и основанием AK. Учитывая, что в параллелограмме противоположные стороны равны, и BC=3+19=22, то периметр равен

.

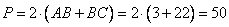Ответ: 50.

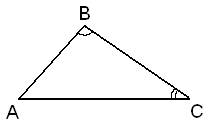
Углы В и С треугольника ABC равны соответственно 66° и 84°. Найдите ВС, если радиус окружности, описанной около треугольника ABC, равен 15.

Решение.

Так как сумма углов в любом треугольнике равна 180 градусов, то угол А равен

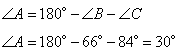
Найдем длину BC из теоремы синусов как

,

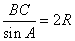где 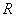  - радиус описанной окружности вокруг треугольника ABC. Отсюда получаем:

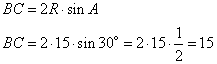
Ответ: 15.

Найдите боковую сторону АВ трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, a CD = 26.

Решение.

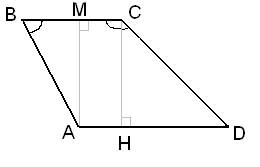
Рассмотрим прямоугольный треугольник CDH, в котором угол 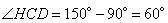 . Так как косинус угла – это отношение прилежащего катета к гипотенузе, то можно записать, что

,

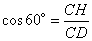откуда

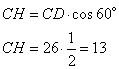
Рассмотрим прямоугольный треугольник ABM, в котором AM=CH. Известно, что синус угла – это отношение противолежащего катета к гипотенузе, то есть, имеем:

,

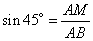откуда

.

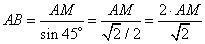Подставляя вместо AM найденное ранее числовое значение, получаем:

.

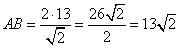Ответ: 13√2.

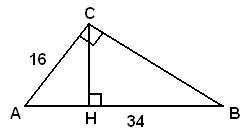
Катет и гипотенуза прямоугольного треугольника равны 16 и 34 соответственно. Найдите высоту, проведённую к гипотенузе.

Решение.

В соответствии со свойством о средних пропорциональных отрезках в прямоугольном треугольнике, катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. То есть в данном случае можно записать:

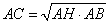
или в виде

,

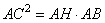откуда

.

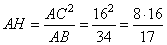Рассмотрим прямоугольный треугольник ACH, в котором известна гипотенуза AC и катет AH, следовательно, высоту CH можно найти по теореме Пифагора:

Ответ:  .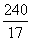

Окружность с центром на стороне АС треугольника ABC проходит через вершину С и касается прямой АВ в точке В. Найдите диаметр окружности, если АВ = 2, АС = 8.

Решение.

Сделаем построение, проведен радиус BO, который будет перпендикулярен стороне AB, так как AB – касательная к окружности по условию задачи (см. рисунок).

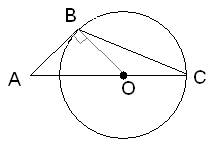
Введем обозначение OB=OC=r – радиусы окружности. Тогда отрезок 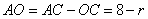 . Выразим квадрат радиуса BO=r  из прямоугольного треугольника ABO по теореме Пифагора, получим следующее выражение:

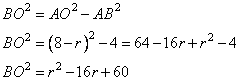
Так как BO=r, получаем уравнение:

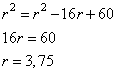
И диаметр окружности равен  .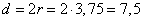

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.

Решение.

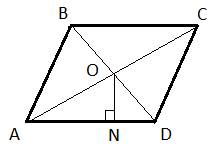
Диагонали ромба являются биссектрисами его соответствующих углов, а точка пересечения O делит диагонали ромба пополам. Отсюда следует, что угол 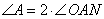 . Рассмотрим прямоугольный треугольник AON (прямоугольный, так как расстояние от точки O до AD – это перпендикуляр, опущенный из точки O). В этом треугольнике известен катет ON=14 и гипотенуза AO=AC:2=56:2=28. Тогда синус угла  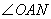 будет равен отношению противолежащего катета ON на гипотенузу AO:

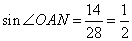
и угол

.

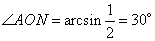Имеем, что угол

.

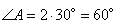Так как противоположные углы в ромбе равны, то 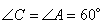 . Сумма односторонних углов в ромбе равна 180 градусов, то есть  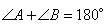 и

,

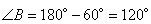соответственно,

.

Ответ: 60, 60, 120, 120.

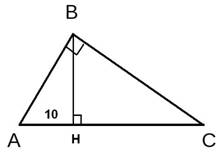
Точка Н является основанием высоты, проведённой из вершины прямого угла В треугольника ABC к гипотенузе АС. Найдите АВ, если АН = 10, АС = 40.

Решение.

В соответствии со свойством о средних пропорциональных отрезках в прямоугольном треугольнике, катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. То есть в данном случае можно записать:

,

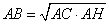и, подставляя числовые значения, имеем:

.

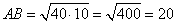Ответ: 20.

Точка Н является основанием высоты ВН, проведённой из вершины прямого угла В прямоугольного треугольника ABC. Окружность с диаметром ВН пересекает стороны АВ и СВ в точках Р и К соответственно. Найдите ВН, если РК = 12.

Решение.

Для решения данной задачи нужно вспомнить, что в любой окружности хорды, проведенные от ее диаметра, всегда пересекаются под углом в 90 градусов. Следовательно, точки P и K находятся на разных концах диаметра окружности, и так как PK=12, то и диаметр окружности равен 12. В задаче сказано, что BH – это диаметр окружности, значит, BH=PK=12.

Ответ: 12.

Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 24, BF = 18.

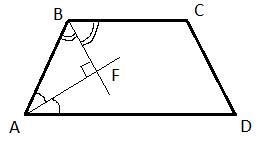
Решение.

У трапеции ABCD основания 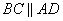 , следовательно, углы  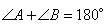 как внутренние односторонние при параллельных прямых. По условию задачи AF и BF – биссектрисы соответствующих углов, тогда сумма углов

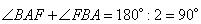
и, следовательно, угол 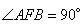  (так как сумма углов в треугольнике ABF равна 180 градусов). Таким образом, имеем прямоугольный треугольник AFB с гипотенузой AB, которую вычислим по теореме Пифагора:

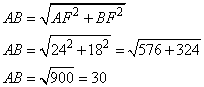
Ответ: 30.

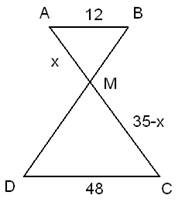
 Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD пересекаются в точке М. Найдите МС, если АВ = 12, DC = 48, АС = 35.

Решение.

Так как 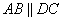 , то углы  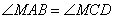 как накрест лежащие углы при параллельных прямых AB, DC и секущей AC. Углы  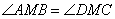 как вертикальные углы. Следовательно, треугольники AMB и CMD подобны по двум углам. Для подобных треугольников можно записать следующее отношение:

.

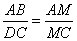Пусть AM=x, тогда MC=AC-AM=35-x, и отношение примет вид:

,

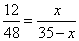откуда

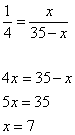
и MC=35-7=28.

Ответ: 28.

Высота АН ромба ABCD делит сторону CD на отрезки DH = 20 и СН = 5. Найдите высоту ромба.

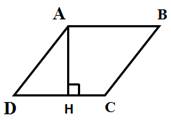
Решение.

Длина стороны DC ромба ABCD, равна

DC=DH+HC=20+5=25.

Так как у ромба все стороны равны, то AD=DC=25. В результате, имеем прямоугольный треугольник, ADH, в котором известна гипотенуза AD и катет DH. Тогда второй катет AH (высота ромба) можно найти по теореме Пифагора:

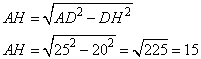
Ответ: 15.