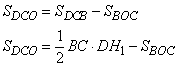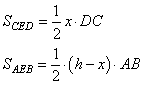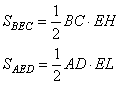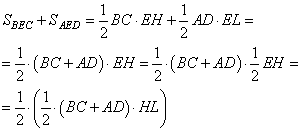Разбор 24 задания ОГЭ

Основания ВС и AD трапеции ABCD равны соответственно 3 и 12, BD = 6. Докажите, что треугольники CBD и BDA подобны.

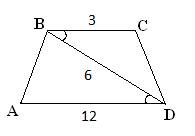
Решение.

Так как ABCD трапеция, то ее основания 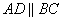 , следовательно, равны и углы  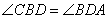 как накрест лежащие при параллельных BC, AD и секущей BD. Рассмотрим треугольники CBD и BDA, у которых имеем следующие пропорци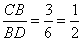и:

 и  .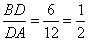

Следовательно, треугольники CBD и BDA подобны друг другу по двум пропорциональным сторонам и равным углам, заключенными между этими сторонами.

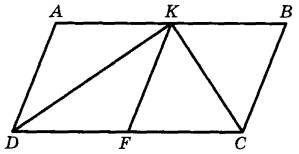
Точка К – середина боковой стороны СD трапеции АВСD. Докажите, что площадь треугольника АВК равна сумме площадей треугольников ВСК и АКD.

Точка K — середина боковой стороны CD трапеции ABCD. Докажите, что площадь треугольника KAB равна половине площади трапеции.

Решение.

Продолжим BK до пересечения с прямой AD в точке F. Заметим, что в треугольниках FDK и BCK стороны CK и DK равны по условию, углы при вершине K равны как вертикальные, а углы KDF и KCB равны как накрест лежащие. Значит, треугольники FDK и BCK равны.

Следовательно, их площади равны, то есть площадь трапеции равна площади треугольника ABF. Но из равенства треугольников также вытекает, что FK = BK, то есть AK — медиана в треугольнике ABF. Тогда треугольник KAB по площади составит половину треугольника FAB, а значит, и данной трапеции.

В треугольнике ABC с тупым углом ACB проведены высоты AA₁ и BB₁. Докажите, что треугольники A₁CB₁ и ACB подобны.

Решение.

Поскольку угол ACB тупой, основания высот A₁ и B₁ будут лежать на продолжениях сторон BC и AC соответственно. Диагонали четырёхугольника AA₁B₁B пересекаются, поэтому он выпуклый. Поскольку ∠AA₁B = ∠AB₁B = 90°, каждый из прямоугольных треугольников AA₁B и AB₁B вписан в окружность с диаметром AB. Это означает, что все вершины четырёхугольника AA₁B₁B лежат на одной окружности. Тогда углы ∠AB₁A₁ и ∠ABA₁ равны как вписанные углы, опирающиеся на дугу A₁A. Аналогично, ∠BA₁B₁ = ∠BAB₁. Значит, указанные треугольники подобны по двум углам.

Укажем общую теорему.

Основания двух высот треугольника (остроугольного или тупоугольного) и одна из его вершин образуют треугольник, подобный исходному; коэффициент подобия равен модулю косинуса их общего угла.

 В треугольнике ABC с тупым углом АСВ проведены высоты АА1 и ВВ1. Докажите, что треугольники A1CB1 и АСВ подобны.

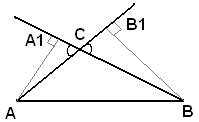
Решение.

Рассмотрим сначала два прямоугольных треугольника AA1C и BB1C, которые подобны по двум углам (один угол у них прямой, а углы 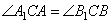  как вертикальные). У подобных треугольников AA1C и BB1C сторона A1C пропорциональна стороне B1C, а сторона AC пропорциональна стороне BC.

Рассмотрим теперь треугольники A1CB1 и ACB, у которых пропорциональны стороны AC, CB и A1C, B1C и равны углы 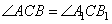 между этими сторонами как вертикальные. По второму признаку подобия два треугольника подобны, если стороны одного треугольника пропорциональны соответствующим сторонам другого треугольника и углы, заключенные между этими сторонами, равны. То есть треугольники A1CB1 и ACB подобны друг другу. Утверждение доказано.

Сторона АВ параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны АВ. Докажите, что DK — биссектриса угла ADC.

Решение.

Проведём FK параллельно AD (см. рисунок). Тогда AD = AK = KB. Следовательно, параллелограмм AKFD является ромбом. Диагональ DK ромба AKFD делит угол ADC пополам.

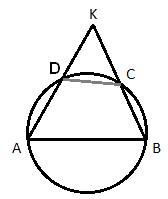
Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и ВС четырёхугольника пересекаются в точке К. Докажите, что треугольники KAB и KCD подобны.

Решение.

Если вокруг четырехугольника можно описать окружность, то суммы его противоположных углов равны по 180 градусов, то есть 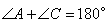 . Если положить угол  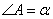, тогда угол  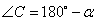, и, учитывая, что углы  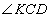 и 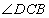  смежные, то угол

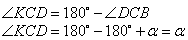
то есть он равен углу  . Таким образом, треугольники KAB и KDC подобны по двум углам (угол K – общий). Утверждение доказано.

В остроугольном треугольнике ABC проведены высоты BB1 и CC1 Докажите, что углы BB1C1 и ВСC1 равны.

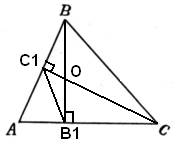
Решение.

1. Из рисунка видно, что треугольники BOC1 и CB1O подобны по двум углам (углы 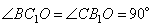 , так как CC1 и BB1 – высоты, а углы  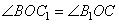 как вертикальные углы). В подобных треугольниках соответственные стороны пропорциональны, то есть можно написать соотношение

.

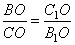2. Треугольники C1OB1 и BOC подобны по двум пропорциональным сторонам и углам между ними (углы 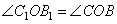  – вертикальные).

3. Из подобия треугольников следует равенство углов:

,

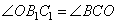а, значит, равны и углы

.

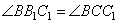В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О. Докажите, что площади треугольников АОВ и COD равны.

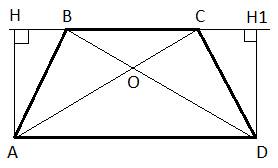
Решение.

Запишем площадь треугольника ABO в виде:

,

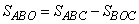где 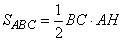  - площадь треугольника ABC;  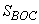 - площадь треугольника BOC. То есть площадь треугольника ABO можно представить как:

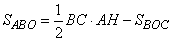.  (1)

Аналогично запишем площадь треугольника DCO, имеем:

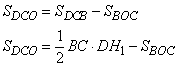
Так как 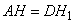 , то последнее выражение можно переписать в виде:

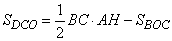.  (2)

Выражения (1) и (2) идентичны между собой и описывают площади треугольников ABO и DCO, то есть площади этих треугольников равны. Утверждение доказано.

Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.

Решение.

Треугольник CEF равен треугольнику DEF по трем сторонам, т.к. CE=DE (как радиусы одной окружности), EF – общая сторона (см. рисунок ниже). Тогда углы  .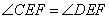

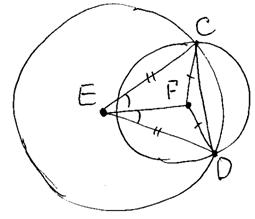
Рассмотрим треугольник CED – равнобедренный, EF – биссектриса угла E, следовательно, EF – высота и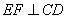 

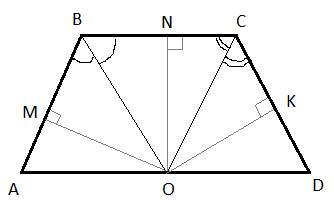
Биссектрисы углов B и C трапеции ABCD пересекаются в точке О, лежащей на стороне AD. Докажите, что точка О равноудалена от прямых АВ, ВС и CD.

Решение.

По условию задачи ABCD – трапеция с основаниями BC и AD и биссектрисами BO и CO, то есть углы 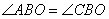  и 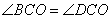 . Из точки O проведем три перпендикуляра  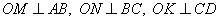 (по сути они будут являться расстояниями от точки O до прямых AB, BC и CD).

Теперь заметим, что треугольники BMO=BNO равны как прямоугольные по гипотенузе и острому углу: BO – общая гипотенуза; 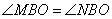 , так как BO – биссектриса. Из равенства треугольников следует, что OM=ON.

Аналогично для треугольников CNO=CKO, которые равны как прямоугольные по гипотенузе и острому углу: CO – общая гипотенуза; 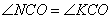 , так как CO – биссектриса. Следовательно, ON=OK.

Таким образом, имеем, что MO=NO=KO, а значит, точка O равноудалена от прямых AB, BC и CD. Положение доказано.

Внутри параллелограмма ABCD выбрали произвольную точку Е. Докажите, что сумма площадей треугольников АЕВ и CED равна половине площади параллелограмма.

Решение.

Проведем в параллелограмме ABCD высоту MN, равную h, и проходящую через точку E. Пусть расстояние ME=x, тогда NE=h-x. Площадь параллелограмма можно вычислить как

,

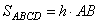а площади треугольников как

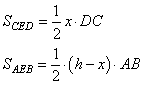
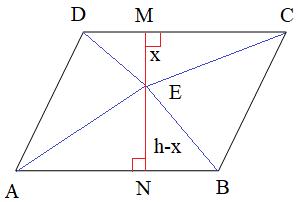
Так как в параллелограмме противоположные стороны равны, то AB=CD и сумма площадей треугольников равна

,

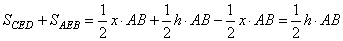что в точности равно половине площади параллелограмма ABCD. Утверждение доказано.

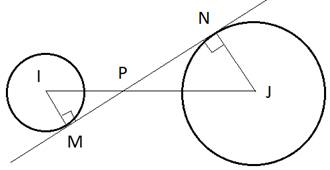
Окружности с центрами в точках I и J не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.

Решение.

По условию задачи прямые IP:JP=m:n, а MN – касательная к окружностям в точках M и N, следовательно, 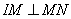  и 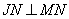 . Рассмотрим два прямоугольных треугольника IPM и JPN, которые подобны по двум углам: один угол у них прямой, а два других  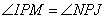 как вертикальные углы. Для подобных треугольников можно записать соотношение:

,

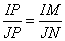но по условию 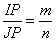 , следовательно,

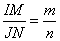
или, что эквивалентно, в виде

,

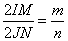где 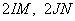  - диаметры соответствующих окружностей. Утверждение доказано.

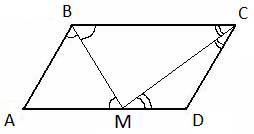
Биссектрисы углов В и С параллелограмма ABCD пересекаются в точке М стороны AD. Докажите, что М — середина AD.

Решение.

Так как ABCD – параллелограмм, то стороны 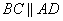  и 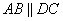 . Из этого положения следует равенство углов  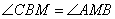 и 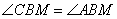 . Так как BM – биссектриса, то равны и углы  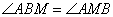. Из равенства двух углов при основании BM следует, что треугольник ABM – равнобедренный, с равными сторонами AB=AM. Аналогично для треугольника CMD, у которого углы при основании MC равны, следовательно, он равнобедренный и CD=MD. Учитывая, что ABCD – параллелограмм, у которого стороны AB=CD, то автоматически следует, что и AM=MD, то есть точка M – середина отрезка AD. Положение доказано.

На средней линии трапеции ABCD с основаниями AD и ВС выбрали произвольную точку Е. Докажите, что сумма площадей треугольников АЕВ и CED равна половине площади трапеции.

Решение.

Доказательство проведем от обратного. Докажем сначала, что сумма площадей треугольников BEC и AED составляет половину площади трапеции. Это же автоматические будет означать, что оставшаяся площадь (сумма площадей треугольников AEB и CED) также будет равна половине площади трапеции.

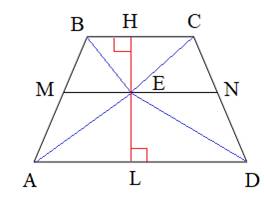
По условию задачи точка E лежит на отрезке MN – средней линии трапеции. Проведем через эту точку высоту HL трапеции. Тогда по определению средней линии, отрезки EH=EL=1/2∙HL. Используя данные обозначения, выразим площади треугольников BEC и AED следующим образом:

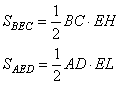
Соответственно, сумма этих площадей составит величину, равную

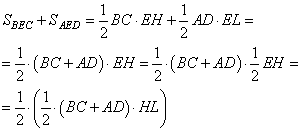
но так как 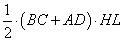  - это площадь всей трапеции, то получаем, что

.

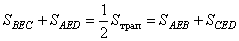Положение доказано.

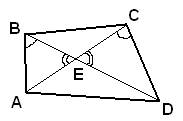
 В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

Решение.

Проведем в четырехугольнике диагонали AC и BD и отметим точку E на их пересечении. Рассмотрим треугольники ABE и DEC, у которых равны углы 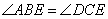  по условию задачи, а также равны углы  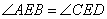 как вертикальные. Таким образом, треугольники ABE и DEC подобные по двум углам с пропорциональными сторонами BE и CE, а также AE и DE. Рассмотрим теперь треугольники AED и BEC, у которых сторона AE пропорциональна стороне DE, а сторона BE пропорциональна стороне CE, кроме того, равны углы  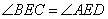 как вертикальные. Отсюда следует, что треугольники AED и BEC подобны по двум соответствующим пропорциональным сторонам и углу между ними. Так как у подобных треугольников соответствующие углы равны, то угол  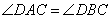. Утверждение доказано.

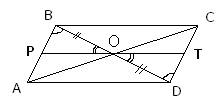
Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны АВ и CD в точках Р и Т соответственно. Докажите, что BP = DT.

Решение.

У параллелограмма диагонали BD и AC делятся в точке пересечения O пополам, то есть BO=OD. Кроме того, в параллелограмме противоположные стороны параллельны, то есть 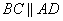  и, следовательно,  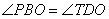 - как накрест лежащие при параллельных прямых и секущей BD. Углы  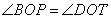 - как вертикальные углы. В результате имеем, что треугольники BOP и DOT равны по стороне и двум прилежащим к ней углам, а, следовательно, равны и стороны BP=DT.