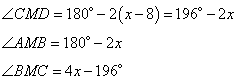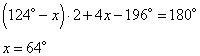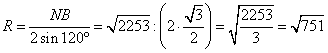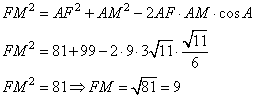Разбор 25 задания ОГЭ

В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 6:7, Прямая AK пересекает сторону ВС в точке Р. Найдите отношение площади треугольника BKP к площади треугольника ABK.

Решение.

Медиана KM разбивает треугольник AKC на два равновеликих треугольника — пусть их площади равны по 7S.

Поскольку 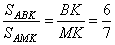 , получаем, что  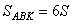. Пусть   и 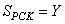 . Тогда  , отсюда  . Далее

тогда

,

то есть  . Получаем, что

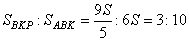
Ответ: 3:10

Биссектриса СМ треугольника ABC делит сторону АВ на отрезки AM = 9 и MB = 12. Касательная к описанной окружности треугольника ABC, проходящая через точку С, пересекает прямую АВ в точке D. Найдите CD.

Решение.

1. Так как CM – биссектриса, то по свойству биссектрисы:

,

откуда

.

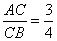2. Угол ABC – вписанный и опирается на дугу AC, поэтому, угол ABC в 2 раза меньше градусной меры дуги AC: 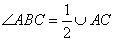  и  .

Угол ACD – это угол между касательной и хордой, следовательно,

И получаем, что 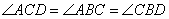 , а треугольники CDB и ADC подобны по двум углам (так как угол D – общий). Для подобных треугольников можно записать следующее отношение:

,

откуда

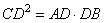 и  .

Так как AD = DB-21, имеем:

Ответ: 36.

В параллелограмме ABCD проведена диагональ АС. Точка О является центром окружности, вписанной в треугольник ABC. Расстояния от точки О до точки А и прямых AD и АС соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD.

Решение.

Окружность вписана в треугольник ABC с радиусами OM=ON=OP и перпендикулярными сторонам AB, BC, AC соответственно. По теореме об отрезках касательных, имеем:

MB=BN, AM=AP, CN=CP.

Пусть BM=BN=x, а CN=CP=y. Тогда BC=AD=x+y. Отрезок NN1=AH=17+7=24. Рассмотрим прямоугольный треугольник AMO. По теореме Пифагора найдем сторону AM:

Значит, AP=AM=24. Найдем величину x+y из формулы площади треугольника ABC:

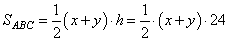
Эту же площадь можно вычислить как

,

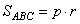где   - полупериметр треугольника ABC; r=7 – радиус вписанной окружности. Приравниваем площади, получаем уравнение:

Значит, BC=AD=33,6 и площадь параллелограмма, равна:

Ответ: 806,4

В трапеции ABCD основания AD и ВС равны соответственно 34 и 14, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой CD, если АВ=12.

Решение.

Продлим боковые стороны трапеции до пересечения в точке Р (см. рис.).

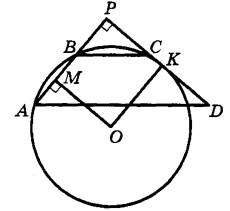
Из условия ясно, что  . Из подобия треугольников APD и ВРС получаем, что

,

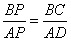то есть

откуда BP = 8,4.

Пусть окружность касается прямой CD в точке K, а O — её центр. Опустим из точки O перпендикуляр OM на хорду АВ. Точка М — середина АВ. Так как OMPK — прямоугольник, искомый радиус

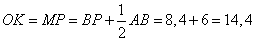
Ответ: 14,4.

На стороне ВС остроугольного треугольника ABC (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту AD в точке М, AD = 80, MD = 64, Н — точка пересечения высот треугольника ABC. Найдите АН.

Решение.

AD – высота треугольника ABC, значит,  . Учитывая, что MQ – хорда, с которой радиус окружности составляет 90º, то точка D делит MQ пополам и MD=DQ=64.

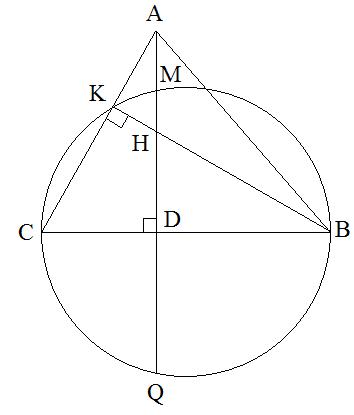
Следовательно,

AM = AD-MD = 80-64=16,

а

AQ = AD+DQ = 80+64 = 144

По следствию из теоремы о касательной и секущей, имеем:

Треугольники AKH и ADC подобны по двум углам:  , а угол CAD – общий. Следовательно,

откуда

Ответ: 28,8

В четырёхугольнике ABCD диагонали пересекаются в точке О под углом α. Точка F принадлежит отрезку АС. Известно, что ВО=10, DO = 14, АС = 18. Найдите AF, если площадь треугольника FBC в четыре раза меньше площади четырёхугольника ABCD.

Решение.

Площадь четырехугольника ABCD можно найти по формуле:

По условию задания

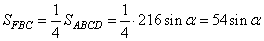    (1)

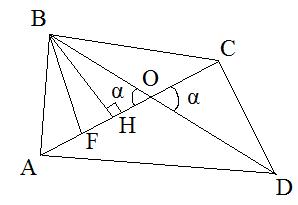
Площадь треугольника FBC также можно вычислить по формуле:

Пусть FC=x, тогда AF=18-x. Рассмотрим треугольник BHO, в котором BO=10,  , следовательно,  . Подставляем FC и BH в формулу площади треугольника FBC, имеем:

                 (2)

Приравнивая (1) и (2), получаем уравнение:

Следовательно, AF=18-10,8 = 7,2

Ответ: 7,2

Углы при одном из оснований трапеции равны 53° и 37°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 2. Найдите основания трапеции.

Решение.

По условию задания в трапеции ABCD углы при основании 53º и 37º, то есть,

Продлим стороны AB и CD до их пересечения в точке F. Получим треугольник AFD с углом

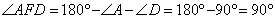
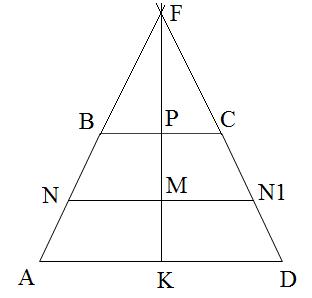
Имеем прямоугольный треугольник AFD, а также прямоугольный треугольник FBC, так как 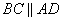  и углы:

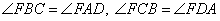
как соответственные при параллельных прямых. Пусть точка P – середина BC. Учитывая, что угол F=90º, имеем равные отрезки FP=BP=CP (как радиусы описанной окружности вокруг треугольника BFC). Аналогично для точки K – середины отрезка AD, имеем: FK=AK=KD.

По условию NN1 = 6 – средняя линия трапеции, значит, BC+AD=12 – в 2 раза больше средней линии. Следовательно, BP+AK=6. Далее, пусть FP=BP=x. Тогда FK=FP+PK=x+2 (PK=2 по условию задания). Следовательно, AK=x+2. Получаем уравнение:

Значит, BP=2, AK=4 и BC=2∙BP=4, AD=2∙AK=8.

Ответ: 4; 8.

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.

Решение.

В треугольнике ABC – BE биссектриса, а AD – медиана. Так как BE – биссектриса, то по свойству биссектрисы можно записать отношение: AB:BC = AE:EC. Но, так как по условию AB:BC = 1:2, то точка E делит отрезок AC в отношении AE:EC = 1:2. Далее, в треугольнике ABD BO – это и высота и биссектриса, значит, ABD – равнобедренный с AB=BD. И, так как, BD=DC (AD – медиана), то BC=2AB.

Треугольник AED – равнобедренный с AE=ED, так как  , точка O – середина AD (это следует из равнобедренности треугольника ABD). Следовательно, площади треугольников 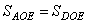 . Обозначим площадь  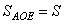, тогда

Пусть OE=x, тогда BO=96-x (так как BE=96 по условию задания). Из условия AD=96, имеем: AO=OD=96:2 = 48. Теперь, запишем площади треугольников по формулам:

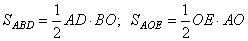
и, учитывая, что  , имеем:

Значит, OE=24, BO=96-24=72. Рассмотрим прямоугольный треугольник AOB, в котором гипотенуза AB, равна:

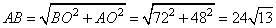
И, так как, BC=2AB, то BC=48√13. Рассмотрим прямоугольный треугольник AOE, в котором гипотенуза AE, равна:

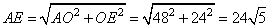
Значит, EC=48√5, AC=AE+EC = 72√5.

Ответ: 24√13, 48√13, 72√5.

 В треугольнике ABC известны длины сторон АВ = 28, АС = 56 , точка О — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите CD.

Решение.

Сделаем построение: из точки А проведем прямую через точку О и продолжим до точки А1. В результате АА1 – диаметр окружности, а углы   как вписанные, опирающиеся на диаметр.

Рассмотрим прямоугольный треугольник AA1B с прямым углом B из которого проведена высота BN. По свойству высоты BN, проведенной из прямого угла, можно записать равенство:

                         (1)

Рассмотрим подобные треугольники ADN и ACA1 (по двум углам: угол A1AC – общий и оба прямоугольные). Для них можно записать отношение:

        (2)

Объединяя равенства (1) и (2), получаем:

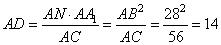
и

Ответ: 42.

Середина М стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 6, а углы В и С четырёхугольника равны соответственно 124° и 116°.

Решение.

В четырехугольнике ABCD точка M – середина AD и равноудалена от вершин A, B, C и D. Следовательно, AM=MD=MB=MC.

Пусть  , тогда  , так как треугольник AMB – равнобедренный с основанием AB. Также

поэтому

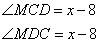
Учитывая, что сумма углов в любом треугольнике 180 градусов, имеем:

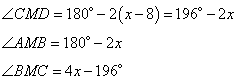
Рассмотрим треугольник BMC, в котором сумма углов равна

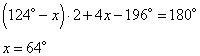
Следовательно,

и треугольник BMC – равносторонний. Поэтому BM=BC=6 и AM=BM=6. Тогда сторона AD=2AM=2∙6=12.

Ответ: 12.

В трапеции ABCD боковая сторона АВ перпендикулярна основанию ВС. Окружность проходит через точки С и D и касается прямой АВ в точке Е. Найдите расстояние от точки Е до прямой CD, если, AD = 4, ВС = 2.

Решение.

Продлим стороны AB и CD так, чтобы они пересеклись в точке T. Пусть  . По условию задания BC=2, AD=4, следовательно,

QD = AD-BC = 4-2 = 2

Из прямоугольного треугольника QCD, имеем:

Тот же самый угол можно выразить и так:

А, учитывая, что  , можно записать отношение:

Далее, так как TE – касательная к окружности (по условию задания), а TD – секущая, то по теореме о касательной и секущей, имеем:

Треугольники TPE и TAD подобны по двум углам: 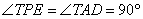 , угол T – общий. Значит, 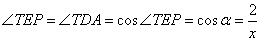. Следовательно,

Ответ: 2√2.

Окружности радиусов 12 и 20 касаются внешним образом. Точки А и В лежат на первой окружности, точки С и D — на второй. При этом АС и BD — общие касательные окружностей. Найдите расстояние между прямыми АВ и CD.

Решение.

Так как AC и BD – касательные, то 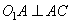 ,  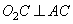. Также   (так как ACPO1 – прямоугольник), следовательно, PO2=20-12=8, так как AO1=12, CO2=20. А расстояние между центрами окружностей O1O2=12+20=32.

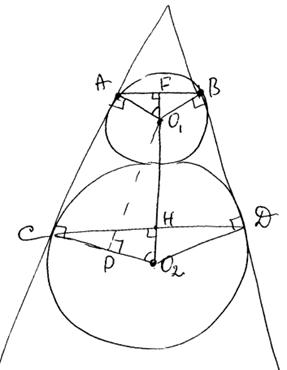
Рассмотрим прямоугольный треугольник O1PO2, из которого имеем:

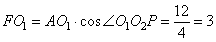Углы  , так как они соответственные. Рассмотрим прямоугольный треугольник AFO1, в котором  , следовательно,  . Из прямоугольного треугольника CHO2 по аналогии, получаем:  . Таким образом, расстояние между прямыми AB и CD, равно:

Ответ: 30.

В треугольнике ABC биссектриса угла А делит высоту, проведённую из вершины В, в отношении 5 : 4, считая от точки В. Найдите радиус окружности, описанной около треугольника ABC, если ВС = 12.

Решение.

По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5,  но AH:AB – это косинус угла A, то есть  . Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим

.

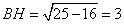Тогда синус угла A равен 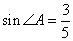 . По следствию теоремы синусов имеем:

,

где R – радиус описанной окружности. Следовательно,

.

Ответ: 10.

Четырёхугольник ABCD со сторонами АВ=11 и CD = 41 вписан в окружность. Диагонали АС и BD пересекаются в точке К, причём угол AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Решение.

Углы   как вертикальные. Проведем отрезок DN параллельный отрезку AC. В этом случае 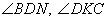  - накрест лежащие при параллельных прямых AC и DN и секущей BD.

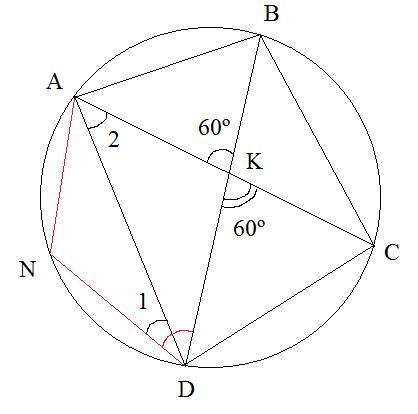
Четырехугольник DNAB вписан в окружность, следовательно,

откуда

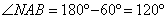
Далее,   как накрест лежащие при параллельных прямых AC, DN и секущей AD, следовательно, дуга AN равна дуге DC, откуда AN=DC=30.

Рассмотрим треугольник NAB вписанный в окружность. По теореме косинусов, имеем:

По теореме синусов можно записать:

,

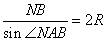где R – радиус описанной окружности. Из последнего выражения:

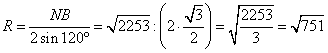
Ответ: √751

Боковые стороны АВ и CD трапеции ABCD равны соответственно 16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны АВ. Найдите площадь трапеции.

Решение.

Пусть М — середина АВ (см. рис.). Продолжим биссектрису DM угла ADC до пересечения с продолжением основания ВС в точке K. Поскольку 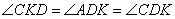 , треугольник KCD — равнобедренный, KC = CD = 34. Тогда KB = КС - ВС = 34 - 2 = 32.

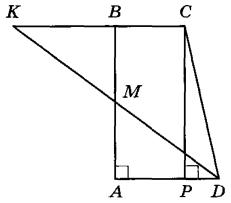
Из равенства треугольников AMD и ВМК следует, что AD = BK = 32. Проведём через вершину C прямую, параллельную стороне AB, до пересечения с основанием AD в точке P. Треугольник CPD — прямоугольный, так как

Поэтому CP — высота трапеции. Следовательно,

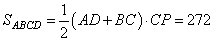
Ответ: 272.

Медиана ВМ треугольника ABC является диаметром окружности, проходящей через середину отрезка ВС. Найдите длину стороны АС, если радиус окружности, описанной около треугольника ABC, равен 11.

Решение.

Окружность проходит через точку F с диаметром BM (где BM – медиана треугольника ABC). Следовательно, точка M – точка касания, а AC – касательная к малой окружности. Отсюда получаем, что   и треугольник BAM – равнобедренный с AB=BC, BM – биссектриса угла B.

Точка O – центр окружности и середина отрезка BM. Точка F – середина отрезка BC, значит, OF – средняя линия треугольника BMC и  . Треугольник BOF – равнобедренный, следовательно, углы 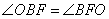  и с учетом  , имеем:  , значит, треугольник BMC – прямоугольный и равнобедренный с BM=MC. В таком треугольнике углы при основании равны по 45º:  . И, так как BM – биссектриса угла B, получаем, что 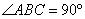 . Треугольник ABC может иметь угол B=90º только при условии, что AC – диаметр большой окружности, описанной вокруг треугольника ABC.

По условию задания радиус описанной окружности равен R=11, значит,

Ответ: 22

Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если ВС = 6, а расстояние от точки K до стороны АВ равно 6.

Решение.

Так как ABCD параллелограмм, а AK и BK – биссектрисы углов A и B, то точка K равноудалена от сторон AB и BC (см. рисунок). По условию задачи точка K удалена от стороны AB на расстояние 6 единиц, следовательно, от стороны BC она также удалена на 6 единиц. Получаем, что высота параллелограмма (красная линия на рисунке) равна 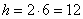  единиц. Тогда площадь параллелограмма можно найти как

.

Ответ: 72.

Точки М и N лежат на стороне АС треугольника ABC на расстояниях соответственно 9 и 11 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если  .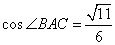

Решение.

1. Треугольник AFM подобен треугольнику ANF по двум углам (угол A – общий, а  ). Отсюда следует, что

2. Рассмотрим треугольник AFM. По теореме косинусов находим FM:

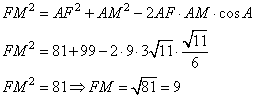
То есть, треугольник AFM – равнобедренный с основанием AF. Соответственно, углы при основании такого треугольника равны, получаем,  , откуда

и  .

3. Рассмотрим треугольник FMN. По теореме синусов, имеем:

,

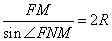где R – радиус описанной окружности. Откуда:

.

Ответ: 5,4.