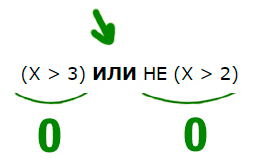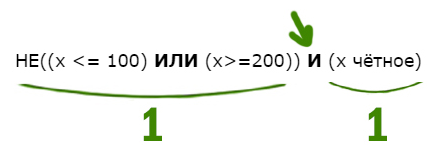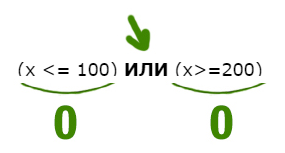Разбор 3 задания ОГЭ по информатике

Определять истинность составного высказывания

Определение истинности составного высказывания в логике является важным аспектом для анализа и оценки утверждений, которые содержат несколько условий или утверждений. Составные высказывания могут быть объединены с использованием различных логических операторов, таких как «И» (конъюнкция), «ИЛИ» (дизъюнкция), «НЕ» (отрицание) и другие. Чтобы определить истинность составного высказывания, следует учитывать следующие аспекты:

1. Знание логических операторов: Первым шагом является понимание логических операторов и их значения. Например, оператор «И» (конъюнкция) возвращает истинное значение только в том случае, если оба условия истинны. Оператор «ИЛИ» (дизъюнкция) возвращает истинное значение, если хотя бы одно из условий истинно. Оператор «НЕ» (отрицание) инвертирует значение условия.

2. Оценка условий: Далее, необходимо оценить каждое из условий, входящих в составное высказывание. Это может включать в себя сравнение значений, вычисления и проверку различных условий.

3. Применение логических операторов: Используя значения каждого условия и логические операторы, вычисляйте истинность всего составного высказывания. Это может потребовать комбинирования нескольких условий с учетом операторов.

4. Проверка результатов: После вычисления, проверьте окончательное значение составного высказывания. Если оно истинное, то всё составное высказывание считается истинным; в противном случае оно считается ложным.

Пример:

Пусть у нас есть составное высказывание «A И B», где A и B — отдельные условия.

• Если A = true и B = true, то «A И B» будет истинным.

• Если A = false и B = true или A = true и B = false, то «A И B» будет ложным.

Точно так же можно определить истинность для более сложных составных высказываний.

Важно заметить, что правильное определение истинности составного высказывания является фундаментальным вопросом в математике и логике, и оно играет важную роль в решении логических задач и разработке программ, особенно в компьютерных науках.

Разбор 3 задания ОГЭ

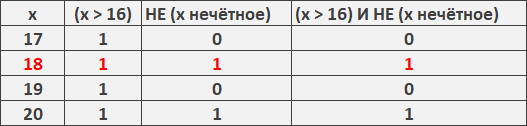
Напишите наименьшее натуральное число x, для которого истинно высказывание:
(x 16) И НЕ (x нечётное).

Для данного высказывания «x 16 И НЕ (x нечётное)» наименьшим натуральным числом, которое удовлетворяет этому условию, будет x = 18.

Давайте проверим:

1. x 16: 18 16 — это истинное условие.

2. x нечётное: 18 — четное число, поэтому «x нечётное» — ложное условие.

3. Истинно И НЕ ложно = истинно.

Таким образом, при x = 18 высказывание «x 16 И НЕ (x нечётное)» истинно.

Задача 2

Напишите наибольшее целое число x, для которого истинно высказывание:
НЕ (X И НЕ (X = 11)

Решение:

Опять высказывание должно быть истинным.

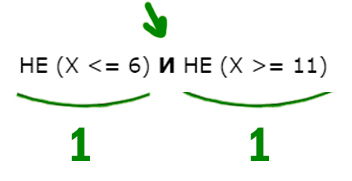
С одной стороны X должен быть НЕ меньше или равно 6, т.е значит, X нужно взять больше 6 (X 6). Причём само число 6 не входит в этот диапазон.

С другой стороны X НЕ больше или равно 11, т.е. X должен быть меньше 11 (X

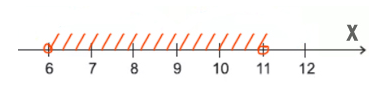
Наибольшее целое число будет 10.

Ответ: 10

Задача 3 Союз И

Напишите наименьшее натуральное двузначное число, для которого истинно высказывание:
НЕ (первая цифра нечётная) И (число делится на 3)

Решение:

Высказывание должно быть истинным.

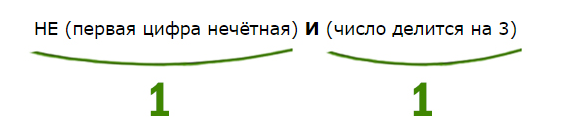
Первая цифра должна быть НЕ нечётная. Значит, она должна быть чётная. Число должно делится на 3. Найдём наименьшее двухзначное число, у которого первая цифра чётная, и оно делится на 3. Это будет 21.

Ответ: 21

Задача 4 Союз ИЛИ

Для какого целого числа X ЛОЖНО высказывание: (X 3) ИЛИ НЕ (X 2)

Решение:

В этой задаче используется союз ИЛИ. Нужно, чтобы высказывание было ложным. Ложь при союзе ИЛИ получается только в одном случае, когда слева и справа стоят нули.

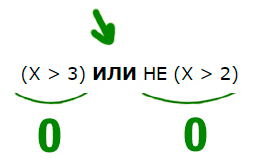
Утверждение, что X 3 должно быть ложно, значит, если его перевернуть, получится X 2) тоже должно быть ложно. Значит, если перевернём это утверждение, частицу НЕ нужно убрать. Получается просто X 2.

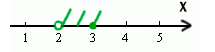
Получается, что только одно целое число входит в допустимый диапазон. Это тройка.
Ответ: 3

Задача 5 Частица НЕ над всем выражением

Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((xИЛИ (x Решение:

Нам нужно сделать выражение истинным. Но всё выражение находится под влиянием частицы НЕ. Можно эту частицу полностью убрать, но воспринимать, как будто нужно сделать выражение ложным. А дальше всё как обычно.

Ложь у союза ИЛИ получается в одном случае.

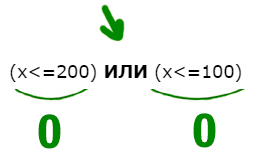
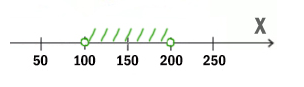
Первое выражение выдаёт ноль, когда x200 (равно 200 не входит). Второе выражение выдаёт ноль, когда x100. Объединив эти два условия получаем:

x 200

Наименьшее число получается 201.

Ответ: 201

Задача 6

Напишите наименьшее натуральное число x, для которого истинно высказывание:
НЕ((x ИЛИ (x=200)) И (x чётное)

Решение:

В этой примерной задаче из ОГЭ по информатике применим все приёмы, которые мы разбирали до этого.

Когда союз И выдаёт единицу ?

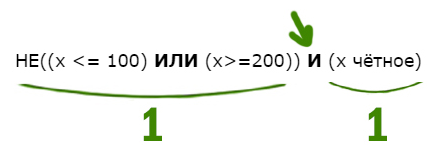
Посмотрим, когда левое выражение выдаёт 1. Уберём частицу НЕ, но тогда будем смотреть, когда левое выражение выдаёт 0.

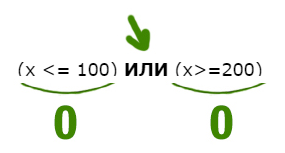
Перевернём оба выражения, которые находятся по обе стороны от союза ИЛИ. С одной стороны X100, с другой X

Учтём правое от союза И выражение. Наименьшее чётное число получается 102.
Ответ: 102