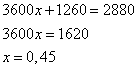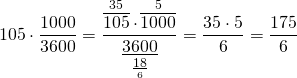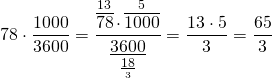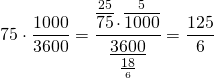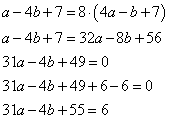Задача 21
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 80 км/ч и 40 км/ч. Длина пассажирского поезда равна 350 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 24 секундам. Ответ дайте в метрах.
Решение.
Обозначим через 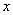 длину скорого поезда. Так как поезда движутся навстречу друг другу, то скорость прохождения поездов мимо друг друга составляет 80+40=120 км/ч. В задаче сказано, что поезда прошли мимо друг друга за 24 секунды (24/3600 часа). Это эквивалентно тому, что скорый поезд прошел за это время 350 метров (0,35 км) и еще свою длину. Получаем уравнение
длину скорого поезда. Так как поезда движутся навстречу друг другу, то скорость прохождения поездов мимо друг друга составляет 80+40=120 км/ч. В задаче сказано, что поезда прошли мимо друг друга за 24 секунды (24/3600 часа). Это эквивалентно тому, что скорый поезд прошел за это время 350 метров (0,35 км) и еще свою длину. Получаем уравнение
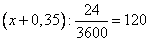
откуда имеем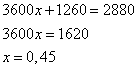
То есть длина скорого поезда 0,45 км или 450 метров. Ответ: 450.
Задача 1.
По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 40 км/ч. Длина пассажирского поезда равна 350 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского, равно 36 секундам. Ответ дайте в метрах.
Решение:
При движении навстречу друг другу скорость сближения поездов равна сумме их скоростей:
65+40=105 (км/ч) скорость сближения поездов
Переведём скорость из километров в час в метры в секунду:
105 км/ч=175/6 м/с
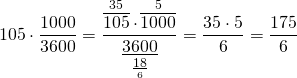
Скорый поезд прошел мимо пассажирского за 36 секунд. Умножим скорость сближения поездов на это время:
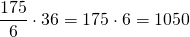
Длина поезда равна расстоянию от головы поезда до конца последнего вагона. 36 секунд — это время с момента, когда головной вагон скорого поезда поравнялся с головным вагоном пассажирского поезда, до момента, когда последний вагон скорого поезда проехал мимо последнего вагона пассажирского поезда.
Таким образом, 1050 м — это расстояние, между головным вагоном скорого поезда, и головным вагоном пассажирского поезда, то есть 1050 м — это сумма длин двух поездов.
Чтобы найти длину скорого поезда, из суммы длин вычитаем длину пассажирского поезда:
1050-350=700 м. Ответ: 700 метров.
Задача 2.
Поезд, двигаясь равномерно со скоростью 75 км/ч, проезжает мимо пешехода, идущего параллельно путям со скоростью 3 км/ч навстречу поезду, за 30 секунд. Найдите длину поезда в метрах.
Решение:
Так как пешеход идёт навстречу поезду, скорость сближения поезда и пешехода равна сумме их скоростей:
75+3=78 (км/ч) скорость сближения поезда и пешехода.
Скорость из км/ч переведём в м/с: 78 км/ч=65/3 м/с
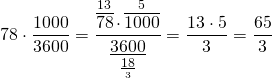
Умножим скорость сближения поезда и пешехода на время, за которое поезд проезжает мимо пешехода:
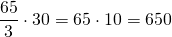 650 м — длина поезда. Ответ: 650 м.
650 м — длина поезда. Ответ: 650 м.
Задача 3
Поезд, двигаясь со скоростью 79 км/ч, проходит мимо идущего параллельно путям в том же направлении пешехода за 12 секунд. Определите длину поезда в метрах, если скорость пешехода равна 4 км/ч.
Решение:
Так как поезд и пешеход движутся в одном направлении (движение вдогонку), то скорость их сближения равна разности скоростей:
79-4=75 (км/ч) скорость сближения поезда и пешехода.
Переводим скорость из км/ч в м/с: 75 км/ч=125/6 м/с
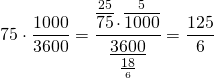
Умножим скорость сближения поезда и пешехода на время, за которое поезд проезжает мимо пешехода:
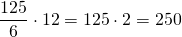
250 м — длина поезда. Ответ: 250 м
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Решение.
Пусть 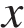 км — расстояние, которое проехал первый велосипедист до места встречи,
км — расстояние, которое проехал первый велосипедист до места встречи,  , тогда
, тогда 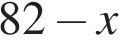 км — расстояние, которое проехал второй велосипедист до места встречи.
км — расстояние, которое проехал второй велосипедист до места встречи.
Составим таблицу по данным задачи:
|
| Скорость, км/ч | Время, ч | Расстояние, км |
| Первый велосипедист | 28 | 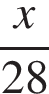
| 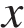
|
| Второй велосипедист | 10 | 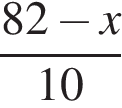
| 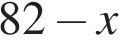
|
Так как первый велосипедист сделал остановку на  ч., составим уравнение:
ч., составим уравнение:
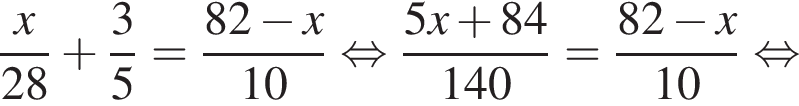
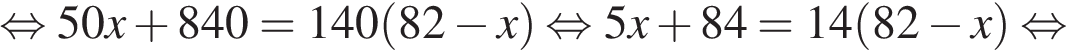
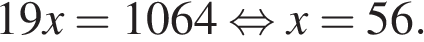
Таким образом, второй велосипедист проехал 82 − 56 = 26 км до места встречи.
Ответ: 26 км
№ 1 Расстояние между пристанями А и В равно 140 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 51 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
РЕШЕНИЕ:
v скорость плота 3км/ч
плот прошел 51 км
Время в пути 51 / 3 = 17 ч
v лодки х км/ч
по течению лодка прошла 140 / (х+3) ч
против течения лодка прошла 140 / (х-3) ч
На весь путь лодка потратила на один час меньше 16 часов
Составим и решим уравнение
__140__ + __ 140 __ = 16
х + 3 ________ х - 3
140(х-3) + 140 (х+3) = 16 (х+3)(х-3)
140 х + 140 х = 16 ( х ² - 9 )
280 х = 16 х² - 144
16 х ² - 280 х - 144 = 0
D = 280² - 4 ∙ 16 ∙ (-144) = 87 616 = 296 ²
х = 280 ± 296
____ 2 ∙ 16
х = 280 + 296
____ 32
х = 576
___ 32
х = 18
Ответ: 18
№ 2 Расстояние между пристанями А и В равно 48 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 25 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
РЕШЕНИЕ:
v плота 5км/ч
плот прошел 25 км
Время в пути 25 / 5 = 5 ч
v лодки х км/ч
по течению лодка прошла 48 / (х+5) ч
против течения лодка прошла 48 / (х-5) ч
На весь путь лодка потратила на один час меньше 4 часов
Составим и решим уравнение
__48__ + __ 48 __ = 4
х + 5 ________ х - 5
48(х-5) + 48 (х+5) = 4 (х+5)(х-5)
48 х + 48 х = 4 ( х ² - 25 )
96 х = 4 х² - 100
4 х ² - 96 х - 100 = 0
D = 96² - 4 ∙ 4 ∙ (-100) = 10 816 = 104 ²
х = 96 ± 104
____ 2 ∙ 4
х = 96 + 104
____ 8
х = 200
___ 8
х = 25
Ответ: 25
Задание 22. Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько требуется свежих фруктов для приготовления 21 кг высушенных фруктов?
Решение.
Пусть 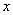 кг фруктов требуется для приготовления 21 кг высушенных фруктов. Так как в фруктах содержится 93% воды, то процент сухого вещества составляет 100-93=7%, и в x кг сухого вещества равно
кг фруктов требуется для приготовления 21 кг высушенных фруктов. Так как в фруктах содержится 93% воды, то процент сухого вещества составляет 100-93=7%, и в x кг сухого вещества равно
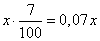 кг.
кг.
Масса сухого вещества в высушенных 21 кг фруктах составляет 100-16=84% и равна 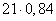 кг. По условию задачи величина
кг. По условию задачи величина 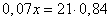 , откуда находим:
, откуда находим:
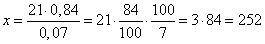 кг.
кг.
Ответ: 252.
Задание 22. Семь одинаковых рубашек дешевле куртки на 9 %. На сколько процентов десять таких же рубашек дороже куртки?
Решение.
Семь рубашек дешевле куртки на 9% означает, что 7 рубашек составляют 100-9=91% от стоимости куртки. Следовательно, одна рубашка – это 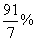 от стоимости куртки. Таким образом, 10 рубашек будут составлять
от стоимости куртки. Таким образом, 10 рубашек будут составлять 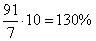 от стоимости куртки, т.е. будут на 30% дороже.
от стоимости куртки, т.е. будут на 30% дороже.
Ответ: 30.
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.
Решение.
Пусть 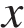 км/ч — скорость первого бегуна,
км/ч — скорость первого бегуна,  , тогда
, тогда  км/ч — скорость второго бегуна. Из условия известно, что второй бегун пробежал круг за
км/ч — скорость второго бегуна. Из условия известно, что второй бегун пробежал круг за 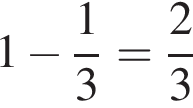 часа. При этом через час после старта первому бегуну оставался 1 км до окончания первого круга (расстояние в 1 км. — разность путей двух бегунов, пройденных одним за 1 ч., а другим за
часа. При этом через час после старта первому бегуну оставался 1 км до окончания первого круга (расстояние в 1 км. — разность путей двух бегунов, пройденных одним за 1 ч., а другим за  ч.). Составим уравнение:
ч.). Составим уравнение:
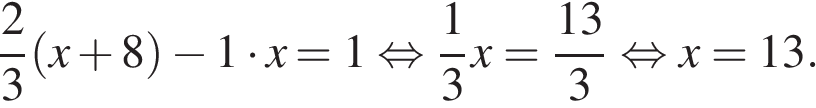
Таким образом, скорость первого бегуна равна 13 км/ч.
Ответ: 13 км/ч.
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 15 минут назад. Найдите скорость первого бегуна, если известно, что она на 6 км/ч меньше скорости второго.
Решение.
Пусть 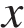 км/ч — скорость первого бегуна, тогда
км/ч — скорость первого бегуна, тогда  км/ч — скорость второго бегуна. Из условия известно, что второй бегун пробежал круг за
км/ч — скорость второго бегуна. Из условия известно, что второй бегун пробежал круг за 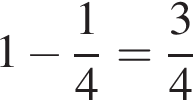 часа, при этом через час после старта первому бегуну оставался 1 км до окончания первого круга, составим уравнение:
часа, при этом через час после старта первому бегуну оставался 1 км до окончания первого круга, составим уравнение:
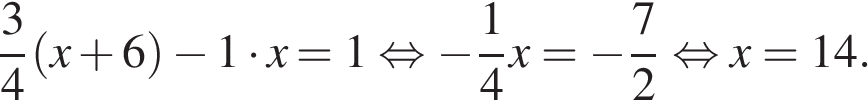
Таким образом, скорость первого бегуна равна 14 км/ч.
Ответ: 14.
Задача
Два автомобиля одновременно отправляются в 930-километровый пробег. Первый едет со скоростью, на 31 км/ч больше, чем второй, и прибывает к финишу на 5 часов раньше второго. Найдите скорость первого автомобиля.
Пусть х км/ч - скорость второго автомобиля, тогда х+31 км/ч - скорость первого автомобиля. Следовательно 930/х - время, которое затратил на дорогу второй автомобиль, а 930/(х+31) - время второго. (Самое важное в этой задаче понять, кто затратил на дорогу больше времени, т.е из чего что вычитать. Т.к. скорость первого больше, то он прибыл раньше, чем второй (на 5 часов))
1) 930/х - 930/(х+31) = 5 (Дальше приводим к общему знаменателю)
х^2 + 31х - 5766 = 0
D = 155^2
х1 = -93 (посторонний корень)
х2 = 62 (км/ч0 - скорость второго автомобиля.
2) 62 + 31 = 93 (км/ч) - скорость первого автомобиля.
Ответ: 93 км/ч
.Задание 21. Найдите значение выражения 31a-4b+55, если 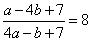
Решение.
Преобразуем выражение 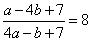 , получим:
, получим:
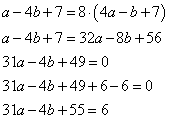
Ответ: 6.