Разновидности симметрии

МБОУ ЧР «Ишлейская СОШ» Минобразования Чувашии(Муниципальное бюджетное учреждение Чувашской Республики «Ишлейская средняя общеобразовательная школа)

ПРОЕКТ ПО МАТЕМАТИКЕ:

Разновидности симметрии

Работу выполнила: Яруткина Т.С.

Ученица 9а класса, МБОУ «ИСОШ»

Руководитель: Ильина Галина Геннадиевна,

учитель по математике МБОУ «Ишлейская СОШ»

Ишлеи 2021

1

Содержание:

1. Введение----------------------------------------------3

2. Актуальность---------------------------------------3

3. Проблема---------------------------------------------3

4. Цель----------------------------------------------------3

5. Задачи-------------------------------------------------3

6. Понятия «симметрия» и «асимметрия»-----4

7. Методы исследования----------------------------5

8. Заключение------------------------------------------9

9. Литература-----------------------------------------10

2

Введение

• Симметрия считается фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений. В давние времена слово «симметрия» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей». С симметрией мы встречаемся всюду. Понятие «симметрии» проходит через всю многовековую историю человеческого творчества. Главные принципы симметрии такие: как гармония, соразмерность, неизменность играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке.

Актуальность: Симметрия окружает человека, находя своё проявление как в живой, так и в неживой природе. Объяснение законов симметрии важно для понимания красоты, гармонии, жизни.

Проблема: Какое значение имеет в нашей жизни симметрия?

Цель: Изучить шире понятия симметрия и асимметрия.

Задачи:

• Рассмотреть симметрию плоских фигур;

• Рассмотреть симметрию у животных;

• Значение симметрии в познании природы;

• Взаимосвязь симметрии и асимметрии

3

Что же такое симметрия?

Симметрия — в широком смысле это соответствие, неизменность; основополагающий принцип самоорганизации материальных форм в природе и формообразования в искусстве. Отсутствие или нарушение симметрии называется асимметрией.

Существует две группы симметрий:

• Первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.

• Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира ее можно назвать физической симметрией.

• Асимметрия — противоположность симметрии, отражающая существующее в объективном мире нарушение порядка, равновесия, относительной устойчивости, пропорциональности. Это столь же существенный момент законов сохранения как и симметрия. Является основой существования связи между законами.

4

Виды исследования:

• Симметрия плоских фигур. Зеркальная симметрия. Геометрическая фигура называется симметричной относительно плоскости S, если для каждой точки E этой фигуры может быть найдена точка E’ этой же фигуры, так что отрезок EE’ перпендикулярен плоскости S и делится этой плоскости пополам (EA=AE’). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу вузком смысле слова. Они называются зеркально равными.

• Центральная симметрия. Геометрическая фигура (или тело) называется симметричной относительно центра C, если для каждой точки A этой фигуры может быть найдена точка E этой же фигуры, так что отрезок AE проходит через центр C и делится в этой точке пополам (AC=CE). Точка C называется центром симметрии.

• Симметрия вращения. Тело (фигура) обладает симметрией вращения, если при повороте на угол 360 градусов/n (здесь n – целое число) вокруг некоторой прямой AB (оси симметрии) оно полностью совпадает со своим начальным положением. При n=2 мы имеем осевую симметрию. Треугольники имеют также осевую симметрию.

• Примеры вышеупомянутых видов симметрии: шар (сфера) обладает и центральной, и зеркальной, и симметрией вращения. Центром симметрии является центр шара; плоскостью симметрии является плоскость любого большого круга; осью симметрии – ось конуса. Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.

5

• Симметрия плоских фигур. Зеркально – осевая симметрия. Если плоская фигура ABCDE симметрична относительно плоскости S (что возможно, если только плоская фигура перпендикулярна плоскости S), то прямая KL, по которой эти плоскости пересекаются, является осью симметрии второго порядка фигуры ABCDE. В этом случае ABCDE называется зеркально-симметричной.

• Центральная симметрия. Если плоская фигура имеет ось симметрии второго порядка, перпендикулярную плоскости фигуры (прямая ABCDEF), то точка O, в которой пересекаются прямая MN и плоскость фигуры ABCDEF, является центром симметрии.

6

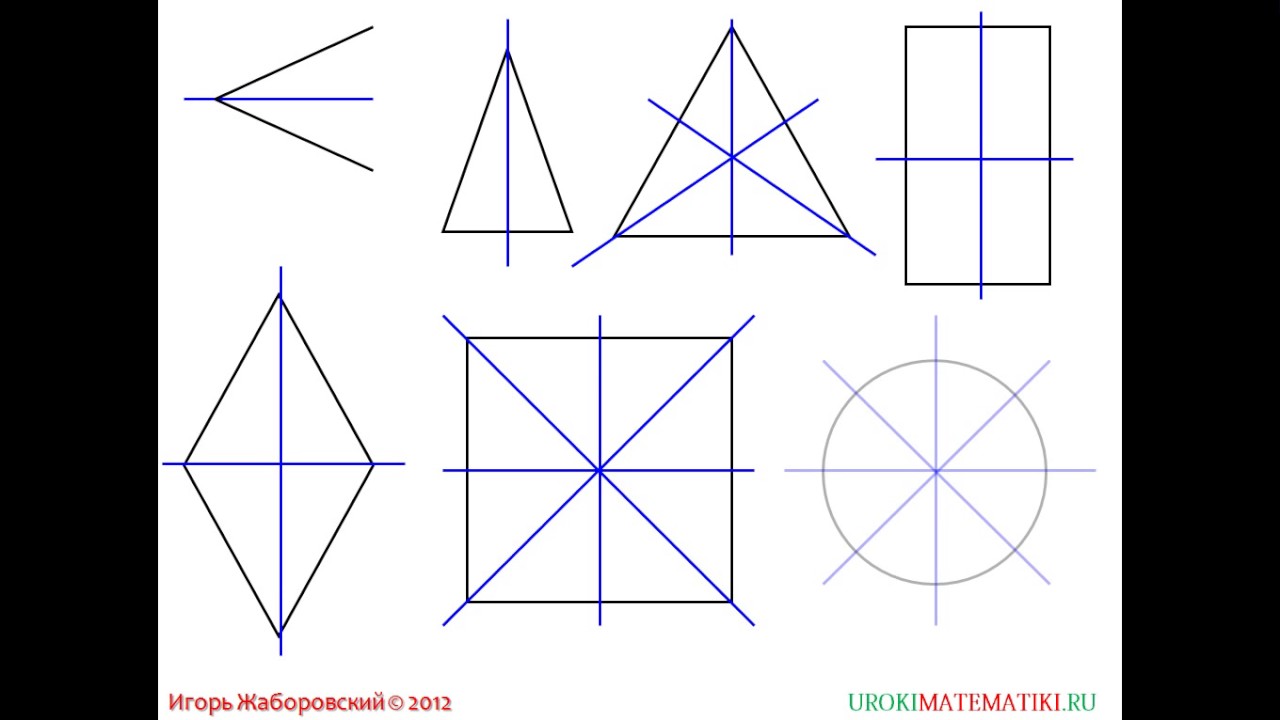
• Примеры симметрии плоских фигур: параллелограмм имеет только центральную симметрию. Его центр – точка пересечения диагоналей. Равнобочная трапеция имеет только осевую симметрию. Ее ось симметрии – перпендикуляр, проведенный через середины оснований трапеции. Ромб имеет и центральную, и осевую симметрию. Его ось симметрии – любая из его диагоналей; центр симметрии точка их пересечения.

• Симметрия у животных. Прекрасный пример радиально-лучевой симметрии дают радиолярии. Кишечнополостным, как сидячим, так и пелагическим (медузы), свойственна радиально-лучевая симметрия, при которой сходственные части расположены вокруг оси вращения, причем эта симметрия может быть самого различного порядка в зависимости от того, на какой угол следует повернуть тело животного, чтобы новое положение совпало с исходным. Таким образом. Может получаться 4-,5-,8-лучевая симметрия и более, до симметрии порядка бесконечности. Наблюдая хаотическую россыпь звезд на ночном небе, мы понимаем, что за внешним хаосом скрываются вполне симметричные спиральные структуры галактик, а в них – симметричные структуры планетных систем. Симметрия внешней формы кристалла является следствием ее внутренней симметрии – упорядоченного взаимного расположения в пространстве атомов (молекул). Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомом, так называемой кристаллической решетки.

• Видный советский ученый академик В.И. Вернадский писал в 1927 году: “Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности”. Симметрия устанавливает внутренние связи между объектами и явлениями, которые внешне никак не связаны. 7

• Винтовая симметрия — это симметрия объекта относительно группы преобразований, являющихся композицией преобразования поворота объекта вокруг оси и переноса его вдоль этой оси.

• По строению группы преобразований винтовая симметрия разделяется на:

1.Бесконечную винтовую симметрию

2.Винтовую симметрию n-го порядка

3.Неповторяющуюся винтовую симметрию

Спиральная симметрия в искусстве встречается в чистом виде мало, в основном она присутствует в узорах, изредка – в архитектуре (винтовые лестницы, витые колонны), графическом дизайне. Её изобразительная особенность состоит в поступательном движении точки, линии, плоскости, формы с постоянной угловой скоростью вдоль неподвижной осевой линии. Этот тип симметрии с успехом может применяться в разработке фирменных знаков.

8

Заключение:

Таким образом, симметричные фигуры мы встречаем в космосе, на земле: среди растений, животного мира, в горных породах, в моряках и океанах.. Можно выделить два случая наложения симметрии среды на симметрию формирующего в ней тела:

1. Все элементы собственной симметрии тела совпадают с элементами симметрии среды;

2. Элементы собственной симметрии тела лишь частично совпадают с элементами симметрии среды.

Мы узнали, что кроме изученных нами в школе центральной осевой симметрии, бывает зеркальная симметрия, симметрия вращения, симметрия плоских фигур, билатеральная симметрии, радиально-лучевая симметрия, шаровая симметрия, симметрия подобия, «бесконечная симметрия». Можно сказать, что симметрия и асимметрия – это две формы проявления одной и той же закономерности – закономерности двойственности.

9

Список литературы:

1. Шубников А.В., Копцик В.А. “Симметрия в науке и искусстве” Москва, 1972г.

2. И.Я. Депман, И.Я. Виленкин. За страницами учебника. Пособие для учащихся 5-6 классов. Москва. “Просвещение” 1989г.

3. И.И. Шафрановский. Симметрия в природе.

4. Энциклопедический словарь юного математика для среднего и старшего школьного возраста. Москва. “Педагогика” 1989г.

5. Урманцев Ю.А. “Cимметрия природы и природа симметрии” Москва, Мысль, 1974г.

10