Муниципальное бюджетное общеобразовательное учреждение
Молотицкая средняя общеобразовательная школа
Разновозрастное занятие по математике
в 7,9 классах в рамках тематического дня
«Экскурсия в математику»
Учитель
Л.В.Чернышова
2013
Экскурсия в математику
Разновозрастное занятие по математике в 7,9 классах
Цели занятия:
Научить применять знания, полученные на уроках, в нестандартных ситуациях, познакомить с разными приемами решения задач.
Развивать коммуникативные способности учащихся;
Развивать умение сравнивать, анализировать, делать вывод
Развивать логическое мышление, смысловую и образную память
Ход занятия
| Этап | Цель этапа | Деятельность учителя | Деятельность учеников |
| 7 класс | 9 класс |
| 1. Орг момент | Создать положительную мотивацию к деятельности на уроке | Учитель использует ярку дминанту для начала урока (приложение 1) | Пытаются найти ответ к уравнению, решение которого откладывается до конца занятия |
| 2. Развиваем гибкость ума через решение задач | 7 класс. научить применять переформулировки условия задачи или переключаться с прямого хода мыслей на обратный 9 класс. отрабатать навыки расширения сферы поиска решения, учиться отделять главное от второстепенного, извлекать из текста не только то, что там сказано прямо, но и то, что содержится между строк.
| Предлагает задания (приложение 2) | Работают в группах
| Работают в группах |
| Обсуждается решение задач |
| 3. Ситуации в жизни такие: либо сложные, либо простые.
| 7 класс. учиться видеть главные причины происходящего, объяснять их сущность, делать выводы, находить закономерности, отрабатывать вычислительные навыки. 9 класс. Развивать интеллектуальные особенности учащихся через применение на уроках различных нестандартных и олимпиадных задач, что позволяет развивать творческое мышление, повышать математические способности учащихся. | Предлагает задания, комментирует , направляет по ходу решения (приложение 3) | Работают в группах
| Работают в группах |
| Обсуждается решение задач |
| 4. Без логики нет математики | Отрабатать навыки размышления над задачей, учиться отделять главное от второстепенного, вычленять ведущие закономерности явлений. Такие задачи носят занимательный характер, решение которых развивает логическое мышление и не требуют большого запаса математических знаний, поэтому они привлекают даже тех учащихся, которые не очень любят математику.
| Предлагает задания, комментирует , направляет по ходу решения (приложение 4) | Работают в группах
| Работают в группах |
| Обсуждается решение задач |
| 5. В геометрию тропинки одолеем без запинки | Учиться проводить необходимые дополнительные построения, переводить текст задачи на язык математики
| Предлагает задания, комментирует , направляет по ходу решения (приложение 5) | Работают в группах
| Работают в группах |
| Обсуждается решение задач |
| 6. итог занятия | Найти решение уравнения, предложенного в начале урока | Нацеливает на решение уравнения нестандартным способом, предлагает «выйти за рамки» текста задачи | Совместно решают уравнение |
| 7 Рефлексия | Подвести итоги занятия, определить достижение цели каждым учеником | Рефлексия (приложение 6) |
ПРИЛОЖЕНИЕ 1
Оформление доски.
Эмблема урока: 28k + 30n + 31m = 365
Комментарий учителя к уравнению:
Говорят уравнение вызывает сомнение, но итогом сомнения может быть озарение!
Задание для учащихся. Найти хотя бы одно решение уравнения.
(Уравнение, красочно оформленное, вывешивается сверху, в центре доски, к концу урока будет найдено его решение).
ПРИЛОЖЕНИЕ 2
II этап. Развиваем гибкость ума через решение задач.
7 класс. .
1) У двух зрячих один брат слепой, но у слепого нет зрячих братьев. Как это может быть? (из первой фразы как будто следует, что речь в задаче идет о братьях, тогда как на самом деле зрячими оказываются сестры).
2) Дано 5 спичек. Сложите их них 2 равносторонних треугольника. А теперь сложите из 6 спичек – 4 равносторонних треугольника (первая задача решается в плоскости, а вторая в пространстве).
9 класс.
1) Известно, что бумеранг можно бросить так, что он вернется обратно. А можно как-то ухитриться и бросить теннисный мяч так, чтобы он вернулся обратно?
Ответ: мяч нужно бросить вверх и он вернется обратно.
2) В лесной школе после первой контрольной по математике животные получили следующие отметки:
ЕНОТ – “1”, БАРСУК –“2”, КОЗЕРОГ– “3”, ОБЕЗЬЯНА – “4”.
А сколько получила корова?
Ответ: корова получила “5”, нужно подсчитать количество замкнутых линий в буквах.
ПРИЛОЖЕНИЕ 3
7 класс
Решить задачу: Можно ли найти 7 таких последовательно натуральных чисел, что их сумма будет простым числом?
Ответ: нет.
Учащиеся решали задание из учебника, в котором требуется найти пропущенные числа:
У них получились разные ответы:
| 26 | 26 | 52 | | 19 | 26 | 52 |
| 11 | 33 | 44 | 11 | 18 | 44 |
Найдите правила, по которым учащиеся заполнили клетки.
9 класс.
Что больше? 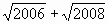 или 2
или 2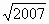
Ответ: 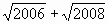
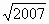
Найти два числа, если их сумма, произведение и частное от деления равны между собой, то есть а + b = а · b = а : b
Ответ: а =  ; b = –1
; b = –1
ПРИЛОЖЕНИЕ 4
7 класс. В трех мешках находится крупа, вермишель и сахар. На одном мешке написано “крупа”, на другом “вермишель”, на третьем “крупа или сахар”. В каком мешке что находится, если содержимое каждого для них не соответствует действительности?
9 класс. На столе стоят три одинаковые коробки, в одной находятся 2 желтых шара, в другом – один красный и один желтый, в третьем 2 красных. На коробках написано: “Два желтых”, “Два красных” и “Желтый и красный”. При этом известно, что ни одна из надписей не соответствует действительности. Из какой коробки, не глядя, надо вынуть шар, чтобы можно было определить содержимое каждой коробки?
Ответ: из коробки с надписью “Красный и желтый”.
(Учащимся можно предложить провести логические рассуждения при условии, если шар вынимается из любой другой коробки)
ПРИЛОЖЕНИЕ 5
Учитель:
Сегодня геометрия является одной из экологически чистых продуктов, потребляемых в образовании. Только геометрическое мышление пока сопротивляется “всеобщей компьютеризации”. Именно в области геометрии человек еще не проиграл интеллектуального соревнования компьютеру и поэтому развитие геометрического мышления является одной из важных задач школы.
7 класс. Найти величину угла между биссектрисами смежных и вертикальных углов.
Ответ: 90? и 180?.
9 класс. Отметьте 6 точек на плоскости так, чтобы на расстоянии ровно 1 см от каждой были ровно 3 другие.
Ответ: построить равносторонний треугольник со стороной 1 см и выполнить параллельный перенос на вектор 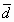 , где |
, где |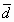 | = 1см, под углом 30? к основанию.
| = 1см, под углом 30? к основанию.
Общая задача
Представьте себе, что вы охватили земной шар по экватору. А теперь прибавьте к длине окружности 1 метр и снова охватите земной шар, у вас должен получиться зазор. Пролезет ли кошка через этот зазор?
(Такие нестандартные задачи у учащихся вызывают большой интерес. На первый взгляд, кажется, что ответ должен быть отрицательным, но если задачу перевести на язык геометрии, то нужно найти всего лишь разность между радиусами двух окружностей.)
В решении этой задачи принимают участие 2 группы. Вероятнее всего учащиеся 7 класса дадут отрицательный ответ, а учащиеся 9 класса будут производить математические выкладки.
Пусть С – длина окружности, тогда (С +1) – длина большей окружности. Радиус первой окружности равен 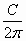 , радиус большей окружности равен
, радиус большей окружности равен 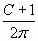 . Тогда величина зазора равна:
. Тогда величина зазора равна: 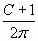 –
– 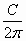 =
= 
ПРИЛОЖЕНИЕ 6
Вернемся к эмблеме занятия.
28k + 30n + 31m = 365
Слова учителя: Кто увидел? Кто догадался? Кто решил?
“Смотреть – не значит видеть!”
Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году. Тогда: 28 ·1 + 30 · 4 + 31 · 7 = 365.
ПРИЛОЖЕНИЕ 6:
Оцените свое отношение к занятию , закончив одну из фраз :
- сегодня мне понравилось …
- меня поразило …
- меня удивило …
- мне хотелось бы…
- я не в полнее удовлетворен тем, что …
Дополнительные задачи (если останется время).
Из 8 монет 1 монета фальшивая (более легкая). Как с помощью двух взвешиваний обнаружить ее на рычажных весах?
Денежная и весовая единица в Древнем Риме? (акр, талант, динар)















