Класс: 11 общеобразовательный.
| № этапа | Деятельность учителя | Деятельность учащихся |
| 1 урок: 1 | Учитель математики приветствует учащихся, предлагает учащимся задание на концентрацию внимания. Задание: Воспроизведите слова в указанном порядке (слова появляются на экране на несколько секунд, потом исчезают): Монотонность Асимптота Точность Единица Максимум Аргумент Точка Исследование Корень Абсцисса Рассчитайте концентрацию вашего внимания по формуле: число верно воспроизведённых слов *0,1*100% в указанном порядке Вывод: Это упражнение активизирует вашу зрительную память. А на данном уроке этот вид памяти необходим для лучшего усвоения нового материала. | Выполняют задание на концентрацию внимания (работа в тетрадях). |
| 2 | Предлагает учащимся выполнить задание в тетради: Построить графики показательных функций 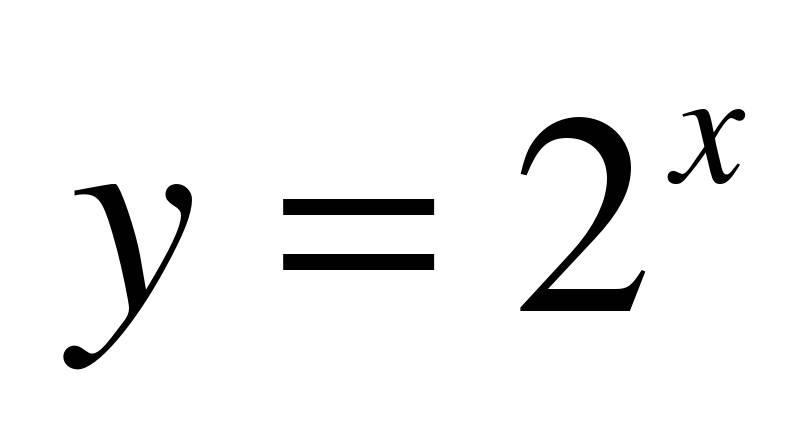 и и 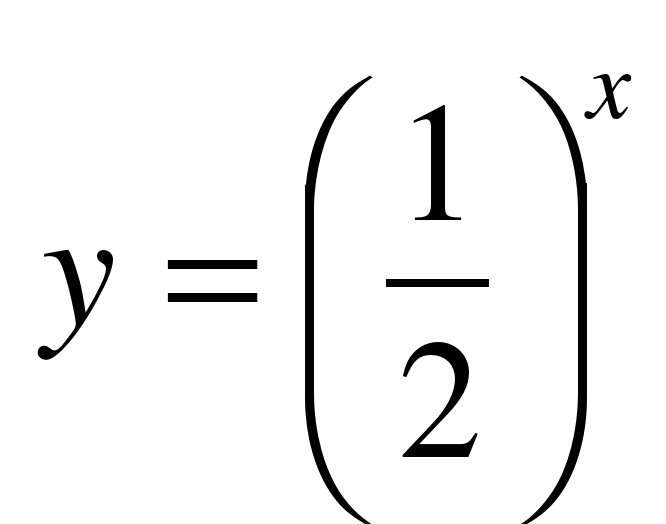 . . 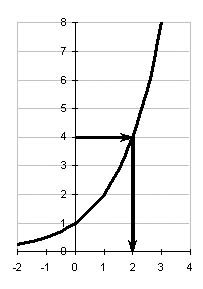 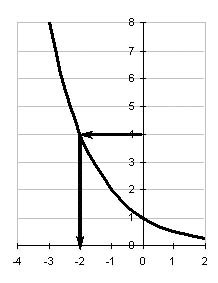
Предлагает учащимся сформулировать свойство монотонности функции 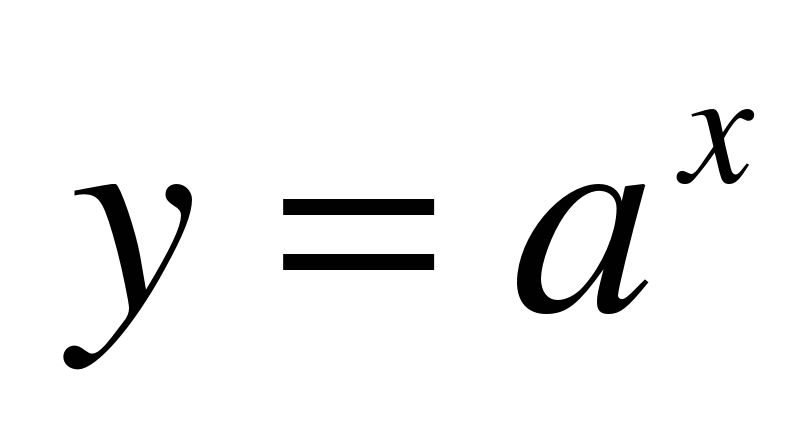 при а1, при 0 a при а1, при 0 a Формулировка: Функция y = ax (a 0, a 1) при a1 монотонно возрастает на R; при 0 a R. Для данной функции справедливо следующее утверждение: каждому значению y из области значений функции соответствует единственное значение x из области определения функции. | Выполняют построение графиков в тетради.
Устно формулируют свойство монотонности функции 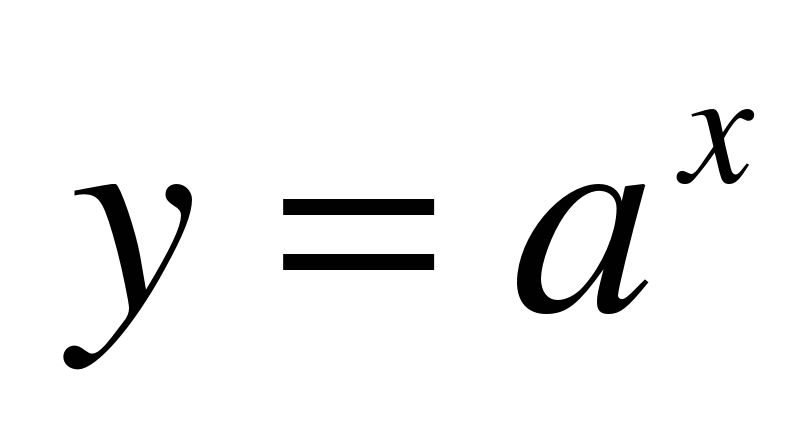 . . |
| 3 | Вводит понятие логарифмической функции. Пусть a положительное, не равное единице число. Каждому положительному числу x поставим в соответствие число y, равное логарифму числа x по основанию a, т. е. 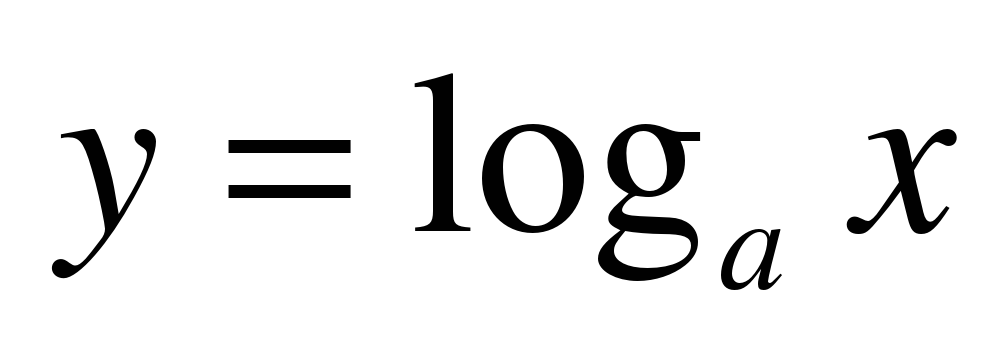 . . Определение: Функцию 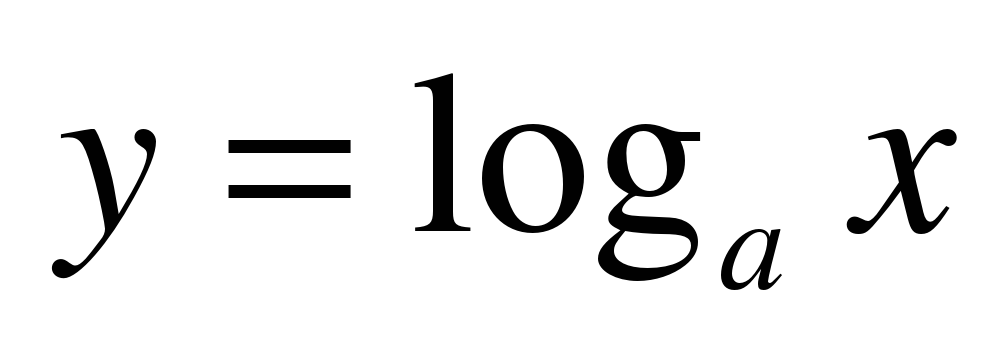 , (a 0, a 1) называют логарифмической функцией. , (a 0, a 1) называют логарифмической функцией. Предлагает учащимся сравнить области определения и области значений показательной и логарифмической функции. Результаты сравнения записать в таблицу: | g(x) = ax, a 0, a 1 | 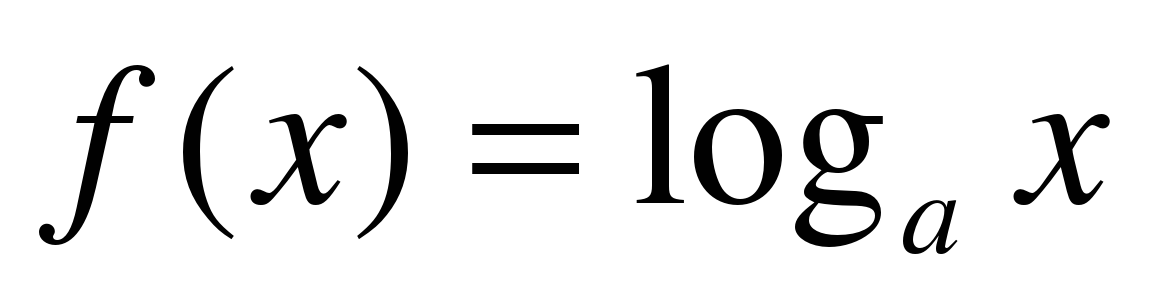 , a 0, a 1 , a 0, a 1
| | D(g) = R | D(f) = (0;+) | | E(g) =(0;+) | E(f) = R | По определению функции g(x) = ax, a 0, a 1 и f(x) = logax, a 0, a 1 являются взаимно обратными. Так как графики взаимно обратных функций симметричны относительно прямой h(x) = x, то 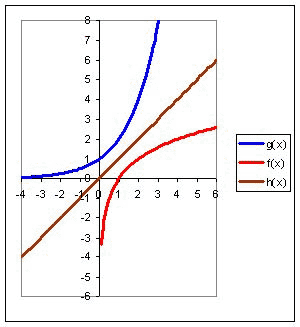 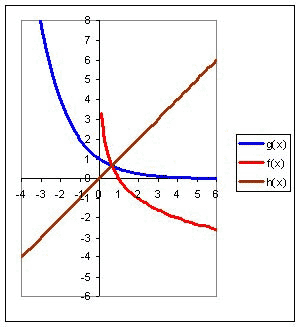 Предлагает построить в опорных конспектах графики логарифмических функций: y = log2x, y = log 1/2 x. | х | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | | у | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 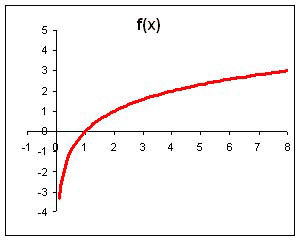 | х | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | | у | 3 | 2 | 1 | 0 | -1 | -2 | -3 | 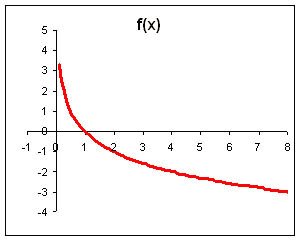
Свойства логарифмической функции |
| Свойства функции | а1 | 0 | | 1 | Область определения | (0;+) | | 2 | Область значений | (-;+) | | 3 | Четность, нечетность | ни четная, ни нечетная | | 4 | Нули функции | y = 0 при x = 1 | | 5 | Промежутки знакопостоянства | y 0 при x(1;+) y x (0;1) | y 0 при x (0;1) y x (1; +) | | 6 | Монотонность | возрастает | убывает | | 7 | Наибольшее и наименьшее значение функции | не существует | | 8 | Ограниченность | неограниченная | | 9 | Выпуклость | выпукла вверх | выпукла вниз |
| Слушают рассуждения учителя, записывают определение логарифмической функции в тетрадь.
Результаты сравнения записывают в таблицу, делают вывод о том, что показательная и логарифмическая функция является взаимно обратными.
Вспоминают алгоритм построения графиков в прямоугольной системе координат. Работают с опорными конспектами: заполняют таблицы значений (х, у), строят графики, записывают свойства логарифмической функции. |
| 4 | После изучения свойств логарифмической функции выполняются задания на применение этих свойств. Задание 1. Найти область определения функций: | y = logax, a 0, a 1 | D(y) | Решение | | y = log a(-x) | (-;0) | -х0 x | | y = log a(x)1/2 | (0;+ ) | x1/20 x0 | | y = log a(x-1) | (1;+ ) | x-10 x1 | | y = log a(x2-1) | (-;-1)(1;+ ) | x2-10 x x1 | | y = log a(x2+1) | R | x2+10 | | y = log a|x| | (-;0)(0;+ ) | | x|0 x|0 x0 x | Задание 2. Исследовать функцию на монотонность. Определить какие функции являются возрастающими, а какие убывающими: | y = log2x | возрастающая | 2 1 | | y = log0,5(2x + 5) | убывающая | 0 | | y = lg (x)1/2 | возрастающая | 10 1 | | y = ln(x + 2) | возрастающая | e 1 | Задание 3. Между числами m и n поставить знак или | log 0,5 m log 0,5 n | m n | 0 | | log 8 m log 8 n | m n | 8 1 | | log 2,5 m log 2,5 n | m n | 2,5 1 | | log 0,2 m log 0,2 n | m n | 0 | Предлагает учащимся выполнить задание из учебника «Алгебра и начала анализа» под ред. А. Г. Мордковича, М., Мнемозина, 2004. Номера для выполнения: №1467 (а, б) – нахождение наибольшего и наименьшего значения функции на заданном отрезке; № 1469 (а) – нахождение промежутка по указанному наибольшему и наименьшему значению функции; № 1492 (а) – нахождение области определения функции. Подводит промежуточный итог занятия: Мы познакомились с основными теоретическими выкладками темы «Логарифмическая функция и ее свойства». На следующем уроке мы продолжим отрабатывать навыки решения задач по данной теме, но уже с помощью компьютеров. Учитель информатики готовит класс к следующему уроку. | Работают в опорных конспектах, рассуждения по решению проводят устно, поочередно.
Работают в тетрадях, отдельные учащиеся выполняют задание на доске.
Выходят из класса на перемену. |
| 2 урок: 1 | Учитель информатики настраивает учащихся на рабочий лад, дает устную установку на продолжение учебной работы. | Учащиеся приветствуют учителя, занимают рабочие места. |
| 2 | Сообщает тему, цели и задачи урока. На уроках информатики мы изучаем прикладные программы, созданные для решения конкретных задач, например, обработку какого-либо вида информации. Давайте вспомним, изучали ли мы программу, которая позволяла бы обрабатывать числовую информацию, представлять ее в графическом виде. Это электронные таблицы Excel. Главное достоинство электронной таблицы – это возможность мгновенного пересчета всех данных, связанных формульными зависимостями при изменении значения любого операнда. Сегодня на уроке мы применим возможности табличного процессора Excel к решению конкретных задач курса математики, а именно задач на преобразование графиков логарифмической функции и решению систем уравнений. Таким образом, сегодня мы должны повторить навыки работы в Excel, убедиться в целесообразности изучения электронных таблиц, осознать, что знания, которые вы получаете на уроках информатики, можно применить, например, при подготовке к урокам математики. | Учащиеся приводят примеры изученных ими прикладных программ. Перечисляют возможности электронных таблиц Excel. |
| 3 | Предлагает учащимся обзор основных понятий, знание которых необходимо при работе в Excel. Электронная таблица Excel состоит из строк и столбцов. Строки нумеруются целыми числами, а столбцы – латинскими буквами A,B,C,…,AA,BB,… . На пересечении столбца и строки располагается структурный элемент таблицы – ячейка. В любую ячейку таблицы можно ввести исходные данные: число или текст, а также формулы для расчета производной информации. Для указания на конкретную ячейку используется адрес, который состоит из обозначения столбца и номера строки, на пересечении которых находится ячейка. Например А1, С4. Если набранная вами последовательность символов начинается со знака "=" (равно), Excel считает, что вы набрали формулу. В формулу могут входить данные разного типа, однако мы будем считать ее обычным арифметическим выражением, в которое можно записать только числа, адреса ячеек и функции, соединенные между собой знаками арифметических операций. Например, если вы ввели в ячейку D5 формулу «=А5*В5+C6», значением этой ячейки будет число, которое равно произведению чисел, записанных в А5 и В5, сложенному с числом из ячейки С6. Основным средством упрощения расчетов в Excel являются встроенные функции. Функция в Excel имеет имя (например, log) и, как правило, аргументы, которые записываются в круглых скобках следом за именем функции. Скобки – обязательная принадлежность функции, даже если у нее нет аргументов. Если аргументов несколько, они отделяются друга от друга запятой. Чтобы построить график функции на известном отрезке, необходимо, как и в математике, составить таблицу значений данной функции. С помощью автозаполнения сформировать строку значений х, для вычисления значения функции необходимо правильно составить формулу, описывающую эту функцию. Задание: Запишите функцию по правилам табличного процессора Excel: y = log3x Решение: =log(B2,3). Составим алгоритм построения графика функции. Выделить диапазон ячеек В2:L3 (таблицу значений) Выполнить команду Вставка/Диаграмма/Точечная/тип диаграммы «Гладкие графики» Определить параметры диаграммы: отобразить линии сетки (пунктиром), параллельные осям координат. Поместить график на имеющемся листе книги. 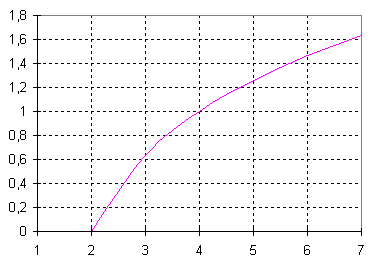 | В эвристической беседе вспоминают основные понятия Excel, составляют алгоритм построения графика функции в электронных таблицах. |
| 4 | Предлагает учащимся выполнить практические задания на компьютере. Задание 1: Постройте график функции: 1 вариант y = log3(x - 2) + 1 y = log1/3(x + 1) - 2 При участии учителя математики составляем алгоритм преобразования графиков вида y = log3(x + а) + b. 2 вариант y = log2(x + 1) – 2 y = log1/2(x - 3) + 1
| Садятся за компьютеры по двое. Выполняют задание по вариантам в электронных тетрадях. Записывают алгоритм преобразования графиков вида y = log3(x + а) + b в опорный конспект. Сохраняют свои работы в Документах, в папках со своими фамилиями. |
|
| Предлагает учащимся выполнить задание другого типа: решение систем уравнений графическим способом. С помощью графика функции можно определить количество корней уравнения и отрезки, внутри которых находятся эти корни. Задание 2: Решить графически систему уравнений: В ариант 1 ариант 1 y = log2x y = -x+1 на отрезке 0,5; 1,5 с шагом 0,1 Для этого необходимо составить таблицу значений для двух функций  Выделить диапазон ячеек В2:V3 и построить графики двух функций в одной координатной плоскости. Ответ: (1;0) 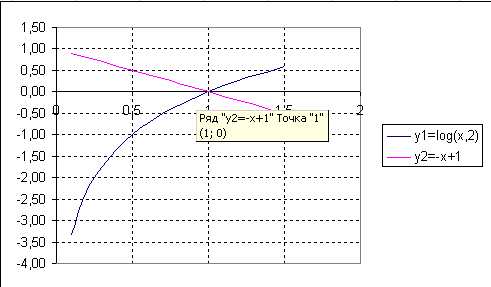  y = log1/3x y = 2x - 2 В ариант 2 ариант 2 y = log3x y = 4 – x 
y = log1/2x y = x + 1/2
| Выполняют задание по вариантам в электронных тетрадях. Сохраняют свои работы в Документах, в папках со своими фамилиями. |
| 5 | Предлагает учащимся записать домашнее задание, а выполнить его дома с помощью компьютера в среде электронных таблиц Excel. | Записывают домашнее задание |
| 6 | Подведение итогов двух уроков с помощью листков рефлексии, где указаны вопросы: Что я понял на уроке? Какой вид деятельности оказался для меня более успешным, результативным? Какие знания, умения приобрел? Какие знания, умения, навыки закрепил? Благодарит учащихся за работу на уроке | Заполняют листки рефлексии в опорных конспектах. |
Ф. И. О. конкурсантов: Исаенко Ольга Владимировна (учитель математики),
Калинина Олеся Витальевна (учитель информатики).
Организация, город: МОУ «СОШ № 55» г. Барнаула

















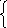 ариант 1
ариант 1




 0 , a 1. Каждому x0 поставим в соответствие число у, равное логарифму числа х по основанию а, т.е. y=log a х. Определение: Функцию y = log a x ( а 0, а 1 ) называют логарифмической функцией." width="640"
0 , a 1. Каждому x0 поставим в соответствие число у, равное логарифму числа х по основанию а, т.е. y=log a х. Определение: Функцию y = log a x ( а 0, а 1 ) называют логарифмической функцией." width="640"


 1 Область определения 2 0 Область значений 3 Четность, нечетность 4 Нули функции 5 Промежутки знакопостоянства 6 7 Монотонность Наибольшее и наименьшее значение функции 8 Ограниченность 9 Выпуклость" width="640"
1 Область определения 2 0 Область значений 3 Четность, нечетность 4 Нули функции 5 Промежутки знакопостоянства 6 7 Монотонность Наибольшее и наименьшее значение функции 8 Ограниченность 9 Выпуклость" width="640"



 или
или











