Тема урока: Логарифмы и их свойства
Цели урока: познакомиться с понятием логарифма; научиться находить логарифм по основанию а числа, представленного в виде степени с основанием а, записывать числа в виде логарифма с основанием а, применять основное логарифмическое тождество, а также логарифмировать выражения по указанному основанию.
Задачи урока:
Образовательные: повторить знания, полученные на предыдущих занятиях по теме «Показательная функция»; познакомить с понятием логарифма и научить их вычислять; установить связи преемственности в изучении нового материала с изученным, включить новые знания в систему ранее усвоенных; закрепить изученный на этом уроке материал .
Развивающие: развивать умственные и познавательные способности учащихся; развивать потребность в образовании, самообразовании, постоянном пополнении своих знаний, расширении общего кругозора; развивать творческое мышление.
Воспитательные: воспитание положительного отношения к знаниям, привитие интереса к изучаемому предмету, формирование навыков самоорганизации и самоконтроля, развитие познавательного интереса
Обучающийся должен знать: обозначение и определение логарифма числа, основное логарифмическое тождество.
Обучающийся должен уметь: находить логарифм числа, логарифмировать выражение, содержащее степень, применять основное логарифмическое тождество.
Тип урока: урок изучения нового учебного материала.
Форма проведения урока: фронтальная , индивидуальная, работа в парах.
Основные методы обучения: фронтальный, проблемный, частично-поисковый, наглядно-иллюстративный, информационно-коммуникационная технология.
Оборудование урока:
мультимедийный проектор
экран
компьютер - рабочее место учителя
презентация
раздаточный материал для учеников
Структура урока:
1.Организационный момент.
2.Мотивация учебной деятельности.
3. Актуализация опорных знаний.
4.Изучение нового материала.
5.Этап закрепления знаний.
6.Итоги урока.
7.Домашнее задание.
8.Рефлексия.
Ход урока.
1. Организационный момент (приветствие; проверка отсутствующих; проверка готовности к уроку)
2. Мотивация учебной деятельности.
Наш урок мне хотелось бы начать словами американского математика Мориса Клайна:
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
а математика способна достичь всех этих целей”.
Надеюсь эти слова станут хорошим стимулом для изучения новой темы и мотивируют вас на дальнейший интерес к изучению математики в целом.
Сегодня на уроке мы должны будем ответить на 5 ключевых вопросов, качающихся нашей темы: «ЧТО?», «КТО?», « КАК?», «ЗАЧЕМ?», «ГДЕ?».
3. Актуализация опорных знаний.
(Актуализация опорных знаний может быть основана на необходимости решения уравнения вида ax=b при условии, что правая часть не представима в виде степени)
Итак, давайте сформулируем цель, которая стоит перед нами на 1 этапе, отвечая на вопрос «ЧТО?» ( Узнать, что такое логарифмы.)
Начнем мы с устного решения показательных уравнений:
2x =4 2x =1 ( ½)x =8 2x =1/2 2x =5
(х = 2) ( х = 0) (х = -3) (х = -1) (х= ?)
Рассмотрим показательное уравнение 2x =5 .
Можем ли мы решить последнее уравнение? (Нет. Потому что правую и левую часть нельзя представить в виде степени по одному основанию.)
Проблема, которую предстоит решить, можно сформулировать следующим образом: «Как с достаточной степенью точности решить уравнение вида 2x=5?».
4. Изучение нового материала
(Эвристическая беседа с использованием наглядных материалов)
Решаем показательное уравнение 2x =5 .
Учащиеся ищут ответы на следующие вопросы:
- Что представляет собой левая часть уравнения?
- Что представляет собой правая часть уравнения?
- Какие способы решения уравнений известны?
- В чем заключается графический способ решения уравнения?
Применяя графический способ решения, по чертежу устанавливаем, что уравнение так же имеет единственное решение (по чертежу видим, что он заключен в промежутке от 2 до 3). Однако в отличие от предыдущих уравнений это решение является числом иррациональным (х = 2,321928…)
2 ≤ х ≤ 3,так как 22 3
Если корень показательного уравнения получается иррациональным, то как его лучше записать?
Для обозначения такого корня вводится новое понятие и новый символ – логарифм.
Корень уравнения 2x =5, x = log25.
Очень часто приходится решать подобную задачу: известно, что ax=b. Необходимо найти показатель степени х, то есть решать задачу, обратную возведению числа в степень. При нахождении этого показателя степени х и возникает понятие логарифма числа b по основанию а.
Обозначается x = logab. Даем определение логарифма.
(Предлагается обучающимся прочитать определение логарифма вслух и про себя. )
Определение:
Логарифмом положительного числа b по положительному и не равному единице основанию a называется показатель степени, в который надо возвести число a, чтобы получить b.
x = logab a x = b
(где a0, a≠1, b0)
Операцию нахождения логарифма числа называют логарифмированием.
(Операция логарифмирования является обратной для операции возведения в степень с соответствующим основанием. На слайде № 12 презентации рассматриваются примеры взаимно обратных действий)
Из определения логарифма следует равенство:
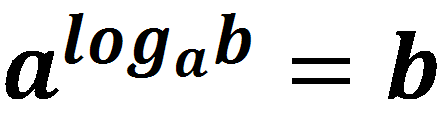
Это равенство называется основным логарифмическим тождеством.
Равенство справедливо при b 0, a 0, a ≠ 1.
Рассмотрим примеры применения основного логарифмического тождества:
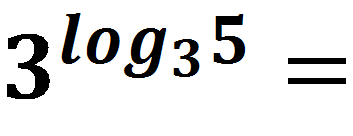
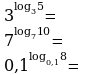 5
5 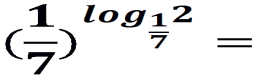 2
2
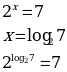
Из определения логарифма следует ещё три важные формулы

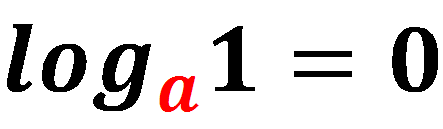
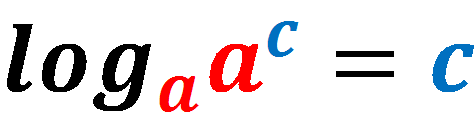 .
.
Мы познакомились с новым для вас понятием логарифма. Теперь перейдем к следующему ключевому вопросу «КТО?».
Сформулируйте цель следующего этапа урока, отвечая на второй вопрос «КТО?» (Выяснить, кто впервые ввёл понятие логарифма.)
Откройте стр. 269-270 учебника и прочитайте историческую справку.
КТО автор изобретения логарифмов? (Джон Непер)
ИСТОРИЧЕСКАЯ СПРАВКА
Логарифмы были придуманы для ускорения и упрощения вычислений. Идея логарифма, т. е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю.
Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития.
Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским учёным Джоном Непером (1550-1617) и швейцарцем Иобстом Бюрги (1552-1632).
Слово «логарифм» происходит от греческих слов logoz и ariumoz - оно означает буквально “числа отношений”.
Впервые понятие логарифма ввел английский математик Джон Непер, о чем сообщалось в публикации 1614 года, когда была опубликована работа Непера под названием «Описание удивительной таблицы логарифмов».
Кроме того, этот человек известен тем, что он первый изобрел таблицу логарифмов, которая пользовалась большой популярностью среди ученых на протяжении долгих лет. Первые таблицы десятичных логарифмов были составлены в 1617 г. английским математиком Бриггсом.
Изобретатели логарифмов не ограничились созданием логарифмических таблиц, уже через 9 лет после их разработки в 1623 г. английским математиком Гантером была создана первая логарифмическая линейка. Она стала рабочим инструментом для многих поколений инженеров (до 70-х годов нашего века). В настоящее время мы можем находить значения логарифмов, используя компьютер. Так, в языке программирования BASIC с помощью встроенной функции можно находить натуральные логарифмы чисел.
5. Этап закрепления знаний.(Решение задач с целью усвоения понятия логарифма)
Переходим к следующему вопросу «КАК?». Сформулируйте цель этого этапа урока. (Узнать как вычисляются логарифмы. Научиться вычислять логарифмы)
Р ассмотрим примеры вычисления логарифмов:
ассмотрим примеры вычисления логарифмов:
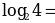
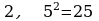
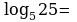
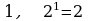
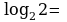
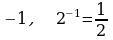

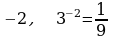
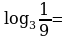
Р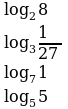
 ешите устно тренировочные упражнения:
ешите устно тренировочные упражнения:
Выполняем № 758 в тетрадях. Работаем вместе с доской. (К доске выходит один учащийся и решает примеры 1, 2 и 3).
Разберем следующие примеры на вычисления:
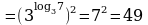

Какие свойства степени и новые полученные знания мы здесь можем применить? (степень степени, основное логарифмическое тожество, определение степени)

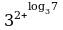
Какие свойства степени и новые полученные знания мы здесь можем применить? ( сумма степеней, основное логарифмическое тожество, определение степени.)
Работа в парах.
Разобраться как решить уравнение № 764.
1 пара – 1 и 2,
2 пара - 3 и 4,
3 пара – 5 и 6.
К доске по одному от каждой пары решить по одному уравнению.
На очереди следующий вопрос «ЗАЧЕМ?». Сформулируем цель данного этапа урока, отвечая на поставленный вопрос. (Выяснить зачем изучают логарифмы).
«Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней словно удваивает жизнь астрономов»
П.С. Лаплас
Откройте учебник и прочитайте информацию на странице 241.
Логарифмы упрощают вычисления, позволяют решать показательные уравнения, где правая часть не может быть выражена в виде степени, находить показатель степени, т.е. выполнять операцию, обратную возведению в степень. Логарифмы широко используются при решении различных теоретических и практических задач.
ЦЕННОСТЬ ЛОГАРИФМОВ
состоит в сведении сложных действий возведения в степень и извлечения корня к более простым действиям - умножению и делению, а последних к - самым простым – сложению и вычитанию.
Поэтому открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию их логарифмов упростило жизнь тех, кто по роду своей деятельности был связан с громоздкими вычислениями и сложными расчетами.
Как не правы те друзья,
что утверждают смело:
логарифмы – ерунда,
не нужны для дела.
Логарифмы – это всё:
музыка и звуки,
и без них никак нельзя
обойтись в науке!
Вот мы перешли к последнему вопросу «ГДЕ?». Сформулируйте цель. Что мы должны узнать отвечая на этот вопрос? (Узнать, где применяются логарифмы.)
Логарифмы широко используются в различных областях науки, например:
Физика— интенсивность звука (децибелы).
Астрономия — шкала яркости звёзд.
Химия — активность водородных ионов.
Сейсмология — шкала Рихтера.
Теория музыки — нотная шкала, по отношению к частотам нотных звуков.
История — логарифмическая шкала времени.
ОКАЗЫВАЕТСЯ…
Математическим символом соотношения формы и роста является
логарифмическая спираль. Эта спираль пересекает все прямые, проходящие через полюс под одним и тем же углом.
Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее аналогиям. Поэтому раковины многих моллюсков, улиток, закручены по логарифмической спирали.
Рога таких животных, как архары, закручены по логарифмической спирали. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.
По логарифмической спирали формируется и тело циклона, закручены и многие галактики, в частности – Галактика Солнечной системы.
6. Итоги урока. Вот мы ответили на все поставленные в начале урока вопросы.
О сновные результаты урока :
сновные результаты урока :
Ввели обозначение для записи корня уравнения вида
П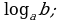 ополнили словарный запас математического языка понятиями логарифм числа, основание логарифма;
ополнили словарный запас математического языка понятиями логарифм числа, основание логарифма;
7. Домашнее задание: учебник «Алгебра и начала математического анализа. 10 класс» под редакцией Ю.М. Колягина. Глава 7, § 1, №756, 757, 759, 762
8. Рефлексия
Ответьте на вопросы и самостоятельно оцените свою работу на уроке по 10 бальной шкале.
- Как ты считаешь, полезным ли было проведенное занятие?
- Получены ли новые знания и умения?
- Какие моменты занятия особенно запомнились?
- Каких моментов занятия хотелось бы избежать?
Оцени свою работу на уроке по 10 бальной шкале (поставь свою точку на шкале).






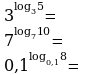 5
5 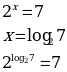
 ассмотрим примеры вычисления логарифмов:
ассмотрим примеры вычисления логарифмов: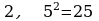
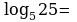
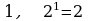
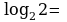
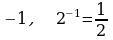

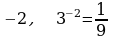
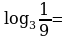
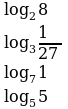
 ешите устно тренировочные упражнения:
ешите устно тренировочные упражнения: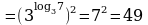


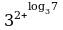
 сновные результаты урока :
сновные результаты урока :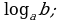 ополнили словарный запас математического языка понятиями логарифм числа, основание логарифма;
ополнили словарный запас математического языка понятиями логарифм числа, основание логарифма;