СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Разработка методического кейса по теме « Степенная функция, её свойства и график» по предмету «Алгебра и начала математического анализа в 10 классе
Актуальность темы «Степенная функция» обусловлена сложившимися к настоящему времени противоречиями между: необходимостью качественного усвоения обучающимися понятия функции в углубленном курсе математики общеобразовательной школы и недостаточной разработанностью методики его формирования
Просмотр содержимого документа
«Разработка методического кейса по теме « Степенная функция, её свойства и график» по предмету «Алгебра и начала математического анализа в 10 классе»
ВВЕДЕНИЕ
В связи с внедрением новых Государственных образовательных стандартов углубляется перестройка школы, целью которой является обеспечение высокого качества образования и развития учащихся. В связи с этим внимание ученых-математиков, педагогов, психологов сосредоточено на поиске эффективных средств изучения предмета математики. Специфика математики как предмета состоит в том, что: 1) понятия математики представляют собой сложную логико-гносеологическую категорию высокого уровня абстракции по сравнению с предметами естественнонаучного цикла; 2) процесс образования, развития и применения математических понятий – сложный, длительный, многоуровневый и многоэтапный процесс.[13]
В целях повышения теоретического уровня, мировоззренческой и практической направленности предметного обучения программы и учебники по математике неоднократно совершенствовались. Произошли заметные позитивные изменения в понятийном аппарате школьного курса математики: уточнены и усилены многие теоретические знания, модельные представления.
Как известно, «эффективность обучения математике во многом определяется системой работы учителя, одним из важных компонентов которой является методика формирования основных математических понятий».[8] К числу основных понятий современной математики относится понятие функции, которое прошло долгий исторический путь развития, прежде чем вошло в науку и школьный курс математики. Функциональная линия - один из основных разделов содержательных линий школьного курса алгебры. Она пронизывает целый курс математики. В 5–6-х классах осуществляется функциональная пропедевтика, в 7-9 классах происходит систематическое изучение функционального материала. Затем тема «Функции» продолжает изучаться в старших классах.
Ю.М. Колягин в учебном пособии «Методика преподавания математики в средней школы: Частные методики» утверждает, что «понятие функции – одно из фундаментальных математических понятий, непосредственно связанных с реальной действительностью. В нем ярко воплощены изменчивость и динамичность реального мира, взаимная обусловленность реальных объектов и явлений. Функции, их свойства и графики образуют основу школьного курса математики. Вокруг функциональной линии группируется вся современная школьная алгебра, начала математического анализа и в некоторой степени геометрия. Специфичность данной линии заключается в ее возможности устанавливать в обучении внутрипредметные и межпредметные связи» .[9]
Немецкий математик и педагог Ф. Клейн (1849 – 1925) был убежден в ведущей роли понятия функции и в математике-науке, и в обучении математике. Ф. Клейн в книге «Элементарная математика с точки зрения высшей» писал: «Какое же понятие в современной математике доминирует? Это есть понятие о функции. Понятие о функции должно играть основную, так сказать, руководящую роль в курсе средней школы. Понятие это должно быть выяснено учащимися очень рано и должно пронизывать все преподавание алгебры и геометрии». [10]
Согласно государственному образовательному стандарту среднего общего образования результаты изучения предметной области «Математика» должны отражать: 1) сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
2) сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей. [3]
Таким образом, актуальность темы «Степенная функция» обусловлена сложившимися к настоящему времени противоречиями между: необходимостью качественного усвоения обучающимися понятия функции в углубленном курсе математики общеобразовательной школы и недостаточной разработанностью методики его формирования. [10]
Объект исследования – это процесс изучения учащимися алгебры и начал математического анализа.
Предметом исследования является изучение свойств степенной функции в школьном курсе алгебры.
Цель работы - разработка цикла уроков по предмету «Алгебра и начала математического анализа» для 10 класса по теме: «Степенная функция».
Для достижения цели необходимо решить следующие задачи:
изучить структуру современного урока и проблему методического обеспечения уроков предмета «Алгебра и начала математического анализа» в педагогической и методической литературе;
проанализировать требования учебной программы к уровню знаний и умений учащихся 10 классов по теме: «Степенная функция»;
разработать цикл уроков для 10 класса по теме: «Степенная функция».
Для достижения целей работы и решения поставленных выше задач были использованы следующие методы:
а) анализ программы по алгебре и началам математического анализа, учебных пособий, методических материалов, касающихся степенной функции;
б) изучение и обобщение опыта преподавания темы «Степенная функция»;
в) наблюдение за ходом образовательного процесса, за деятельностью учащихся.
Практическая значимость данной работы состоит в том, что разработанная система изучения темы методически доведена до возможности непосредственного использования учителями на уроках. Она позволит учителю всесторонне подготовиться к занятию, а также показать при этом высокие результаты во владении теоретическим материалом и решении практических задач, повысит общий уровень знаний по предмету.
Структура работы: работа состоит из введения, двух разделов, выводов, списка использованных источников, приложения.
РАЗДЕЛ 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ СТЕПЕННОЙ ФУНКЦИИ
1.1. Из истории возникновения функции
На протяжении всего школьного курса мы сталкиваемся с функциями и графиками. До 10 класса – это простые функции, в 10-11 классах изучаются сложные функции, однако, им уделяется не так уж много внимания. Особенно это касается методов построения графиков таких функций. А ведь это, пожалуй, один из самых интересных вопросов в курсе алгебры. Более того, графики сложных функций чаще всего получаются очень красивыми и необычными, поэтому изучение этого материала приносит не только практическую пользу, но и в какой-то мере эстетическое удовлетворение.
Понятие функции уходит своими корнями в ту далёкую эпоху, когда люди впервые поняли, что окружающие их предметы взаимосвязаны. [11]
Когда возникли первые цивилизации, образовались большие армии, началось строительство гигантских пирамид, древние учёные стали составлять таблицы для облегчения вычислений. В Древнем Вавилоне были составлены таблицы для функций y =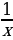 , y=x2, y= x3, y= x2+x3. Понятие переменной величины было введено в науку французским учёным и математиком Рене Декартом (1596-1650). Он ввёл идею числовой функции числового аргумента. При записи зависимостей между величинами Декарт стал применять буквы. Он начал геометрически изображать не только пары чисел, но и уравнения, связывающие два числа. [11]
, y=x2, y= x3, y= x2+x3. Понятие переменной величины было введено в науку французским учёным и математиком Рене Декартом (1596-1650). Он ввёл идею числовой функции числового аргумента. При записи зависимостей между величинами Декарт стал применять буквы. Он начал геометрически изображать не только пары чисел, но и уравнения, связывающие два числа. [11]
Одновременно с Декартом к мысли о соответствии между линиями и уравнениями пришёл другой французский математик – Пьер Ферма (1601-1665). Он был советником тулузского парламента и занимался математическими исследованиями лишь в свободное время. Тем не менее, Ферма получил ряд первоклассных результатов в различных областях математики.
Термин «функция» начал применять в конце XVII века Лейбниц (1646-1716) и его ученики. [11]
Определение функции, приближенное к современному, дал Иоганн Бернулли: «Функцией переменной величины называется количество, образованное каким угодно способом из этой переменной величины и постоянных».
Современное определение функции разительно отличается от определения, данного Бернулли. Функция, или функциональная зависимость – это такая зависимость между двумя переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной. Независимую переменную иначе называют аргументом, а о зависимой говорят, что она является значением функции. [11]
В математике есть 4 способа задания функции:
1. С помощью таблицы.
2. Графический.
3. С помощью формулы.
4. Описательный.
Подробнее всего функцию описывает график. Графиком функции называют множество точек координатной плоскости абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. Область определения – это все значения, которые может принимать независимая переменная (аргумент функции). Кроме области определения существует ещё и множество значений – это все значения, которые может принимать зависимая переменная. Эти свойства функции являются важнейшими, но есть и другие немаловажные свойства: промежутки знакопостоянства, монотонность, нули функции, разрывность, периодичность, ограниченность, чётность/нечётность. С помощью графика можно исследовать практически все свойства функции.
1.2. Степенная функция, ее свойства и график
Особый интерес в математике вызывает «Степенная функция». На изучение темы «Степенная функция» отводится 18 часов:
| № | Тема урока | К-во часов |
| Свойства степенной функции. Уравнения и неравенства (9 часов) | ||
| 1-2 | Степенная функция, ее свойства и график | 2 |
| 3-4 | Взаимно обратные функции | 2 |
| 5-6 | Равносильные уравнения и неравенства | 2 |
| 7 | Решение задач | 1 |
| 8 | Контрольная работа | 1 |
| 9 | Анализ контрольной работы | 1 |
| Уравнения и неравенства со знаком модуля (9 часов) | ||
| 1 | Уравнения со знаком модуля | 1 |
| 2 | Неравенства со знаком модуля | 1 |
| 3 | Иррациональные уравнения | 1 |
| 4 | Иррациональные неравенства | 1 |
| 5 | Параметр в уравнении с модулем | 1 |
| 6 | Параметр в иррациональном уравнении | 1 |
| 7 | Решение задач | 1 |
| 8 | Контрольная работа | 1 |
| 9 | Анализ контрольной работы | 1 |
Данная тема изучается в начале 10 класса и является основой для изучения показательной и логарифмической функций. В основной школе обучающиеся знакомы с темой «Степень с натуральным показателем» (7 класс), «Степень с целым показателем» (8 класс), изучены свойства степени, обучающиеся умеют преобразовывать выражения, содержащие степень. Также, на уровне основной школы обучающиеся познакомились с такими понятиями как функция, область определения и область значений функции, свойствами функции.
В 10 классе процесс изучения тем «Степень» и «Функция» расширился. Обучающимся предложено углубить полученные знания и познакомиться, что же собой представляет степенная функция в зависимости от показателя р.
Содержание курса по теме «Степенная функция».
Степенная функция, ее свойства и график. Взаимно обратные функции. Равносильные уравнения и неравенства. Уравнения со знаком модуля. Неравенства со знаком модуля. Иррациональные уравнения. Иррациональные неравенства. Параметр в уравнении с модулем. Параметр в иррациональном уравнении.
Основная цель:
обобщить и систематизировать известные из курса алгебры основной школы свойства функций;
изучить свойства степенных функций с натуральным и целым показателями и научить применять их при решении уравнений и неравенств;
сформировать понятие равносильности уравнений, неравенств, систем уравнений и неравенств.
Рассмотрение свойств степенных функций и их графиков проводится поэтапно, в зависимости от того, каким числом является показатель:
1) четным натуральным числом;
2) нечетным натуральным числом;
3) числом, противоположным четному числу;
4) числом, противоположным нечетному числу; 5) положительным нецелым числом;
6) отрицательным нецелым числом.
Обоснования свойств степенной функции не проводятся, они следуют из свойств степени с действительным показателем.
Например, возрастание функции у = хр на промежутке х 0, где р — положительное нецелое число, следует из свойства: «Если 0 1 2, р 0, то х1р 2р». На примере степенных функций учащиеся знакомятся с понятием ограниченной функции, учатся доказывать, как ограниченность, так и неограниченность функции. Рассматриваются функции, называемые взаимно обратными. Важно обратить внимание на то, что не всякая функция имеет обратную. Доказывается симметрия графиков взаимно обратных функции относительно прямой у = х. Обращается внимание учащихся на отыскание области определения сложной функции и промежутков ее монотонности. Доказывается теорема о промежутках монотонности с опорой на определения возрастающей или убывающей функции, что позволяет изложить суть алгоритма доказательства монотонности сложной функции. Учащиеся знакомятся с дробно-линейными функциями. В основной школе учащиеся учились строить график функции у = 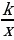 и графики функций, которые получались сдвигом этого графика. Выделение целой части из дробно-линейного выражения приводит к знакомому учащимся виду функции. Умение применять определение модуля при решении уравнений и неравенств, содержащих знак модуля. Использование схем равносильных переходов. Рассмотрение равносильности уравнений, неравенств и систем уравнений и свойств равносильности проводится в связи с предстоящим изучением иррациональных уравнений и неравенств. Основным методом решения иррациональных уравнений является возведение обеих частей уравнения в степень с целью перехода к рациональному уравнению-следствию данного. При решении уравнений с параметром следует обратить внимание, что при записи ответа следует рассматривать все допустимые значения параметра. С помощью графиков решается вопрос о наличии корней и их числе, а также о нахождении приближенных корней, если аналитически решить уравнение трудно. Иррациональные неравенства не являются обязательными для изучения всеми учащимися. При их изучении основным способом решения является сведение неравенства к системе рациональных неравенств, равносильной данному неравенству. [5]
и графики функций, которые получались сдвигом этого графика. Выделение целой части из дробно-линейного выражения приводит к знакомому учащимся виду функции. Умение применять определение модуля при решении уравнений и неравенств, содержащих знак модуля. Использование схем равносильных переходов. Рассмотрение равносильности уравнений, неравенств и систем уравнений и свойств равносильности проводится в связи с предстоящим изучением иррациональных уравнений и неравенств. Основным методом решения иррациональных уравнений является возведение обеих частей уравнения в степень с целью перехода к рациональному уравнению-следствию данного. При решении уравнений с параметром следует обратить внимание, что при записи ответа следует рассматривать все допустимые значения параметра. С помощью графиков решается вопрос о наличии корней и их числе, а также о нахождении приближенных корней, если аналитически решить уравнение трудно. Иррациональные неравенства не являются обязательными для изучения всеми учащимися. При их изучении основным способом решения является сведение неравенства к системе рациональных неравенств, равносильной данному неравенству. [5]
Основные понятия в теме «Степенная функция».
Функция вида у = хр, где р – заданное действительное число, называется степенной функцией. [6]
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень хр.
Обычно указывают следующие свойства:
1.Область определения - все значения которые принимает аргумент х.
2.Область значений (множество значений) - все значения, которые принимает функция у.
3.Четность, нечетность функции. Графическая иллюстрация четной, нечетной функции: симметрия относительно Ох, Оу. Аналитическая запись свойства четности, нечетности: х ϵ R, f(x)= f(-x); f(x)=- f(x).
4.Промежутки возрастания и убывания функции: большему значению аргумента соответствует большее (меньшее) значение функции.
5.Промежутки знакопостоянства: у 0, y
Новыми для изучения в 10-11 классах являются следующие определения.
Определение 1. Функция у = f(х), определенная на множестве Х, называется ограниченной снизу на множестве Х, если существует число а такое, что для любого х ϵ Х выполняется неравенство f(х) ≥ а. [6]
| Пример: | |
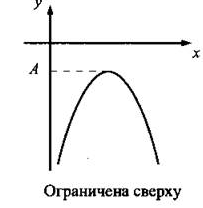
Определение 2. Функция у = f(х), определенная на множестве Х, называется ограниченной сверху на множестве Х, если существует число А такое, что для любого х ϵ Х выполняется неравенство f(х) ≤ А. [6]
| Пример: | |
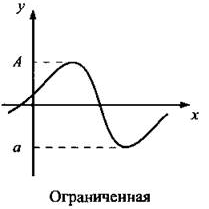
Определение 3. Функцию, ограниченную и сверху, и снизу на множестве Х, называют ограниченной на этом множестве. [6]
| Пример: | |
1.3.Различные случаи графиков степенной функции у = хр в зависимости от показателя степени р
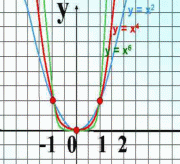
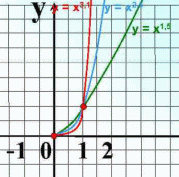
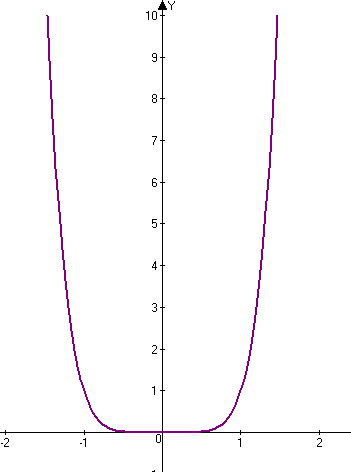
| Показатель р = 2n – четное натуральное число. Например: у = х2, у = х4, у = х6, у = х8, ….. | |
|
| Свойства: 1)D(у): хꞓR. 2)Е(у): у≥0. 3)Функция четная, т.к. (-х)2n = x2n. 4)Убывает, если х≤0, возрастает, если х≥0. 5)Функция ограничена снизу. 6)Наименьшее значение у = 0 при х = 0. Наибольшего значения нет. |
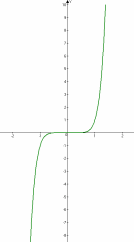
| 2.Показатель р = 2n - 1 – нечетное натуральное число. Например: у = х3, у = х5, у = х7, у = х9, ….. | |
| | Свойства: 1)D(у): хꞓR. 2)Е(у): уꞓR. 3)Функция нечетная, т.к. (-х)2n-1 = - x2n-1. 4)Возрастает на всей области определения. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет. |
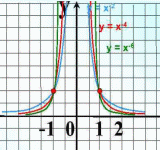
| 3.Показатель р = - 2n – где n - натуральное число. Например: у = х-2 = | |
|
| Свойства: 1)D(у): х≠0. 2)Е(у): у0. 3)Функция четная, т.к. 4)Возрастает при х 0. 5)Функция ограниченна снизу. 6)Наибольшего и наименьшего значения нет. |
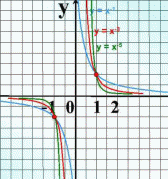
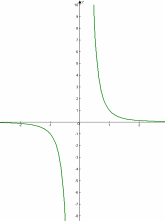
| 4. Показатель р = -(2n – 1) – где n - натуральное число. Например: у = х-1 = | |
|
| Свойства: 1)D(у): х≠0. 2)Е(у): у≠0. 3)Функция нечетная, т.к. 4) Убывает при х 0. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет. |
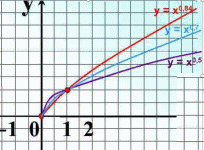
| 5. Показатель р – положительное действительное нецелое число. Например: у = | |
|
| Свойства: 1)D(у): х≥0. 2)Е(у): у≥0. 3)Функция ни четная, ни нечетная. 4)Возрастает, если х≥0. 5)Функция ограничена снизу. 6)Наименьшее значение у = 0 при х = 0. Наибольшего значения нет. |
| Примеры показательной функции, где р – положительное действительное нецелое число. | |
|
| |
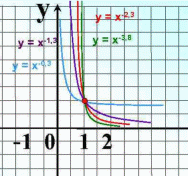
| 6. Показатель р – отрицательное действительное нецелое число. Например: у = | |
|
| Свойства: 1)D(у): х0. 2)Е(у): у0. 3)Функция ни четная, ни нечетная. 4)Убывает, если х0. 5)Функция ограничена снизу. 6)Наименьшего и наибольшего значения нет. |
1.4. Взаимно обратные функции
Итак, что же такое функция?
Определение: Если каждому значению х из множества действительных чисел ставится в соответствие по определенному правилу единственное значение у, то говорят, что на этом множестве определена функция у = f(х). [6]
Определение: Если функция у = f(х) принимает каждое свое значение только при одном значении х, то эту функцию называют обратимой.
Пусть у = f(х) – обратимая функция. Тогда каждому у из множества значений функции соответствует одно определенное число х из области ее определения, такое, что f(x) = у. Это соответствие определяет функцию х от у, которую обозначим х = g(у). Поменяем теперь местами х и у, получим у = g(х). [6]
Функцию у = g(х) называют обратной к функции у = f(х).
Область определения обратной функции совпадает с множеством значений исходной функции, а множество значений обратной функции совпадает с область определения исходной функции.
Возрастающие и убывающие функции называют одним словом – монотонные. [6]
Если функция у = f(х) возрастает, то обратная к ней функция g(х) также возрастает; если функция у = f(х) убывает, то обратная к ней функция g(х) также убывает. [6]
АЛГОРИТМ НАХОЖДЕНИЯ ФУНКЦИИ, ОБРАТНОЙ ДАННОЙ
Определить, будет ли функция обратимой?
Выразить переменную х через переменную у.
Поменять местами х и у.
Теорема 1. Монотонная функция является обратимой.
Доказательство:
Пусть функция у = f(х) возрастает и пусть у0 – ее значение в некоторой точке х0, т.е. у0 = f(х0). Тогда если х принадлежит области определения функции, то при х х0 выполняется неравенство f(x) f(x0) = y0, а при х 0 – неравенство f(x) f(x0) = y0. Следовательно, значение у0 функция f(x) принимает только в одной точке х0 и поэтому является обратимой. Теорема доказана. [6]
Теорема 2. Если функция имеет обратную, то график обратной функции симметричен графику данной функции относительно прямой у = х.
Доказательство:
Если точка (х0; у0) принадлежит графику функции у = f(x), то точка (у0; х0) принадлежит графику обратной функции у = g(х), см. рисунок:
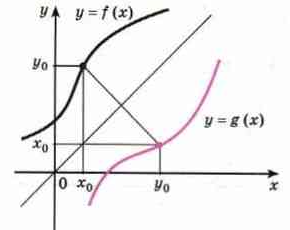
Точки (х0; у0) и (у0; х0) симметричны относительно прямой у = х, см. рисунок:
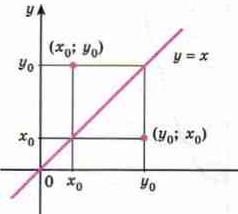
Теорема доказана. [6]
1.5. Равносильные уравнения и неравенства
Определение 1. Уравнения, имеющие одно и то же множество корней, называются равносильными. [6]
Уравнения, не имеющие корней, также являются равносильными.
Из определения равносильности следует, что два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого уравнения.
Какие преобразования можно осуществлять при решении уравнений?
Любой член уравнения можно переносить из одной части в другую, изменив его знак на противоположный.
Обе части уравнения можно умножить или разделить на одно и то же число, отличное от нуля.
Определение 2. Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют следствием первого уравнения. [6]
Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Значит:
1)Если два уравнения равносильны, то каждое из них является следствием другого.
2) Если каждое уравнение является следствием другого, то эти уравнения равносильны.
Посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное.
Потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.
Определение 3. Неравенства с неизвестной, имеющие одно и то же множество решений, называются равносильными. [6]
Неравенства, не имеющие решений, также являются равносильными.
Из определения равносильности следует, что два неравенства равносильны, если множество решений первого неравенства совпадает с множеством решений второго неравенства и, наоборот, множество решений второго неравенства является множеством решений первого неравенства.
РАЗДЕЛ 2. «РАЗРАБОТКА МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ ПРЕПОДАВАНИЯ ТЕМЫ «СТЕПЕННАЯ ФУНКЦИЯ» ПРЕДМЕТА «АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА» В 10 КЛАССЕ
Целью данной выпускной работы является подготовка учебно-методических материалов по алгебре и началам математического анализа для 10-х классов, необходимых для реализации основной образовательной программы среднего общего образования предмета «Алгебра и начала математического анализа» в 10 классе.
В данной работе разработан комплекс, включающий в себя, конспекты уроков, электронные презентации и задания для самостоятельных и контрольных работ для каждого урока алгебра в 10 классе по теме: «Степенная функция».
Данная разработка составлена в соответствии с Примерной основной образовательной программой по учебному предмету «Алгебра и начала математического анализа». 10-11 классы (базовый, углубленный уровни) / сост. Скафа Е.И., Федченко Л.Я., Полищук И.В. – 5-е изд. перераб., дополн. – ГОУ ДПО «ДонРИДПО». – Донецк: Истоки, 2020. – 52 с. и полностью соответствует календарно-тематическому планированию курса «Алгебра и начала математического анализа» (углубленный компонент) [5].
Представленные методические разработки – это пособие, которое практически и теоретически раскрывает применяемую программу, методы и средства обучения, современные технологии в соответствии с темой и возрастными психолого-физиологическими особенностями учащихся. Разработки соответствуют выбранной теме «Степенная функция» и в полной мере раскрывают поставленные цели уроков. Работы имеют новизну, являются актуальными. В методических разработках использованы эффективные способы обучения, методические приемы, которые способствуют достижению целей уроков. Реализация материала производится с помощью электронных презентаций и раздаточного материала.
Планируемые результаты освоения учащимися учебного материала по теме «Степенная функция».
Учащийся научится:
Владеть понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, уметь применять эти понятия при решении задач;
владеть понятием степенная функция; строить ее график и уметь применять свойства степенной функции при решении задач;
владеть понятием обратная функция; применять это понятие при решении задач;
применять при решении задач свойства функций: четность, периодичность, ограниченность;
применять при решении задач преобразования графиков функций;
Свободно оперировать понятиями: уравнение, неравенство, равносильные уравнения и неравенства, уравнение, являющееся следствием другого уравнения, уравнения, равносильные на множестве, равносильные преобразования уравнений;
понимать смысл теорем о равносильных и неравносильных преобразованиях уравнений и уметь их доказывать;
владеть методами решения уравнений, неравенств и их систем, уметь выбирать метод решения и обосновывать свой выбор;
использовать метод интервалов для решения неравенств, в том числе дробно-рациональных.
В повседневной жизни и при изучении других учебных предметов:
определять по графикам и использовать для решения прикладных задач свойства реальных процессов и зависимостей (наибольшие и наименьшие значения, промежутки возрастания и убывания функции, промежутки знакопостоянства, асимптоты, точки перегиба, период и т.п.);
интерпретировать свойства в контексте конкретной практической ситуации;
определять по графикам простейшие характеристики периодических процессов в биологии, экономике, музыке, радиосвязи и др. (амплитуда, период и т.п.);
выполнять оценку правдоподобия результатов, получаемых при решении различных уравнений, неравенств при решении задач других учебных предметов.
Учащийся получит возможность:
Оперировать понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, четная и нечетная функции;
оперировать понятиями: прямая и обратная пропорциональность, линейная, квадратичная функции;
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
строить эскиз графика функции, удовлетворяющей приведенному набору условий;
решать уравнения, неравенства, используя свойства функций и их графиков.
В повседневной жизни и при изучении других учебных предметов:
определять по графикам и использовать для решения прикладных задач свойства реальных процессов и зависимостей;
интерпретировать свойства в контексте конкретной практической ситуации;
определять по графикам простейшие характеристики периодических процессов в биологии, экономике, музыке, радиосвязи и др. (амплитуда, период и т.п.).
Изучение алгебры способствует формированию у обучающихся личностных, метапредметных, предметных результатов обучения, соответствующих требованиям образовательного стандарта среднего общего образования.
Личностные результаты:
воспитание гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;
формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;
ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
осознанный выбор будущей профессиональной деятельности на базе ориентирования в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;
умение управлять своей познавательной деятельностью;
умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно-полезной, учебно-исследовательской, проектной и других видах деятельности;
8) критичность мышления, инициатива, находчивость, активность при решении математических задач [7].
Метапредметные результаты:
умение самостоятельно определять цели своей деятельности, ставить и
формулировать для себя новые задачи в учёбе;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания;
владение навыками познавательной, учебно-исследовательской и проектной деятельности;
формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
формирование компетентности в области использования информационно-коммуникационных технологий;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
11) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом [7].
Предметные результаты:
осознание значения математики для повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
умение описывать явления реального мира на математическом языке; представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления;
представление об основных понятиях, идеях и методах алгебры;
владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач;
владение навыками использования компьютерных программ при решении математических задач [7].
Задания могут иметь различную сложность реализации, но все должны быть построены по одной дидактической схеме.
Принято выделять следующие основные типы уроков:
урок изучения нового материала;
уроки развития и закрепления умений и навыков;
урок контроля знаний;
обобщающий урок;
комбинированный урок.
Качество любого урока в значительной мере определяется тщательностью подготовки к нему учителя. Современные требования к уроку состоят в следующем:
1. Урок предусматривает реализацию в комплексе образовательной, развивающей и воспитывающей функции обучения. Воздействует на все стороны формирования ученика: пополняет запас знаний, развивает умственные силы и способности, формирует мировоззрение, нравственные, эстетические, волевые черты личности, отношение к труду.
2. Урок по форме проведения имеет строгую систему построения: определенное начало, постановку целей и задач урока, объяснение, закрепление или повторение, учебное домашнее задание. Части урока должны быть взаимосвязаны, следовать одна за другой.
3.Урок соответствует принципам обучения: он оказывает воспитывающее влияние, является научным, доступным, способствует прочному и осознанному усвоению материала, формированию умений и навыков.
4.Содержание урока соответствует учебной программе и является звеном в системе других уроков. Всегда нужно думать о том, какое содержание изучено ранее и что будут изучать школьники после данного урока. И не только помнить и знать, но и создавать в учебной деятельности тенденции к предварительному знакомству с некоторыми идеями, которые будут изучаться в дальнейшем.
5. При подготовке и проведении урока учитывается современные психолого–педагогические и методические подходы к обучению и воспитанию [7].
Подготовку учителя к уроку схематично можно представить следующим образом.
1-й этап − изучение учебной программы. При этом особое внимание обращают на основные цели и задачи учебного предмета в целом и на цели и задачи, стоящие перед каждой учебной темой. Готовясь к изучению с учащимися очередной темы, учитель вновь обратится к программе, для того чтобы четко поставить перед собой цели и задачи, которые необходимо достигнуть и решить в процессе изучения темы в целом и на каждом конкретном уроке. Изучая содержание конкретной учебной темы, учитель уяснит логическую взаимосвязь учебного материала с ранее изученным, а также с материалом, который предстоит изучить позже. Это позволит более глубоко и четко сформулировать ближние и дальние цели изучения учебного материала.
2-й этап − изучение методической литературы. Изучив содержание очередной учебной темы по программе, учитель просматривает соответствующие разделы стабильного учебника, методических руководств и статьи в методических журналах, собирает материал для общего плана изучения темы (тематическое планирование). Тематический план не должен быть громоздким. В нем предусматривается самое важное и существенное, а именно: разбивка учебного материала по урокам, логическая взаимосвязь материала, календарные сроки проведения уроков (по неделям).
3-й этап − изучение материала конкретного урока в стабильном учебнике. Изучая учебник, учитель мысленно соотносит характер и логику изложения в нем учебного материала с достигнутым уровнем подготовки и уровнем развития своих учеников. Особенно большое внимание он уделяет доступности изложения учебного материала, отмечает то, что в учебнике изложено просто и доступно, с тем, чтобы часть материала поручить учащимся для самостоятельного изучения. Одновременно надо отметить и то, что может оказаться труднодоступным для учащихся. Особенно тщательно продумывается методика изложения этих вопросов на уроке.
4-й этап − изучение и подготовка имеющихся в школе средств обучения по теме урока. Учитель знакомится не только с имеющимися пособиями, просматривает учебные диафильмы и кинофильмы, но и с аннотациями учебных телевизионных передач, прослушивает звуковые пособия. Ничто так не подрывает авторитета учителя, как неудача в постановке учебного эксперимента. Определяя цели, непременно надо учитывать четыре возможные цели урока − усвоение знаний, привитие навыков и умений, развитие творческого опыта и воспитание. Цели следует обозначать конкретно в соответствии с темой, в зависимости от типа урока, но воспитательную надо иметь в виду всегда. Сообразно целям темы следует намечать упражнения, творческие задачи, конструируя их, если их нет в пособиях.
5-й этап − разработка плана урока. План урока − это конечный результат подготовительной работы учителя к проведению урока. План урока составляется на основе тематического плана с учетом реального продвижения в изучении темы.
В ходе выполнения этой работы для каждого урока разрабатывался:
План урока.
Презентация.
Раздаточный материал.
Выполнены следующие поурочные разработки по теме «Степенная функция»:
Урок 1. Степенная функция, ее свойства и график.
Урок 2. Степенная функция, ее свойства и график.
Урок 3. Взаимно обратные функции.
Урок 4. Взаимно обратные функции.
Урок 5. Равносильные уравнения.
Урок 6. Равносильные неравенства.
Урок 7. Решение задач.
Урок 8. Контрольная работа «Степенная функция, ее свойства и график».
Урок 9. Анализ контрольной работы.
Данный методический продукт предназначен как для начинающих педагогов, так и для учителей, имеющих большой опыт работы. Он позволяет эффективнее использовать время учителя, как на уроке, так и при подготовке к уроку. В представленных далее разработках сделан акцент на практическое применение знаний учащихся, полученных в процессе обучения. Об этом свидетельствует подобранное большое количество практических упражнений на каждом уроке.
ВЫВОДЫ
Исходя из поставленных задач можно сделать следующие выводы:
Определены планируемые результаты изучения обучающимися темы «Степенная функция».
Изучены требования к предметным результатам освоения курса математики. В результате были выделены основные требования:
- сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления; владение основными понятиями о степенных функциях, их основных свойствах и графиках, о равносильных уравнениях и неравенствах, взаимно обратных функциях;
- сформированность умения читать графики и описывать их свойства, определять взаимно обратные функции, равносильные уравнения и неравенства;
- применять изученные свойства для решения математических задач и задач с практическим содержанием
Уровень обязательной подготовки учащихся по теме «Степенная функция» включает в себя следующие требованиями:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
решать уравнения и неравенства с параметрами.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов.
3. На примере учебника «Алгебра и начала математического анализа». 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровень / Ш.А. Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016. были рассмотрены основные требования к знаниям, умениям, навыкам приобретаемым учащимися при изучении темы «Степенная функция», а также определены цели обучающегося и учителя при изучении данной темы.
4. В работе рассмотрены основные вопросы по методике обучения теме «Степенная функция», включенные в курс алгебры общеобразовательной школы и составлены методические рекомендации по данной теме.
5. Разработан цикл уроков по теме «Степенная функция».
Цель исследования достигнута.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Закон Донецкой Народной Республики «Об образовании», утвержденный Постановлением №I – 233П – НС Народного Совета Донецкой Народной Республики от 19 июня 2015 г.
Базисный учебный план для общеобразовательных организаций Донецкой Народной Республики.
Государственные образовательные стандарты среднего общего образования (Приказ МОН ДНР от 07.08.2020 г. № 121-НП).
Примерная основная образовательная программа среднего общего образования (Приказ МОН ДНР от 26.08.2020 г. № 1182).
Примерная программа по учебному предмету «Алгебра и начала математического анализа». 10-11 классы (базовый, углубленный уровни) / сост. Скафа Е.И., Федченко Л.Я., Полищук И.В. – 5-е изд. перераб., дополн. – ГОУ ДПО «ДонРИДПО». – Донецк: Истоки, 2020. – 52 с.
Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровень / Ш.А. Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.
С. Пути повышения эффективности и качества уроков математики в средней школе. https://topref.ru/referat/126341/3.html
Малова И.Е., Горохова С.К. и др. Теория и методика обучения математике в средней школе. https://may.alleng.org/d/math/math2471.htm
Колягин Ю.М., учебное пособие «Методика преподавания математики в средней школы: Частные методики» Колягин Ю.М., Луканкин Г.Л., Мокрушин Е.Л. и др. - М.: Просвещение, 1977. — 480 с.
Холодулина, С.Ю. Методика обучения функциям в курсе алгебры основной школы/ С.Ю. Холодулина: бакалаврская работа по направлению подготовки «Педагогическое образование», направленность (профиль) «Математика и информатика». – Тольятти, ТГУ. – 2017. – 122 с.
Из истории функций. http://graphfunk.narod.ru/history.htm
Федченко Л.Я., Разноуровневые задания для тематических и итоговых контрольных работ по алгебре. 10-11 классы. / Л.Я. Федченко, Г.Н. Литвиненко. - Д., 2008. – 112 с.
Алгебра и начала математического анализа: учебник для 10-11 кл. сред. шк. / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; под ред. А.Н. Колмогорова. – 2-е изд. - М.: Просвещение, 1991.
Крамор В.С. Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Провсещение, 1990.
Симонов А.Я., Система тренировочных задач и упражнений по математике/ А.Я. Симонов, Д.С. Бакаев, А.Г. Эпельман и др. – М.: Просвещение, 1991.
Тымко Ю.Г., статья в журнале, «Подготовка будущего учителя математики к работе по формированию понятий у учащихся в рамках курса "Методика обучения математике". https://seanewdim.com.
ТЕМА 2. СВОЙСТВА СТЕПЕННОЙ ФУНКЦИИ. УРАВНЕНИЯ И НЕРАВЕНСТВА (9 ЧАСОВ)
Урок № 1 Дата: 10 класс
Тема: Степенная функция, ее свойства и график.
Цели урока:
предметные – представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления;
метапредметные – умение самостоятельно определять цели своего обучения, ставить для себя новые задачи, акцентировать мотивы и развивать интересы своей познавательной деятельности; умение планировать, контролировать и объективно оценивать свои учебные и практические действия в соответствии с поставленной задачей и условиями её реализации; самостоятельно оценивать уровень сложности заданий (упражнений) в соответствии с возможностями своего организма; формулировать, аргументировать и отстаивать своё мнение, умение вести дискуссию, обсуждать содержание и результаты совместной деятельности;
личностные – готовность и способность к саморазвитию и самообучению; ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно-полезной, учебно-исследовательской, проектной и других видах деятельности.
Задачи урока:
Систематизировать и расширить знания по теме «Степенная функция», познакомить учащихся со свойствами и графиками различных (в зависимости от показателя степени) видов степенной функции, формирование функциональных представлений на наглядном материале, формирование умений построения графиков степенных функций, при различных значениях показателя степени, формировать навыки свободного чтения графиков, умение отражать свойства функции на графике.
Формирование способности анализировать, обобщать полученные знания. Формирование логического мышления.
Активизировать интерес к получению новых знаний, воспитание графической культуры, формирование точности и аккуратности при выполнении чертежей.
Тип урока: изучение нового материала.
Вид урока: исследовательская работа.
Методы и приемы обучения: объяснительно-иллюстративный; частично-поисковый; словесный (фронтальная беседа); наглядный (демонстрация компьютерной презентации); практический.
Формы организации учебной деятельности: фронтальная, групповая, индивидуальная.
Средства обучения: авторская презентация; учебник Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровень / Ш.А. Алимов, Ю.М. Колягин и др. – М.: Просвещение, 2016.); технические (компьютер, мультимедийный проектор), рабочая тетрадь, чертёжные инструменты; опорный конспект темы, набор графиков и формул функций
В результате изучения темы учащиеся должны
Знать: применение степенной функции, свойства степенной функции в зависимости от показателя.
Уметь: называть свойства степенной функции в зависимости от показателя, строить графики (эскизы графиков) степенных функций с рациональным показателем, выполнять преобразования графиков, уметь четко и ясно излагать свои мысли, анализировать, делать выводы.
![]() Слайд 4
Слайд 4
План урока:
1.Организационный момент. (1 минута)
2. Актуализация знаний. (5 минут)
3. Изложение нового материала. (20 минут)
4. Физкультминутка. (2 минуты)
5. Первичное закрепление. (10 минут)
6. Проверка усвоения новых знаний. (5 минут)
7. Итог. Рефлексия (1 минута)
8. Домашнее задание. (1 минута)
ХОД УРОКА
I. Организационный момент. Сообщение темы и целей урока.
- Приветствие.
- Организация рабочих мест.
- Проверьте ваши рабочие места: учебник, рабочая тетрадь, ручка.
![]() Слайд 5 Эпиграф урока
Слайд 5 Эпиграф урока
| Как алгебраисты вместо АА, ААА, … пишут А2, А3, так я…. вместо И. Ньютон | |
Как Вы понимаете эти слова? (Учащиеся дают ответы).
Тема сегодняшнего урока «Степенная функция, ее свойства и график». Исходя из темы попробуйте сформулировать цели нашего урока.
- Данная тема новая для вас?
II. Актуализация опорных знаний учащихся.
Чтобы действительно себя настроить на работу на уроке, проверим свои знания с помощью теста.
![]() Слайд 6 Тест на 2 варианта (время выполнения — 5 минут).
Слайд 6 Тест на 2 варианта (время выполнения — 5 минут).
Вариант 1
1.Найдите значение выражения: 6∙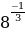 .
.
1) 12; 2) 6; 3) 3; 4) –3.
2. Представьте данное выражение в виде степени: у1,7∙ у2,8 ∙ у-1,5.
1) у -3; 2) у -7,14; 3) у 3; 4) у 6.
3. Упростите выражение: 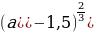 .
.
1) а; 2) 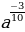 ; 3)
; 3) 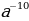 ; 4)
; 4) 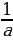
4. Упростите выражение: b-0,2 : b-0,7.
1) 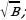 2)
2) 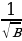 ; 3) b –0,9; 4) b2/7.
; 3) b –0,9; 4) b2/7.
5. Найдите сумму корней уравнения х + 1 = 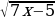 .
.
1) –1; 2) 1; 3) 4; 4) 5.
Вариант 2
1. Найдите значение выражения: 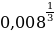 .
.
1) 0,016; 2) 0,0016; 3) 0,2; 4) 0,04.
2. Упростите выражение:  .
.
1) х –2,9; 2) х –2,1; 3) х; 4) 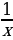 .
.
3. Упростите выражение: d 1,8 : d -2.
1) d -0,9; 2) d 3,8; 3) d–0,2; 4) d 0,2.
4. Найдите значение выражения: 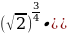 .
.
1) 4; 2) 2; 3) 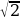 ; 4) 2
; 4) 2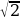 .
.
5. Найдите произведение корней уравнения х + 1 = 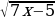 .
.
1) –1; 2) 6; 3) 4; 4) 5.
![]() Слайд 7 Проверка тестов. Скажите, какие задания вызвали у вас затруднения при решении?
Слайд 7 Проверка тестов. Скажите, какие задания вызвали у вас затруднения при решении?
| 1 вариант | | 2 вариант | ||||||||
| 1 | 2 | 3 | 4 | 5 | | 1 | 2 | 3 | 4 | 5 |
| 3 | У3 | 1/а |
| 5 | | 0,2 | 1/х | | 2 | 6 |
Итак, цель сегодняшнего урока: систематизировать и расширить знания по теме «Степенная функция»…. .
III. Изложение нового материала.
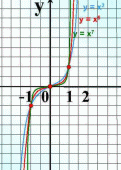
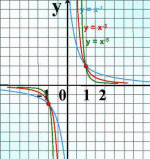
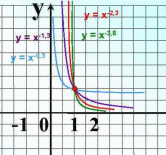
Начиная с седьмого класса мы изучили множество функций, графики которых вы видите на слайде. Назовите эти функции. Что их все объединяет?
|
у = х, прямая пропорциональность, k = 1, графиком функции является прямая, проходящая через начало координат. |
|
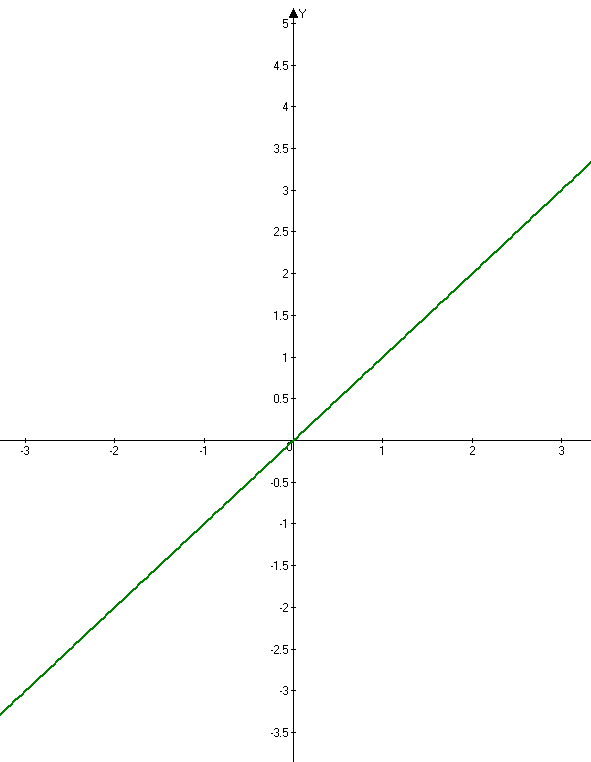
| у = х2, квадратичная функция, графиком является парабола. |
|
|
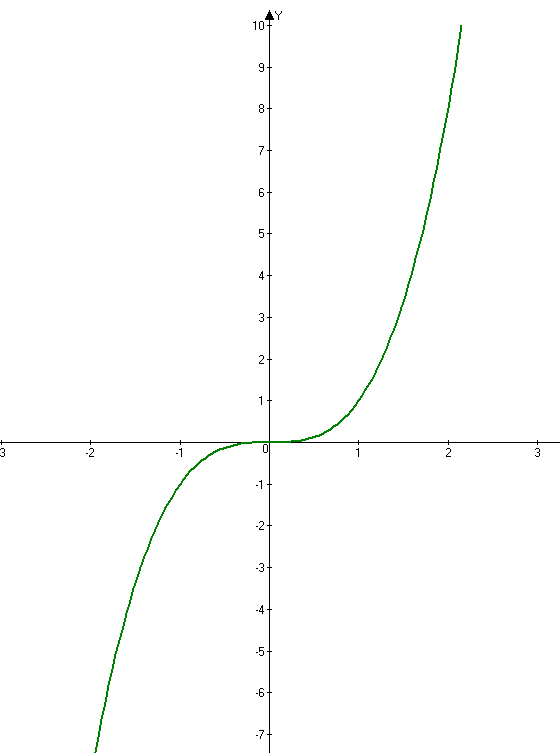
у = х3, кубическая функция, графиком функции является кубическая парабола. |
|
| у =
|
|
| у = |
|
Согласитесь ли вы со мной, что все эти функции являются частными случаями степенной функции?
![]() Слайд 10 Определение:
Слайд 10 Определение:
Функция вида у = хр, где р – заданное действительное число, называется степенной функцией.
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень хр.
Скажите, пожалуйста, а какие основные свойства функций мы обычно указываем?
1.Область определения. (все значения которые принимает аргумент х).
2.Область значений (множество значений). (все значения, которые принимает функция у).
3.Четность, нечетность функции. Графическая иллюстрация четной, нечетной функции. (симметрична относительно Ох, Оу). Аналитическая запись свойства четности, нечетности. (f(x)= f(-x); f(x)=- f(x))
4.Записываем промежутки возрастания и убывания функции. (как определить по графику?)
5.Записываем промежутки знакопостоянства (у 0, y
![]() Слайд 11 Сегодня на уроке мы познакомимся с новыми для Вас свойствами.
Слайд 11 Сегодня на уроке мы познакомимся с новыми для Вас свойствами.
Определение 1. Функция у = f(х), определенная на множестве Х, называется ограниченной снизу на множестве Х, если существует число а такое, что для любого х ϵ Х выполняется неравенство f(х) ≥ а.
| Пример: |
|
Определение 2. Функция у = f(х), определенная на множестве Х, называется ограниченной сверху на множестве Х, если существует число А такое, что для любого х ϵ Х выполняется неравенство f(х) ≤ А.
| Пример: |
|
Определение 3. Функцию, ограниченную и сверху, и снизу на множестве Х, называют ограниченной на этом множестве.
| Пример: |
|
Перейдем к подробному рассмотрению различных случаев графиков степенной функции у = хр в зависимости от показателя степени р.
Новый материал можно записать в виде таблицы:
![]() Слайд 12
Слайд 12
| Показатель р = 2n – четное натуральное число. Например: у = х2, у = х4, у = х6, у = х8, ….. | |
|
| Свойства: 1)D(у): хꞓR. 2)Е(у): у≥0. 3)Функция четная, т.к. (-х)2n = x2n. 4)Убывает, если х≤0, возрастает, если х≥0. 5)Функция ограничена снизу. 6)Наименьшее значение у = 0 при х = 0. Наибольшего значения нет. |
![]() Слайд 13
Слайд 13
| Показатель р = 2n - 1 – нечетное натуральное число. Например: у = х3, у = х5, у = х7, у = х9, ….. | |
|
| Свойства: 1)D(у): хꞓR. 2)Е(у): уꞓR. 3)Функция нечетная, т.к. (-х)2n-1 = - x2n-1. 4)Возрастает на всей области определения. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет.
|
![]() Слайд 14
Слайд 14
| Показатель р = - 2n – где n - натуральное число. Например: у = х-2 = | |
|
| Свойства: 1)D(у): х≠0. 2)Е(у): у0. 3)Функция четная, т.к. 4)Возрастает при х 0. 5)Функция ограниченна снизу. 6)Наибольшего и наименьшего значения нет. |
![]() Слайд 15
Слайд 15
| Показатель р = -(2n – 1) – где n - натуральное число. Например: у = х-1 = | |
|
| Свойства: 1)D(у): х≠0. 2)Е(у): у≠0. 3)Функция нечетная, т.к. 4) Убывает при х 0. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет. |
![]() Слайд 16
Слайд 16
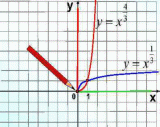
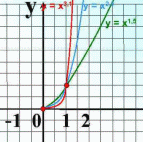
| Показатель р – положительное действительное нецелое число. Например: у = | |
|
| Свойства: 1)D(у): х≥0. 2)Е(у): у≥0. 3)Функция ни четная, ни нечетная. 4)Возрастает, если х≥0. 5)Функция ограничена снизу. 6)Наименьшее значение у = 0 при х = 0. Наибольшего значения нет. |
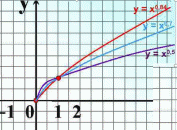
![]() Слайд 17 Примеры показательной функции, где р – положительное действительное нецелое число.
Слайд 17 Примеры показательной функции, где р – положительное действительное нецелое число.
|
|
|
![]() Слайд 18
Слайд 18
| Показатель р – отрицательное действительное нецелое число. Например: у = | |
|
| Свойства: 1)D(у): х0. 2)Е(у): у0. 3)Функция ни четная, ни нечетная. 4)Убывает, если х0. 5)Функция ограничена снизу. 6)Наименьшего и наибольшего значения нет.
|
![]() Слайд 19
Слайд 19
IV. Физкультминутка.
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни Вершиной вниз.
И вновь глазами ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы наконец.
Зарядка окончилась. Ты молодец!
(Дети представляют внешний вид геометрических фигур.)
![]() Слайд 20
Слайд 20
V.Первичное закрепление ЗУНов.
№120. (Устно). Выяснить, являчется ли функция у = хр возрастающей (убывающей) при х 0, если:
| р = 7 | р = 16 | р = -3 | р = -7 | р = -4 | р = -10 |
| Возрастает | Возрастает | Убывает | Убывает | Убывает | Убывает |
№119 (1,3,5) – работа у доски.
у = х6.
Решение:
|
| Свойства: 1)D(у): хꞓR. 2)Е(у): у≥0. 3)Функция четная, т.к. (-х)6 = x6. 4)Убывает, если х≤0, возрастает, если х≥0. 5)Функция ограничена снизу. 6)Наименьшее значение у = 0 при х = 0. Наибольшего значения нет.
|
![]() Слайд 21
Слайд 21
у = х7.
|
| Свойства: 1)D(у): хꞓR. 2)Е(у): уꞓR. 3)Функция нечетная, т.к. (-х)7 = - x7. 4)Возрастает на всей области определения. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет.
|
![]() Слайд 22
Слайд 22
у = х-3.
|
| Свойства: 1)D(у): х≠0. 2)Е(у): у≠0. 3)Функция нечетная, т.к. 4) Убывает при х 0. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет.
|
![]() Слайд 23
Слайд 23
VI. Проверка усвоения новых знаний.
№123. Построить график функции у = - (х-2)3 – 1, сформулировать свойства данной функции.
| у = - (х-2)3 – 1 Свойства: 1)D(у): хꞓR. 2)Е(у): уꞓR. 3)Функция ни четная, ни нечетная. 4)Убывает на всей области определения. 5)Функция не является ограниченной. 6)Наибольшего и наименьшего значения нет.
|
|
![]() Слайд 24
Слайд 24
VI. Итог урока. Рефлексия.

VII. Оценивание. Домашнее задание.
Выучить §6, стр.39. Решить №119 (2,4,6), 123 (б).
Самостоятельная работа
Установить соответствия между функциями и их обастью определения:
1 вариант 2 вариант
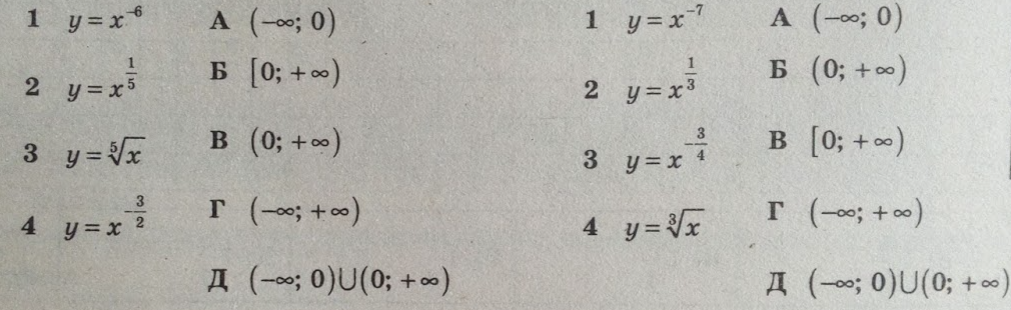
Установить соответствия между функциями и их графиками:
3 вариант 4 вариант
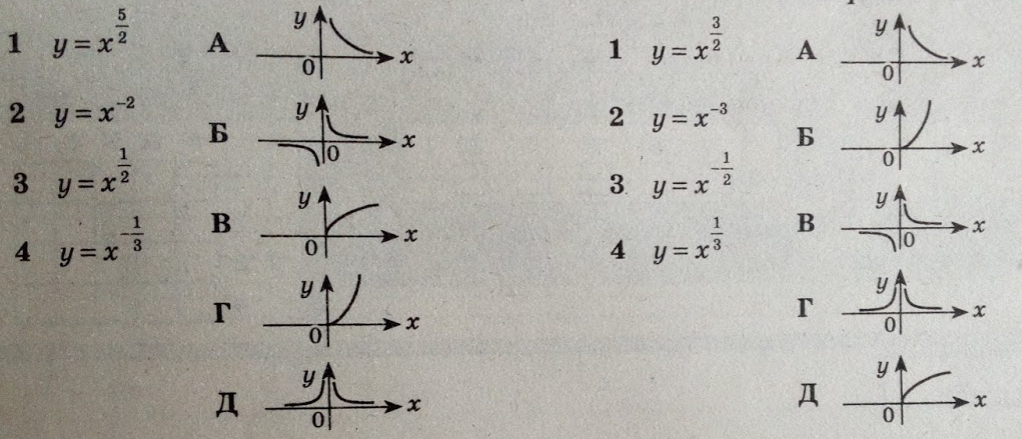
ОТВЕТЫ
| № | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| 1 | Д | Д | Г | Б |
| 2 | Б | В | Д | В |
| 3 | Г | Б | В | А |
| 4 | В | Г | А | Д |






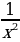 , у = х-4 =
, у = х-4 = 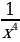 , у = х-6 =
, у = х-6 = 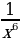 , у = х-8 =
, у = х-8 =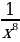 , …..
, …..
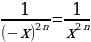 .
.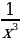 , у = х-5 =
, у = х-5 =  , у = х-7 =
, у = х-7 = 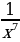 , …..
, …..
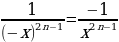 .
.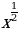 , у =
, у = 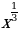 ,
, 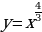 , ….
, ….
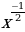 , у =
, у = 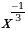 ,
, 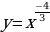 , ….
, ….
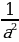 ,
,  ,….. пишу а-1, а-2, а-3,……
,….. пишу а-1, а-2, а-3,……
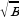
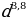
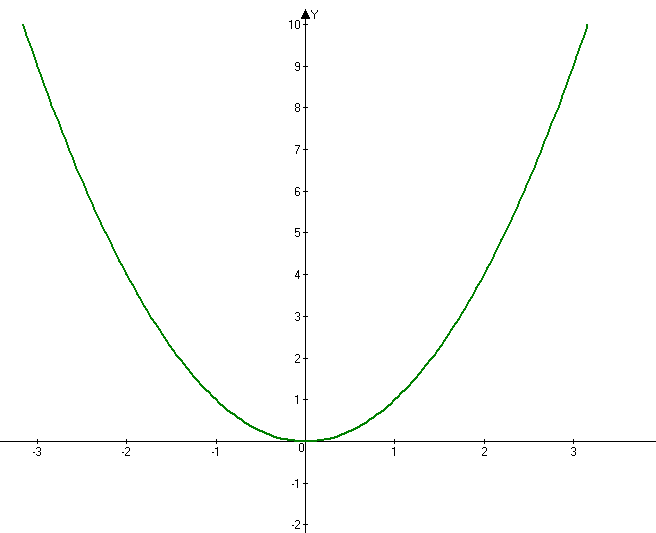
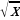 - графиком функции является ветвь параболы.
- графиком функции является ветвь параболы.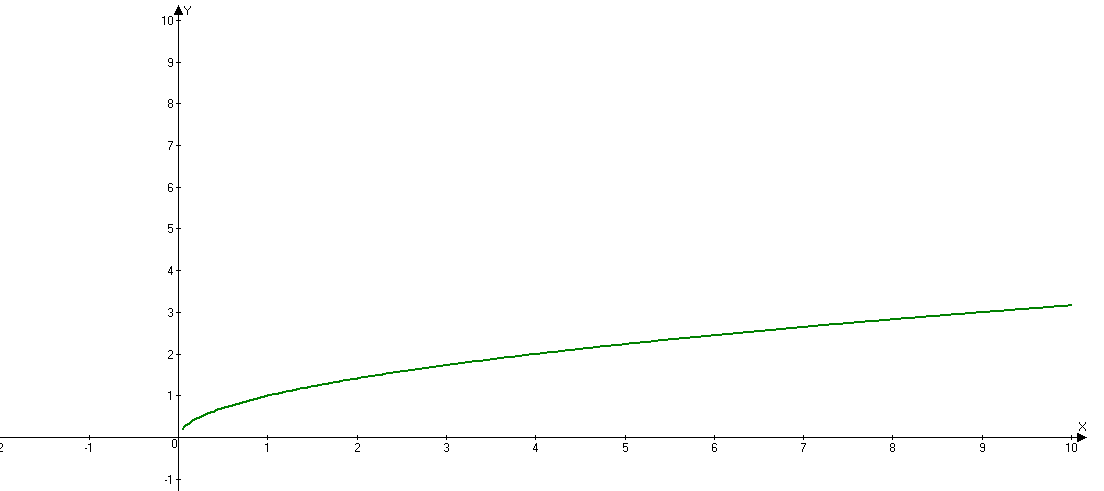
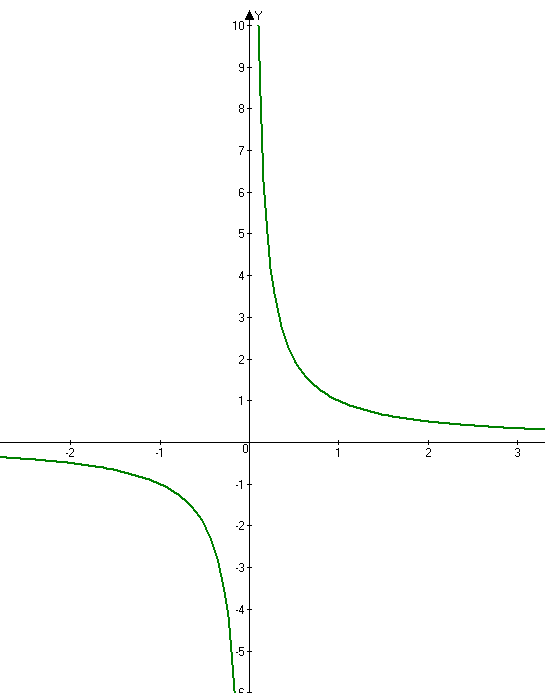
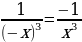 .
.