Разработка обобщающего урока по теме "Тригонометрия"

Алгебра и начала анализа

10 класс

(«три» - три, «гониа» - угол, «метриа» - измеряю)

раздел математики, изучающий соотношение сторон и углов в треугольнике

Функция ( отображение , оператор , преобразование ) — математическое понятие, отражающее связь между элементами множеств. Другими словами, функция — это правило, по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Викпендия

Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости сторон этих треугольников от острых углов при гипотенузе.

Эти функции нашли широчайшее применение в самых разных областях науки.

прямые тригонометрические функции

синус (sin x)

косинус (cos x)

производные тригонометрические функции

тангенс (tg x)

котангенс (ctg x)

Обобщить и систематизировать знания по теме «Тригонометрические функции»

• Что такое числовая окружность?

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

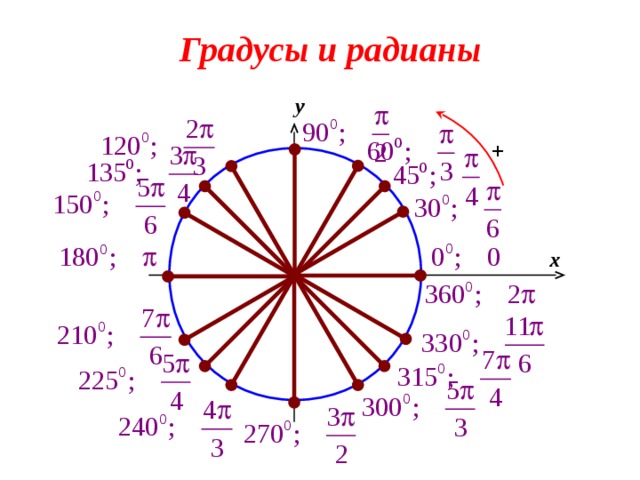
Градусы и радианы

y

+

x

0

9

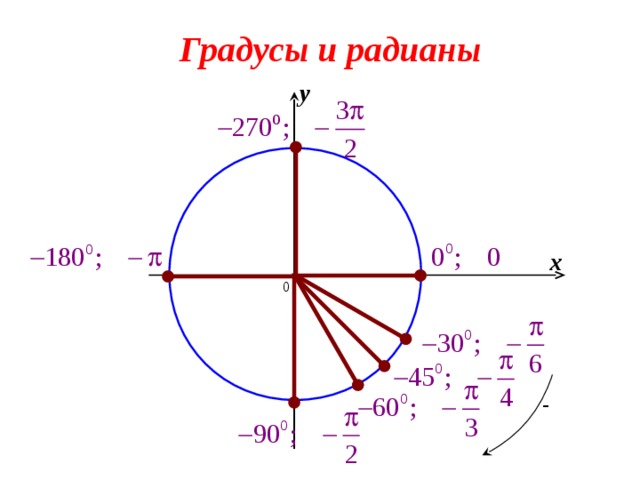
Градусы и радианы

y

x

0

-

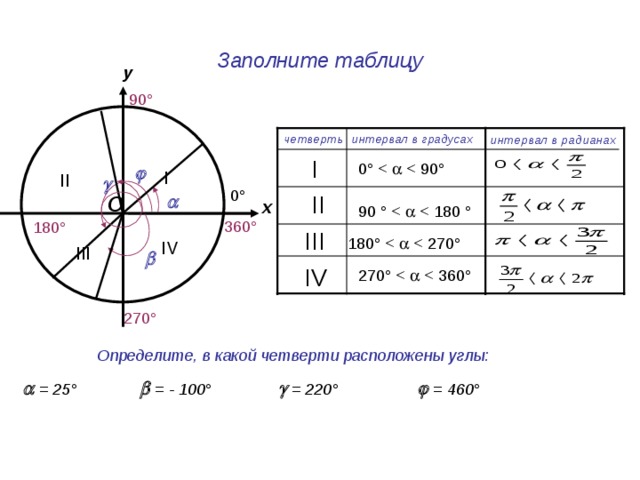
Заполните таблицу

у

90°

интервал в градусах

интервал в радианах

четверть

I

0°



I

II



0°

II

О



х

90 °

360°

180°

III

180°

IV

III



IV

270°

270°

Определите, в какой четверти расположены углы:

 = 220°

 = 25°

 = - 100°

 = 460°

• y = sin 2x
• y = 3cos x + x
• y= 4tg x

• y = sin 2x
• y = 5sin x
• y = 4tg x

• Дана функция: y = sin 2x
• Вычислить:
• А) у (0)
• Б) у (п/2)
• В) у (п)

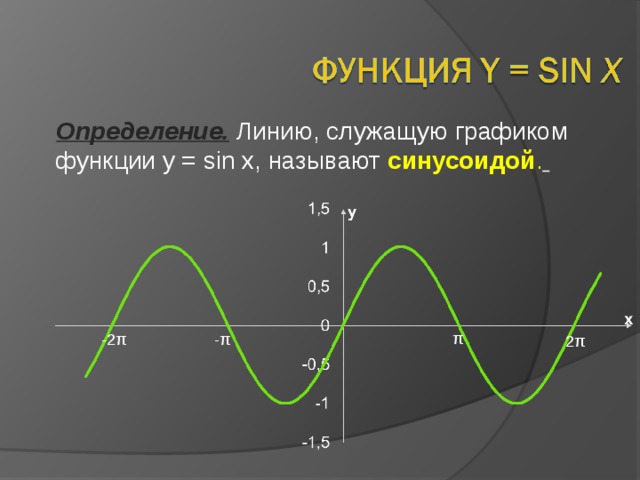
Определение. Линию, служащую графиком функции y = sin x , называют синусоидой .

π

-π

-2π

2π

11

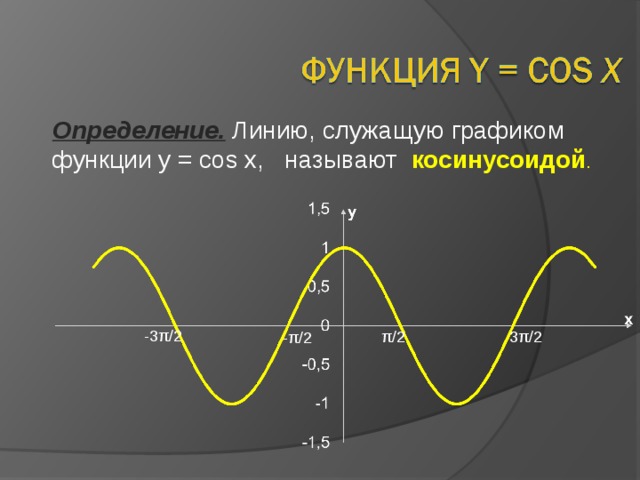
Определение. Линию, служащую графиком функции y = cos x , называют косинусоидой .

-3π/2

3π/2

π/2

-π/2

11

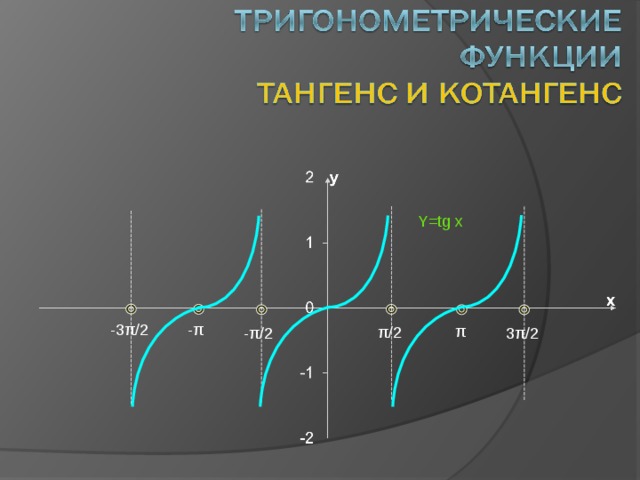
Y=tg x

-π

-3π/2

π

π/2

-π/2

3π/2

17

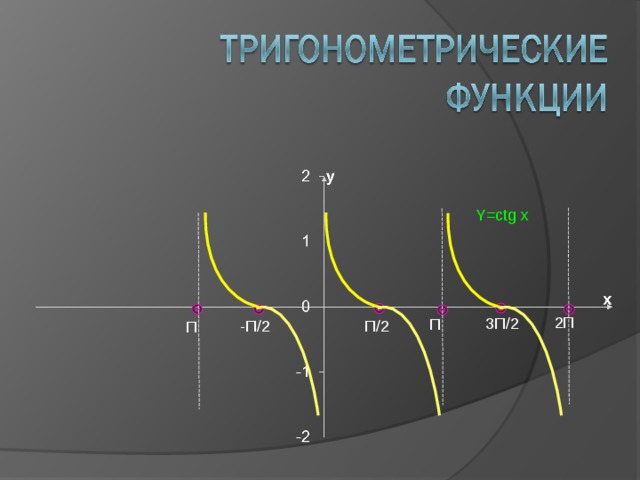
Y=ctg x

2П

3П/2

П

П/2

-П/2

П

18

Сегодня мы познакомимся с фрагментами биографии одной известной женщины-математика, у которой девизом всей жизни было: «служить истине, служить справедливости». Но знакомиться мы будем в результате выполнения учебных  заданий по теме сегодняшнего урока.

Кто же эта женщина? Выберите её имя из четырёх имён известных женщин, каждому из которых соответствует набор из единиц и нулей. Правильному ответу на вопрос соответствует набор, имеющий некоторое отличительное свойство  по сравнению с другими наборами.

«В истории человечества до Ковалевской не было женщины, равной ей по силе

и своеобразию математического таланта…».

Академик С.И. Вавилов.

Софья Васильевна Ковалевская

1848

2

1850

1852

1

3

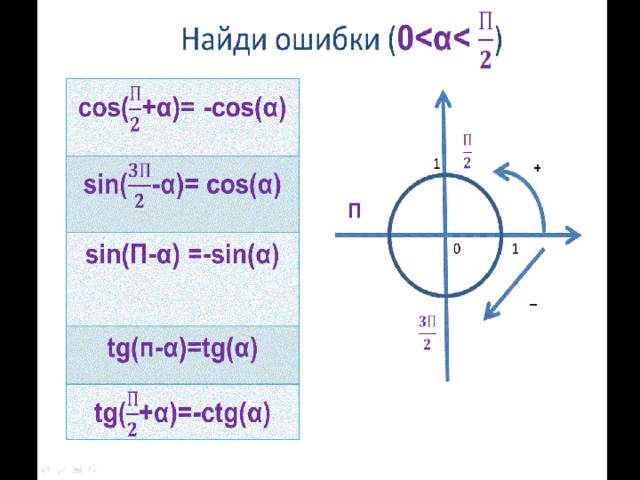
• Выполните задание: «Найди ошибки»

(формулы приведения).В тетрадях.

• Поставьте цель данного этапа урока

цель: повторить формулы приведения

Лошадиное правило

В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус), смотрел на свою умную лошадь. Она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/2 ±а  

(3 π/2 ± а ) или  π ± а (2π ± а). Если лошадь кивала головой вдоль оси ОУ , то математик считал, что получен ответ «да, менять» , если вдоль оси ОХ , то «нет, не менять».

COS ( П/2 + a)= - cos a

! COS ( П/2 + a)= - sin a

Sin( 3 п/2 – а) = со s a

! Sin( 3 п/2 – а) = - со s a

Sin ( п - a)= - sin a

! Sin ( п - a)= + sin a

tg (п – а) = tg a

! tg (п – а) = - tg a

tg ( п/2 +a)= - ctg a

+

1848

3

1850

1852

4

5

Имение Крюковских:

(правильный ответ в таблице)

Карелино

Ливоново

о

Полибино

0,5

Марьино

1

2

• Выполните задание: тест «Тригонометрические функции»
• Поставьте цель данного этапа урока

цель: повторить свойства и графики тригонометрических функций

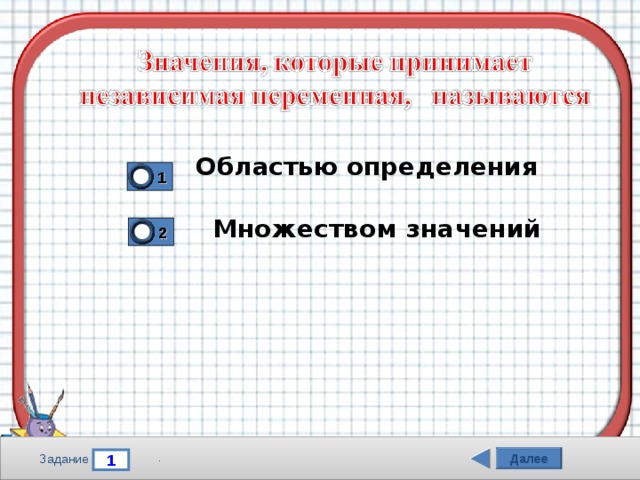
Областью определения

1

Множеством значений

2

Далее

1

Задание

.

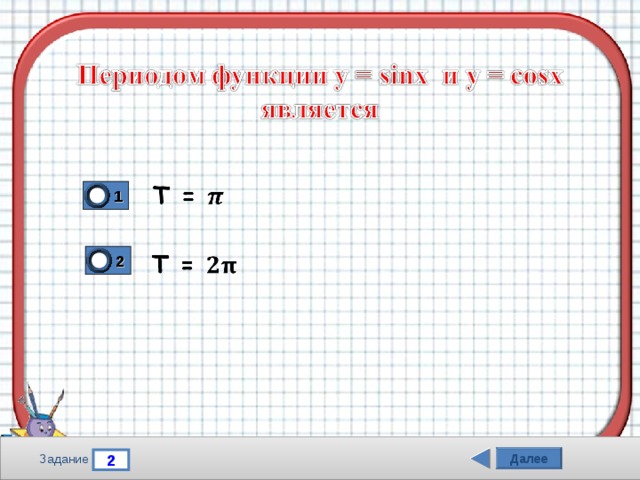
1

2

Далее

2

Задание

  Параллельный перенос вверх (

вниз) вдоль оси ОУ

1

Растяжение (сжатие) вдоль

оси ОУ

2

Параллельный перенос вправо

(влево) вдоль оси ОХ

3

  Растяжение (сжатие) вдоль

оси ОХ

4

Далее

3

Задание

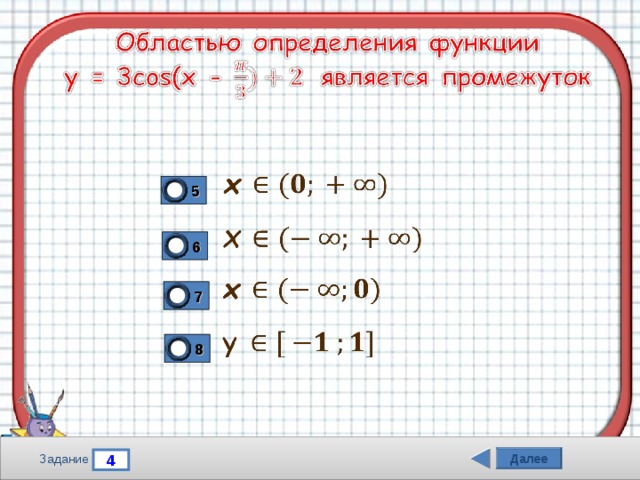
5

6

7

8

Далее

4

Задание

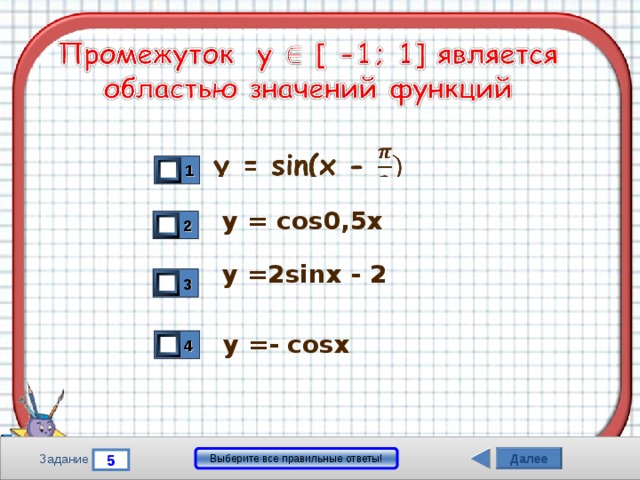
1

y = cos0,5x

2

y =2sinx - 2

3

y =- cosx

4

Далее

Выберите все правильные ответы!

5

Задание

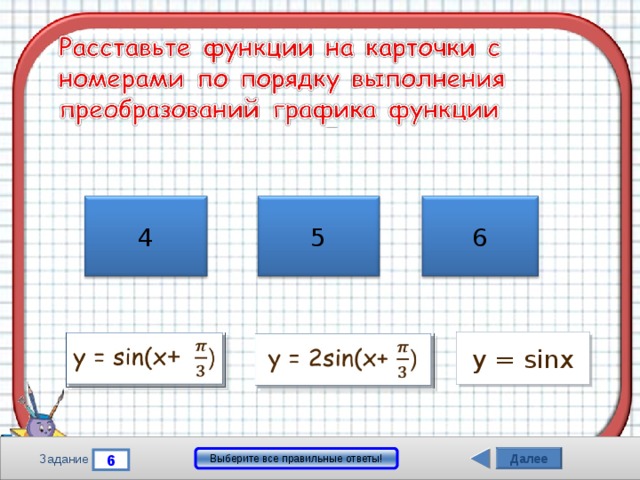
6

5

4

1

3

2

y = sinx

Далее

Выберите все правильные ответы!

6

Задание

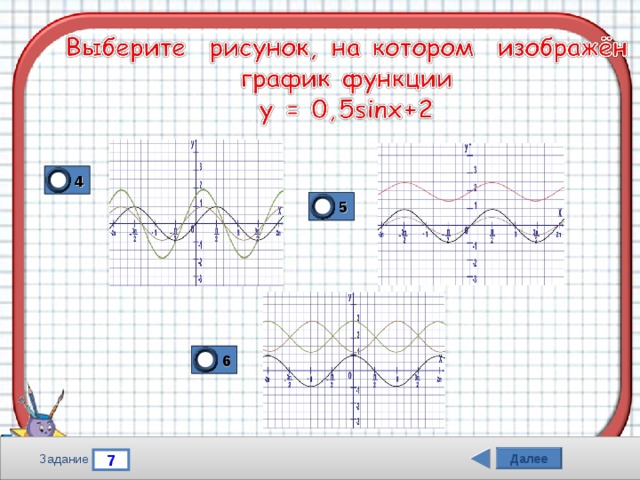
4

5

6

Далее

7

Задание

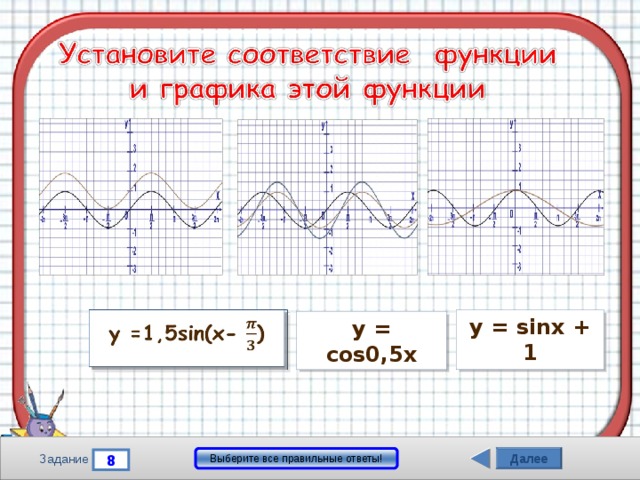
3

2

1

y = sinx + 1

y = cos0,5x

Далее

Выберите все правильные ответы!

8

Задание

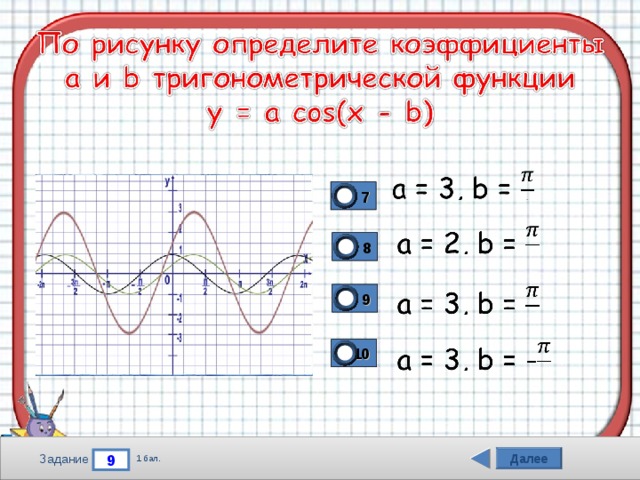
7

8

9

10

Далее

9

Задание

1 бал.

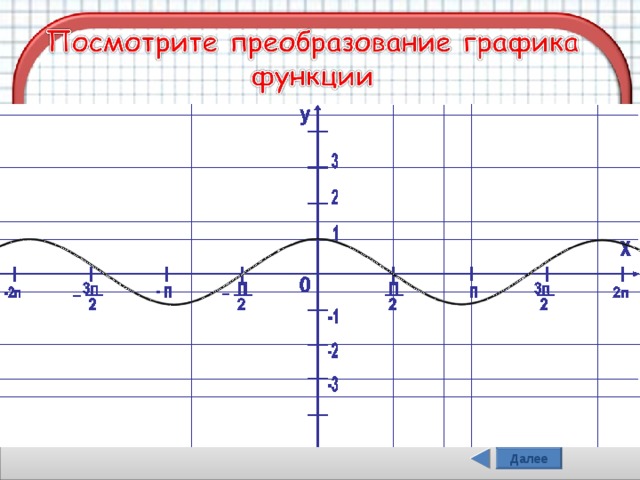
у

3

2

1

х

0

3п

п

п

3п

п

- п

-2п

2п

2

2

2

2

-1

-2

-3

Далее

Задание

у

3

2

1

х

0

3п

п

п

3п

п

- п

2п

-2п

2

2

2

2

-1

-2

-3

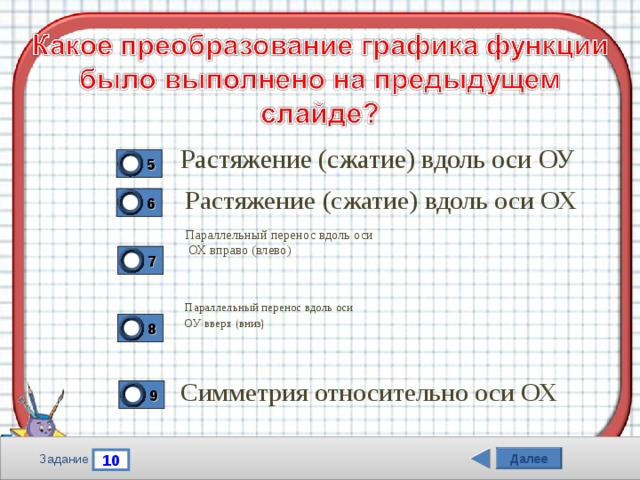
Растяжение (сжатие) вдоль оси ОУ

5

Растяжение (сжатие) вдоль оси ОХ

6

Параллельный перенос вдоль оси

ОХ вправо (влево)

7

Параллельный перенос вдоль оси

ОУ вверх (вниз)

8

Симметрия относительно оси ОХ

9

Далее

10

Задание

Выполнив задания, поставьте в соответствие правильному ответу букву из таблицы.

Вы узнаете ответ на вопрос:

В какой области С. Ковалевская была так же талантлива, как и в математике.

ЛИТЕРАТУРА

Если ты в жизни, хотя на мгновенье

Истину в сердце своём ощутил,

Если луч правды сквозь мрак и сомненье

Ярким сияньем твой путь озарил:

Чтобы в решеньи своём неизменном

Рок ни назначил тебе впереди -

Память об этом мгновеньи священном

Вечно храни, как святыню, в груди

Тучи сберутся громадой нестройной,

Небо покроется чёрною мглой,

С ясной решимостью, и с верной спокойной

Бурю ты встреть и померься с грозой.

Софья Ковалевская

• Достигли ли мы ее?
• Каким образом мы ее достигли.

Спасибо за урок!