У р о к № 1. Плоскость, прямая, луч, угол
Основная дидактическая цель урока: сформировать понятие «плоскость», научить находить и называть прямую на чертеже, строить её по двум точкам.
Х о д у р о к а
I. Организационный момент
– Решив все примеры и расположив ответы в порядке возрастания, вы сможете прочитать два слова, которые являются темой нашего урока. (Плоскость, прямая.)
1) 81 : 9 С 2) 15 ・ 0 П
15 ・ 3 С 17 ・ 10 Я
17 - 9 О 32 : 32 Р
33 + 16 Т 90 : 10 Я
44 ・ 0 П 16 + 14 М
13 ・ 1 К 90 - 30 А
63 : 63 Л
96 ・ 100 Ь
300 : 10 О
II. Работа по теме урока
1. Плоскость
– Прочитайте о плоскости в учебнике на с. 22.
– Какие предметы дают нам представление о плоскости?
– Чем отличаются эти предметы от плоскости?
– Какую важную мысль мы должны запомнить? (У плоскости нет края.)
– Запишите это в тетради.
2. Прямая
– Прочитайте о прямой в учебнике.
– Начертите отрезок АВ.
– Продолжите его по линейке в обе стороны.
Вы получили новую фигуру – прямую, которая обозначается «прямая АВ» или «прямая ВА».
– Что мы должны знать о прямой?
1. Через любые две точки проходит единственная прямая.
2. Прямая не имеет концов.
3. Прямая неограниченно продолжается в обе стороны.
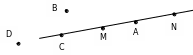
– Какая фигура изображена на рисунке?
– Что вы скажете о точках А, В, С, D? (Точки А, С лежат на прямой.)
– Как проверить, лежит ли на прямой MN точка D? Точка В?
III. Работа по учебнику
– Рассмотрите рис. 1.15.
– Какие фигуры изображены на рисунке? (Прямые АВ и PQ.)
– Принадлежит ли точка М прямой АВ? прямой PQ?
Говорят так: «Прямые АВ и PQ имеют одну общую точку, а следовательно, такие прямые называются пересекающимися».
– Попробуйте сами сформулировать ответ на вопрос: «Какие прямые называются пересекающимися?»
1. С. 23, № 1.93.
– Прямая не имеет начала, не имеет конца.
– Представьте, что все три прямые продолжаются бесконечно.
– Какие прямые имеют точку пересечения?
2. С 24, № 1.95.
– Лежит ли точка М на прямой KL?
3. С. 24, № 1.96.
(МВ, МС, ВС, ВМ, СМ, СВ.)
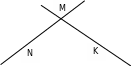 4. С. 24, № 1.99.
4. С. 24, № 1.99.
(Прямые делят плоскость на 7 частей.)
IV. Работа над комбинаторной задачей
1. С. 25, № 1.115.
Задача 1
– Какие величины даны в первой задаче?
– Прочитайте условие задачи, убрав из вопроса числовое данное.
– Что надо узнать в задаче?
– Как найти скорость?
– Составьте план решения задачи.
– Решите задачу.
1) 6 ・ 10 = 60 (км) – расстояние.
2) 60 : 4 = 15 (км/ч) – искомая скорость.
– Прочитайте ответ. (Скорость велосипедиста 15 км/ч.)
Задача 2
– Вторую задачу решите самостоятельно.
1) 3 ・ 16 = 48 (км) – расстояние.
2) 48 : 12 = 4 (ч) – искомое время.
– Прочитайте ответ. (Моторной лодке потребуется 4 ч.)
2. С. 25, № 1.114.
– Прочитайте задачу.
– Что вы можете о ней сказать?
– Рассмотрим решение задачи.
– Сколькими способами можно выбрать скипа?
– Сколько различных вариантов выбора вице-скипа существует для каждого возможного выбора президента?
– Сколько же способов существует? (3 ・ 4 = 12.)
V. Работа в рабочей тетради
С. 12, № 2, 3.
VI. Рефлексия
– Отвечаем на вопросы на с. 23 после теоретической части.
Домашнее задание
С. 25, № 1.117; с. 26, № 1.119, 1.121.







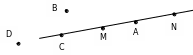
 4. С. 24, № 1.99.
4. С. 24, № 1.99.









