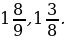У р о к № 1. Сокращение дробей
Основная дидактическая цель урока: ввести понятие «сокращение дробей≫ и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби; отрабатывать умение решать задачи на движение по воде; развивать умение самостоятельно мыслить.
Х о д у р о к а
I. Организационный момент
– Ребята, какую тему вы изучали на прошлых уроках? (Основное свойство дроби.)
– Что вы уже узнали? (Основное свойство дроби. Числитель и знаменатель можно умножать и делить на одно и то же натуральное число.)
Сегодня вы продолжите работать с основным свойством дроби.
II. Работа по теме урока
1. Числитель и знаменатель дроби 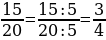 мы сможем разделить на одно и то же число, воспользовавшись основным свойством дроби. В дальнейшем это преобразование будем называть сокращением дроби.
мы сможем разделить на одно и то же число, воспользовавшись основным свойством дроби. В дальнейшем это преобразование будем называть сокращением дроби.
2. Определение сокращения дроби.
Сократить дробь – означает разделить её числитель и знаменатель на одно и то же число (не равное нулю). В результате получаем равную дробь, но с меньшими числителем и знаменателем.
3. При сокращении дроби изменится лишь её запись, числовое значение дроби не меняется.
4. Дробь 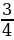 сократить нельзя, так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.
сократить нельзя, так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.
Дробь, числитель и знаменатель которой числа взаимно простые, называется несократимой.
5. Дробь 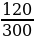 можно сразу сократить на наибольший общий делитель числителя и знаменателя, то есть на 60:
можно сразу сократить на наибольший общий делитель числителя и знаменателя, то есть на 60:
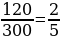 , но можно вести постепенно:
, но можно вести постепенно: 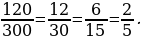
Дробь сокращают до тех пор, пока не получат в числителе и знаменателе взаимно простые числа.
6. Иногда удобно при сокращении дроби разложить числитель и знаменатель на несколько множителей, а потом уже сократить.
Например, 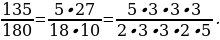
7. Сократим на 3 ・ 3 ・ 5 и получим 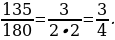 Дробь
Дробь 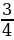 несократимая.
несократимая.
III. Работа по учебнику
1. Назовите несократимые дроби.
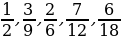
– Почему эти дроби являются несократимыми?
2. С. 58, № 5.331.
– Какая дробь получается в результате сокращения? (Несократимая.)
3. С. 58, № 5.334 (работа в паре).
– Дроби можно сокращать любым удобным способом.
Ответ:
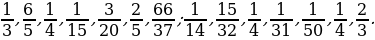
4. Какую часть составляет:
а) 20 от 80; б) 18 от 42; в) 12 от 60; г) 25 от 52?
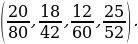
– Сократите получившиеся дроби.
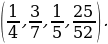
IV. Повторение изученного материала
1. С. 59, № 5.347.
Ответ: n = 15, c = 21, r = 1, z = 25, m = 4, c = 15.
2. С. 59, № 5.351. (24 км/ч.)
V. Работа над задачей
1. С. 59, № 5.341.
– Первый станок изготавливает 40 деталей за 12 часов, значит, его производительность составляет:
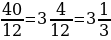 (детали).
(детали).
– Второй станок изготавливает 30 деталей за 9 часов, значит, его производительность составляет:
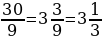 (детали).
(детали).
Таким образом, производительность обоих станков одинакова.
2. С. 59, № 5.342 (работа в паре).
– Что известно? Что неизвестно?
– Можно сразу ответить на вопрос задачи?
Ответ: 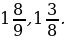
VI. Работа в рабочей тетради
С. 16, № 1, 2.
VII. Рефлексия
– Какая дробь называется несократимой?
– Приведите примеры несократимых дробей.
Домашнее задание
С. 60, № 5.357, 5.359, 5.360.







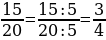 мы сможем разделить на одно и то же число, воспользовавшись основным свойством дроби. В дальнейшем это преобразование будем называть сокращением дроби.
мы сможем разделить на одно и то же число, воспользовавшись основным свойством дроби. В дальнейшем это преобразование будем называть сокращением дроби.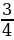 сократить нельзя, так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.
сократить нельзя, так как числа 3 и 4 – взаимно простые числа. Такую дробь называют несократимой.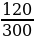 можно сразу сократить на наибольший общий делитель числителя и знаменателя, то есть на 60:
можно сразу сократить на наибольший общий делитель числителя и знаменателя, то есть на 60: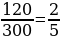 , но можно вести постепенно:
, но можно вести постепенно: 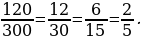
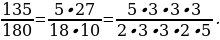
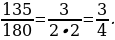 Дробь
Дробь 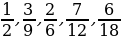
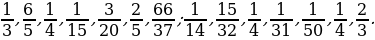
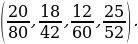
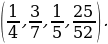
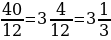 (детали).
(детали).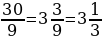 (детали).
(детали).