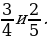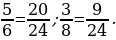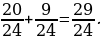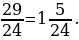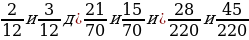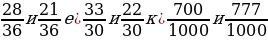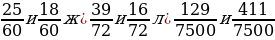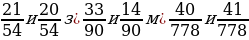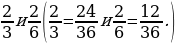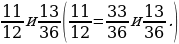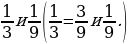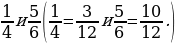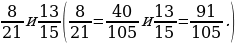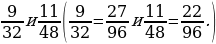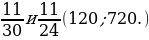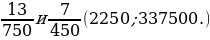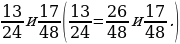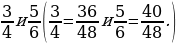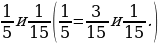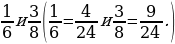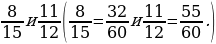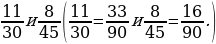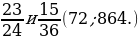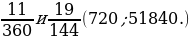У р о к № 2. Приведение дробей к общему знаменателю
Основная дидактическая цель урока: формировать умения приводить дроби к наименьшему общему знаменателю и находить дополнительный множитель в более сложных случаях; развивать логическое мышление.
Х о д у р о к а
I. Организационный момент
II. Устный счёт
1. Найдите наибольший общий делитель и наименьшее общее кратное чисел:
10 и 12; 12 и 8; 15 и 9; 6 и 4; 6 и 8; 12 и 15; 2 и 10; 16 и 20; 11 и 7.
Ответ:
10 и 12 (НОД – 2, НОК – 60.)
12 и 8 (НОД – 4, НОК – 24.)
15 и 9 (НОД – 3, НОК – 45.)
6 и 4 (НОД – 2, НОК – 12.)
6 и 8 (НОД – 2, НОК – 24.)
12 и 15 (НОД – 3, НОК – 60.)
2 и 10 (НОД – 2, НОК – 10.)
16 и 20 (НОД – 4, НОК – 80.)
11 и 7 (НОД – 1, НОК – 77.)
2. Насос наполняет бассейн за 48 мин. Какую часть бассейна насос наполнит за 1 мин?
3. С. 63, № 5.376 (устно).
(40, 0, 50, 18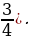
III. Работа по теме урока
Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю.
1. Найдите несколько общих знаменателей дробей.
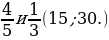
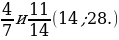

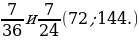
– Назовите их наименьший общий знаменатель. (15, 14, 72.)
Общим знаменателем дробей может быть любое общее кратное их знаменателей. При этом, как правило, стараются подобрать наименьший общий знаменатель (НОЗ) – тогда вычисления с дробями оказываются проще. Наименьший общий знаменатель равен наименьшему общему кратному знаменателей данных дробей.
2. Рассмотрим на примерах, как можно находить НОЗ дробей.
1) Приведём к общему знаменателю дроби 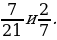
– В чём особенность чисел 21 и 7? (21 делится нацело на 7.)
Больший знаменатель – число 21 – делится на меньший знаменатель 7, следовательно, его можно взять в качестве общего знаменателя данных дробей. Этот общий знаменатель – наименьший из всех возможных.
Значит, нужно только дробь 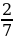 привести к знаменателю 21.
привести к знаменателю 21.
Для этого найдём дополнительный множитель: 21 : 7 = 3.
– Какой вывод можно сделать? (Если один знаменатель дроби делится на другой, то НОЗ будет больший знаменатель.)
2) Приведём к общему знаменателю дроби 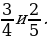
– Что вы можете сказать о числах 4 и 5? (Числа взаимно простые.)
Общий знаменатель данных дробей должен делиться и на 4, и на 5, т. е. быть их общим кратным. Общих кратных чисел 4 и 5 бесконечно много: 20, 40, 60, 80 и т. д. Наименьшее кратное – число 20 – произведение 4 и 5.
Значит, нужно привести каждую из дробей к знаменателю 20.
– Какой вывод можно сделать?
Если знаменатели дробей взаимно простые числа, то наименьшим общим знаменателем будет их произведение.
3. Сформулируйте правило приведения дробей к НОЗ.
(Учитель даёт задание найти НОЗ нескольких дробей.)
IV. Работа по учебнику
1. С. 62, № 5.364.
2. С. 62, № 5.369.
(12, 35, 90, 72.)
3. С. 63, № 5.373.
Ответ:
1) 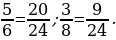
2) 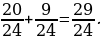
3) 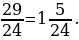
4. С. 62, № 5.370 (работа в паре).
Ответ:
а) 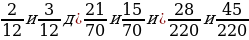
б) 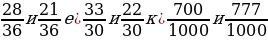
в) 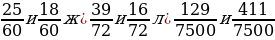
г) 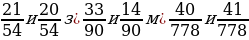
V. Повторение изученного материала
1. С. 63, № 5.380.
(5, 6, 6, 8.)
2. С. 64, № 5.386.
а) (2616 : 6 + 26 ・ 14) : 4 - 196 = (436 + 26 ・ 14) : 4 - 196 = (436 + 364) : 4 - 196 = 800: : 4 -196 = 200 - 196 = 4
б) (867 000 : 2125 - 396) ・ 25 = (408 - 396) ・ 25 = 12 ・ 25 = 300
в) 30 ・ 29 - 29 ・ 28 + 28 ・ 27 - 27 ・ 26 = (30 ・ 29 - 29 ・ 28) + (28 ・ 27 - 27 ・ 26) = 29 ・ (30 - 28) + 27 ・ (28 - 26) = 29 ・ 2 + 27 ・ 2 = 2 ・ (29 + 27) = 2 ・ 56 = 112
г) (392 + 39) + (402 - 40) = 39 ・ (39 + 1) + 40 ・ (40 - 1) = 39 ・ 40 + 40 ・ 39 = 2 ・ 40 ・ 39 = 80 ・ 39 = 3120
VI. Работа над задачей
С. 64, № 5.383.
Нуль не может быть первой цифрой. (5 вариантов.)
Вторая цифра – 0, 1, 4, 7, 8 или 9. (6 вариантов.)
Третья цифра – 0, 1, 4, 7, 8 или 9. (6 вариантов.)
Четвёртая цифра – 0, 1, 4, 7, 8 или 9. (6 вариантов.)
Пятая цифра – 0, 4 или 8. (3 варианта.)
5 ・ 6 ・ 6 ・ 6 ・ 3 = 3240 пятизначных чисел.
VII. Работа в рабочей тетради
С. 18, № 3, 5.
VIII. Самостоятельная работа
В а р и а н т 1
1. Приведите дроби к общему знаменателю 36.
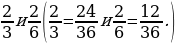
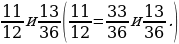
2. Приведите дроби к наименьшему общему знаменателю.
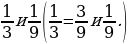
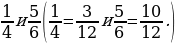
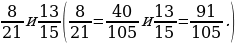
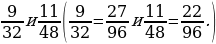
3. Приведите дроби к общему знаменателю.
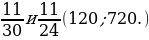
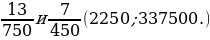
В а р и а н т 2
1. Приведите дроби к общему знаменателю 48.
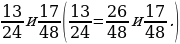
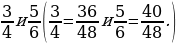
2. Приведите дроби к наименьшему общему знаменателю.
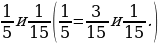
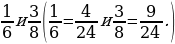
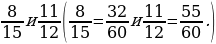
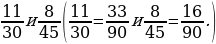
3. Приведите дроби к общему знаменателю.
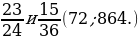
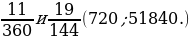
IX. Рефлексия
– Как привести дроби к наименьшему общему знаменателю?
– На каком свойстве основано правило приведения дробей к общему знаменателю?
– Как найти общий знаменатель данных дробей?
– Как найти дополнительный множитель для каждой дроби?
Домашнее задание
С. 64, № 5.388, 5.390.







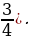
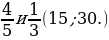
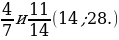

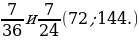
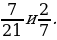
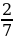 привести к знаменателю 21.
привести к знаменателю 21.