Разработка урока

М(5) Дата: 26.11.2024

У р о к № 57 Тема: « Дробь. Правильные и неправильные дроби»

Образовательная цель: организация деятельности учащихся по осмыслению понятия обыкновенная дробь, правильная и неправильная дробь закреплению умения распознавать математические объекты в реальных жизненных ситуациях.

Развивающая цель: развитие логики, памяти , внимания.

Воспитательная цель: точность, аккуратность математической записи.

Планируемые результаты:

-личностные

1. Формирование устойчивого познавательного интереса

2. Развитие коммуникативной компетенции при общении и сотрудничестве

3. Формирование у учащихся ответственного отношения к учению, готовности и способности к саморазвитию на основе мотивации к обучению и познанию

- метапредметные результаты:

1. Освоение способности представлять результаты решения заданий на дроби

Тип урока. Урок сообщения новых знаний

Метод. Словесный, беседа, рассказ.

Литература /основная/ Н. Я, Виленкин и др. Математика 5 класс, часть 1

Дополнительная литература: ФГОС в помощь школьному учителю. Автор И. А, Чердаклиева . Поурочные разработки по математике к УМК Н. Я. Виленкин и др., 5 класс .

Обязательная литература:

1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.

Ход урока

Организационный момент .

проверка посещаемости;

проверка готовности к уроку;

проверка дз №№ 731,732.

Актуализация знаний.

• Устный счёт

• числитель и знаменатель обыкновенной дроби;

• правильная, неправильная дробь.

Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы.

Правильные дроби – это дроби, в которых числитель меньше знаменателя

Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя.

Мотивация учебной деятельности. Часто в жизни мы слышим такие выражения: «Прошел половину пути», «Купил четвертинку хлеба», «Занял полтинник» , «Сделал третью часть от работы». Все эти выражения связаны с новым понятием «дробь». О ней сегодня и пойдёт речь.

Сообщение нового материала.

Чтобы ввести понятие дроби, выполним следующее задание на реальных примерах из жизни пояснить доли, части , дроби. Разрез ленты или торта ,расфасовка продуктов, разбиение килограмма.

Две части будут весить две третьих килограмма.

Если на отрезке АС укладывается ровно 3 раза отрезок длиной одна пятая сантиметра, то говорят, что длина отрезка равна три пятых сантиметра.

Такие записи называются обыкновенными дробями или просто дробями.

Дробь показывает какую-то часть от целого или единицы. Например, дробь семь восьмых показывает семь восьмых части от единицы.

Любую дробь можно записать в виде буквенного выражения: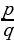

Обозначенное таким образом число называют рациональным числом. При этом p называется числителем дроби (он всегда находится над чертой), а q – знаменателем дроби (он всегда находится под чертой).

Рассмотрим виды обыкновенных дробей. Обыкновенные дроби можно разделить на следующие виды – правильные, когда числитель меньше знаменателя, и неправильные, когда числитель равен или больше знаменателя.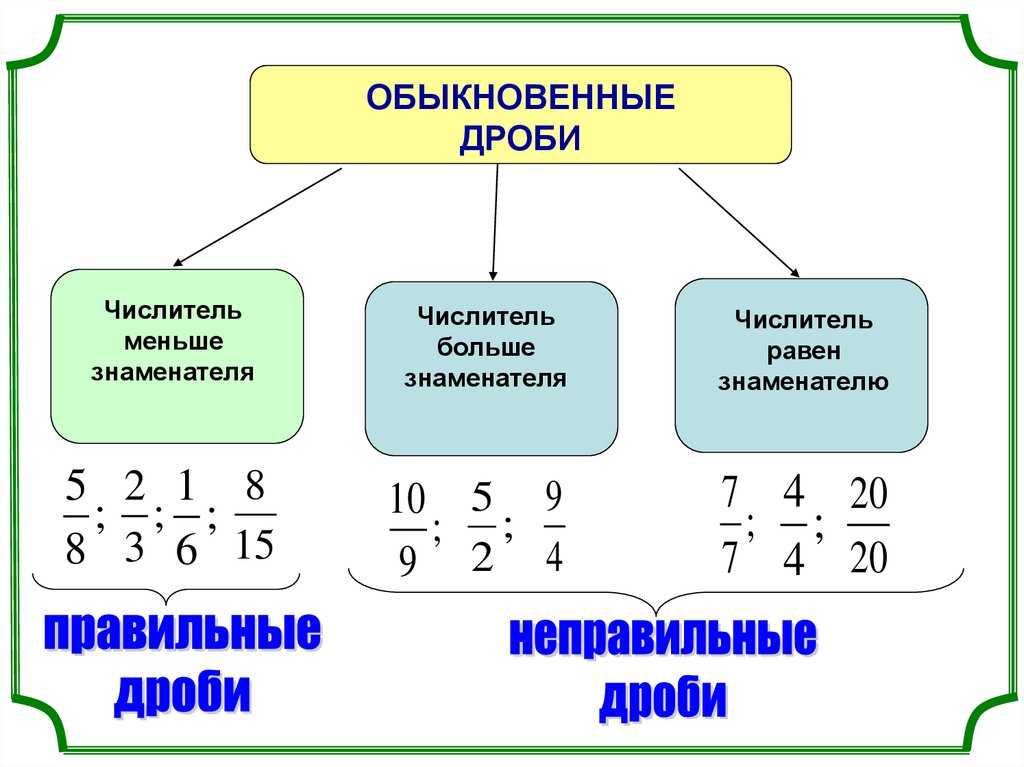

Сколько часов содержится в четверти суток? Так как в сутках 24 часа, то нам по условию надо найти четвёртую часть, т. е. разделить двадцать четыре часа на четыре части. Решим задачу, используя понятие обыкновенной дроби.

В коробке находилось два вида конфет: 5 шоколадных и 6 карамелек. Какую часть всех конфет занимают карамель и шоколад?

Решение: для начала найдём общее количество конфет в коробке, для этого сложим все виды конфет.

5 + 6 = 11 – конфет в коробке.

Теперь можно найти, какую часть от общего количества конфет занимает карамель, а какую шоколадные конфеты. Для этого запишем результат в виде обыкновенной дроби, где в знаменателе укажем общее число конфет. Пять одиннадцатых – часть шоколадных конфет, а шесть одиннадцатых – часть карамели.

Закрепление

№ 1. Сколько минут содержится в одной трети часа?

Решение: для решения этой задачи достаточно вспомнить, что 1 ч = 60 мин.

Найдём третью часть от 60 минут, для этого:

60 мин : 3 = 20 мин. Ответ: 20 мин.

№ 2. Длина отрезка АВ равна 10 см. Чему равен отрезок, длина которого составляет две пятых от длины отрезка АВ?

Решение: сначала найдём, чему равна одна часть из 5 отрезков.10 см : 5 = 2 см – одна часть.

По условию задачи нужно найти 2 части из пяти, поэтому: 2 см · 2 = 4 см

Ответ: 4 см.

Подведение итогов урока.

Домашнее задание: