| Технологическая карта урока |
|
Предмет | Геометрия |
| Класс
| 11 |
| Дата | 15.11.22 |
| УМК (название учебника, автор, год издания) | Геометрия, 10-11: Учеб. для общеобразоват. Учреждений/ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2013. |
| Тема урока
| Вычисление углов между прямыми и плоскостями. |
| Цель урока | повторить с обучающимися вопросы теории, касающейся скалярного произведения векторов; формировать умения вычислять скалярное произведение векторов, показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, а также между прямой и плоскостью. |
| Задачи урока | Показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, а также между прямой и плоскостью. Формирование мировоззрения: показать, что источник возникновения изучаемых понятий представляет собой определённую систему знаний в геометрии. |
| Планируемые результаты |
|
| предметные | метапредметные
| личностные |
| Обучающиеся должны овладеть приёмами и навыками решения задач на вычисление углов в пространстве, научиться применять изученный теоретический материал на практике, при этом достаточно хорошо должна быть развита самостоятельность при решении задач разными методами.
| Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений. Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций. Познавательные: осуществлять сравнение и классификацию по заданным критериям | Формирование устойчивой мотивации к проблемно-поисковой деятельности |
| Техническое обеспечение урока
| Компьютер, мультимедийный проектор |
| Дополнительные методическое и дидактическое обеспечение урока | Геометрия: Учебник для 10-11 кл. ср. шк./ Л.С. Атанасян – М.: Просвещение, 2001;карточки с заданиями на печатной основе.
|
Содержание урока
-
ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
-
АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ.
-
Устные упражнения.
-
Дано 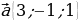 ,
, 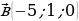
Найти косинус угла между векторами 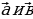 , определить вид угла.
, определить вид угла.
(ответ cos 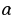 =
=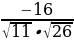 угол между векторами тупой)
угол между векторами тупой)
-
Дано 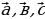
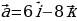
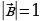
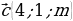
Угол между векторами 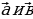 равен
равен 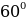
Найти 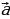 ∙
∙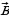
m, при котором вектора 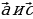 перпендикулярны
перпендикулярны
(ответ 5;3)
-
Устный опрос.
Повторяем теоретический материал. Фронтально работаем с классом.
- Как находят координаты вектора, если известны координаты его начала и конца?
-Как находят координаты середины отрезка?
-Как находят длину вектора?
-Как находят расстояние между точками?
-Как вы понимаете выражение «угол между векторами»?
-Что называется скалярным произведением векторов?
-Чему равно скалярное произведение перпендикулярных векторов?
-Чему равен скалярный квадрат вектора?
-Свойства скалярного произведения?
-Формула для нахождения косинуса угла между векторами из определения скалярного произведения векторов и через координаты векторов?(слайд 2,3)
-
ЗАДАЧИ ЕГЭ (базовый)
№ 27054 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
27078  Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
№ 245359  Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
-
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.
Для вычисления угла между двумя прямыми удобно использовать скалярное произведение. Прежде рассмотреть задачи на вычисление углов введем понятие направляющего вектора.
Направляющим вектором прямой называется ненулевой вектор, лежащий на прямой или на прямой параллельной данной.
Рассмотреть задачи 1 и 2, на нахождение угла между прямыми, между прямой и плоскостью. Можно класс разделить на две группы и предложить обучающимся разобрать решение самостоятельно. Затем более подготовленные учащиеся представляют решение данных задач на доске.
Задача 1. Найти угол между двумя прямыми, если известны координаты направляющих векторов этих прямых.(слайд 4)
Пусть даны две прямые a и b, и их направляющие вектора 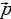 и
и 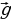 , заданные координатами,
, заданные координатами, 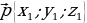 и
и 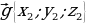 . Найдем угол β между прямыми.
. Найдем угол β между прямыми.
Возможны два случая:
-
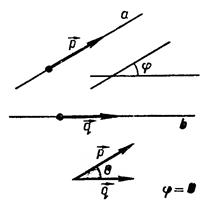
Если угол φ между векторами острый, то угол φ равен углу β между прямыми. Тогда по формуле скалярного произведения векторов: Cos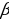 =
=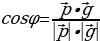
(см. рис. 1).
Рис. 1. Острый угол между прямыми.
-
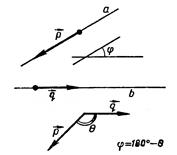
Если угол φ между векторами тупой, то угол между прямыми равен (180-φ),то есть
Cos =
=
(см. рис. 2).
Рис.2. Тупой угол между прямыми
Можно объединить два случая в одной формуле: Cos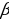 =
=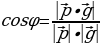 , где
, где 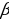 – угол между прямыми, а вектора
– угол между прямыми, а вектора 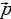 и
и 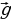 , - их направляющие вектора.
, - их направляющие вектора.
Используя формулы для нахождения угла между векторами в координатах, можно записать cos 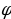 =
=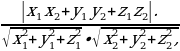
Задача 2. Найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости.(слайд 5)
Напомним, что углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.
Пусть даны направляющий вектор 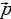 для прямой а и ненулевой вектор
для прямой а и ненулевой вектор 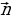 , перпендикулярный к плоскости
, перпендикулярный к плоскости 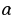 , заданные координатами,
, заданные координатами, 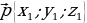 и
и 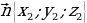 . Если нам известен направляющий вектор
. Если нам известен направляющий вектор 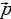 прямой a и вектор
прямой a и вектор 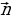 , перпендикулярный плоскости α (см. рис. 3), то мы можем выразить угол между прямой и плоскостью через угол между данной прямой и прямой, перпендикулярной плоскости α
, перпендикулярный плоскости α (см. рис. 3), то мы можем выразить угол между прямой и плоскостью через угол между данной прямой и прямой, перпендикулярной плоскости α
sin 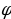 =cos(
=cos(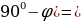 Cos
Cos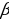 =
=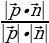
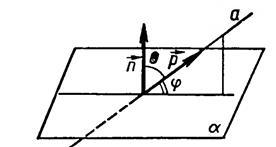
Рис. 3. Угол между прямой и плоскостью
-
ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО.
Задача 1. (ЕГЭ)
Дан прямоугольный параллелепипед АВСД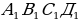 , ребра которого соответственно равны ДА=1, ДС=2, Д
, ребра которого соответственно равны ДА=1, ДС=2, Д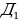 = 3. Найти угол между прямыми С
= 3. Найти угол между прямыми С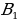 и
и 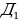 В.
В.
Наметить ход решения задачи совместно, в результате фронтального опроса, затем один учащийся работает у доски, остальные в тетрадях.(слайд 6)
Ход решения задачи:
1.Ввести прямоугольную систему координат с центром в точке Д, определить координаты точек С,В, 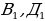 .
.
2.Расмотрим направляющие вектора для прямых С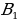 и
и 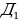 В, найти их координаты.
В, найти их координаты.
3.По формуле найти косинус угла между направляющими векторами.
(ответ 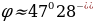 )
)
Задача 2. №464(а)
Работу по решению данной задачи провести в парах, предварительно составив вновь ход решения, фронтально работая с классом. При необходимости учитель оказывает индивидуальную консультацию, проверку провести с помощью слайда 7.
(ответ 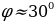 )
)
Задача 3. № 467(а)
Класс разделить на две группы. Решение провести двумя способами координатно-векторным методом, рассмотренным на уроке. Обычным способом, используя теорему косинусов, понятие угла между скрещивающимися прямыми, теорему Пифагора.
Обучающиеся работают в группах самостоятельно, при необходимости учитель консультирует, оказывает помощь. Затем решение каждой группы представляется на доске, проверяется и дополняется.(слайд 8,9)
№ 467(а). В прямоугольном параллелепипеде АВСД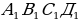 , АВ=ВС=
, АВ=ВС=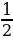 А
А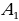 . Найти угол между ВД и С
. Найти угол между ВД и С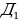 .
.
Решение
Первый способ: 1. Введем систему координат с центром в точке В.
2. Пусть единица измерения отрезков выбрана так, что А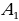 =2, тогда АВ=ВС=1.
=2, тогда АВ=ВС=1.
3.Определим координаты точек В(0;0;0), Д(1;1;0), С(1;0;0), 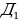 (1;1;2)
(1;1;2)
4.Определим координаты направляющих векторов прямых ВД и С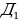 ,
, 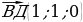 ,
, 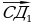
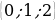
5.Используя векторы 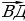 и
и 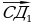 , находим косинус угла
, находим косинус угла 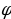 между прямыми ВД и
между прямыми ВД и  .
.
6.cos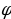 =
=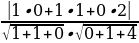 =
=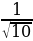
7.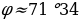
Второй способ: 1. Угол между скрещивающимися прямыми ВД и С равен углу между прямыми ВД и В
равен углу между прямыми ВД и В , так как С
, так как С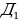 параллельно В
параллельно В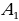 , по определению угла между скрещивающимися прямыми.
, по определению угла между скрещивающимися прямыми.
2. В треугольнике ВД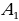 по теореме Пифагора находим В
по теореме Пифагора находим В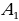 =
=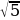 ,
,
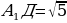 , ВД =
, ВД =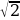
3. По теореме косинусов получим 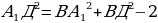 В
В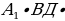 cos
cos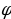 , а тогда cos
, а тогда cos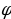 =
=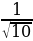 , то есть
, то есть 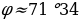
Ответ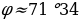
-
САМОСТОЯТЕЛЬНАЯ РАБОТА
Решить самостоятельно по вариантам
Уровень А --- № 464(б,в).
Уровень В --- №467 (б)- координатным методом
Решение оформляется в тетрадях и сдается учителю на проверку.
-
ПОСТАНОВКА ДОМАШНЕГО ЗАДАНИЯ
Обучающимся следует прочитать дома п.52, № 464 (г), № 444 (4), №467 (б)- кто не выполнил в самостоятельной работе (двумя способами), кто выполнил методом координат, вторым способом.
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА
Какие понятия были введены на уроке? Как определить между прямыми? Какие вектора называются направляющими для прямой? Как определить угол между прямой и плоскостью? На чем основан вывод этих формул? В чем ход решения геометрической задачи координатным методом для нахождения углов между прямыми?
Итак, на примере решения сегодняшних задач мы убедились, что использование координатно-векторного метода значительно облегчает решение некоторых задач. А
наш урок я хочу закончить словами: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию» - Ян-Амос Каменский.






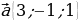 ,
, 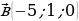
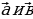 , определить вид угла.
, определить вид угла.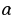 =
=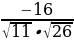 угол между векторами тупой)
угол между векторами тупой)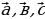
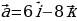
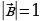
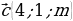
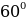
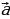 ∙
∙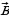
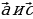 перпендикулярны
перпендикулярны Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.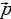 и
и 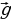 , заданные координатами,
, заданные координатами, 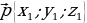 и
и 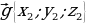 . Найдем угол β между прямыми.
. Найдем угол β между прямыми.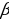 =
=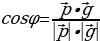

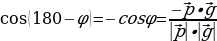

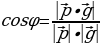 , где
, где 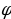 =
=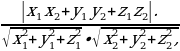
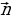 , перпендикулярный к плоскости
, перпендикулярный к плоскости 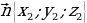 . Если нам известен направляющий вектор
. Если нам известен направляющий вектор 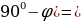 Cos
Cos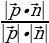

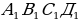 , ребра которого соответственно равны ДА=1, ДС=2, Д
, ребра которого соответственно равны ДА=1, ДС=2, Д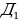 = 3. Найти угол между прямыми С
= 3. Найти угол между прямыми С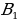 и
и 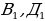 .
.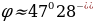 )
)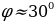 )
)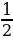 А
А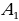 . Найти угол между ВД и С
. Найти угол между ВД и С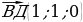 ,
, 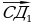
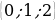
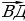 и
и 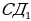 .
.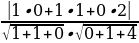 =
=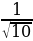
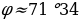
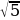 ,
,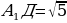 , ВД =
, ВД =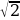
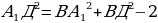 В
В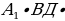 cos
cos

















