УРОК МАТЕМАТИКИ В 8 КЛАССЕ «Средняя линия трапеции»
Тип урока: урок «открытия» нового знания.
Цели урока:
Образовательные:
Формирование понятия средней линии трапеции;
изучение свойств средней линии трапеции;
формирование умения применять знания о средней линии трапеции при решении задач.
Развивающие:
развивать у обучающихся логическое мышление при решении геометрических задач, интерес к предмету, познавательную и творческую активность, математическую речь, память, внимание;
учить самостоятельно добывать знания.
Воспитательные:
воспитывать у учащихся ответственное отношение к учебному труду, волю;
формировать эмоциональную культуру и культуру общения.
Методы обучения: словесный, наглядный, деятельностный.
Формы обучения: коллективная, индивидуальная, парная.
Оборудование: мультимедиа проектор, экран, шаблоны трапеций, тексты самостоятельной работы в двух вариантах, плакаты с чертежами, у каждого ученика набор разноцветных трапеций.
Структура урока:
I.Мотивация (самоопределение) к учебной деятельности.
II. Актуализация и пробное учебное действие
III. Выявление места и причины затруднения
IV. Целеполагание и построение проекта выхода из затруднения
V. Реализация построенного проекта
VI. Первичное закрепление новых знаний
VII. Самостоятельная работа с самопроверкой
VIII. Включение в систему знаний и повторение
IX.Рефлексия
Ход урока
Мотивация (самоопределение) к учебной деятельности.
(слайд № 1 )
- Аристотель сказал: «Математика выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного».
II. Актуализация и пробное учебное действие
- На предыдущих уроках вы познакомились с понятием средней линии треугольника, свойствами средней линии треугольника. (слайд №2)
- Сформулируйте определение средней линии треугольника.
- Сформулируйте свойства средней линии треугольника.
- Сколько существует средних линий в треугольнике?
- А теперь давайте вспомним, какая фигура называется трапецией? (слайд №3). Назовите основания и боковые стороны трапеции.
- Ребята, как вы думаете, есть ли в трапеции средняя линия, похожая на среднюю линию треугольника?
(Заслушать ответы детей)
III. Выявление места и причины затруднения
- Вы можете дать определение средней линии трапеции? (Нет)
- Почему? (Не изучали)
- А свойства средней линии трапеции можете назвать? (Нет)
- Да, ответов на эти вопросы вы пока не знаете, т.е. вы столкнулись с затруднением, возникла проблема, которую нам необходимо решить.
IV.Целеполагание и построение проекта выхода из затруднения
-Так о чем же мы с вами будем говорить на уроке? (О средней линии трапеции)
- Значит тема нашего урока…( Средняя линия трапеции) (слайд №4)
- Давайте попробуем сформулировать цели урока.
- Что мы хотим узнать о средней линии трапеции? (Что называется средней линией трапеции, какими свойствами она обладает)
Цели урока: сформулировать определение средней линии трапеции, сформулировать и доказать свойства средней линии трапеции, учиться применять их при решении задач (слайд № 5).
-Откройте тетради и запишите число и тему урока: «Средняя линия трапеции»
- Учитывая цели урока, давайте составим план выхода из затруднения: (слайд №6)
1) Выяснить, что может называться средней линией трапеции;
2) Сформулировать предполагаемые свойства средней линии трапеции;
3) Доказать свойства средней линии трапеции.
V. Реализация построенного проекта
- Давайте попытаемся сформулировать определение средней линии трапеции аналогично определению средней линии треугольника.
Наводящие вопросы:
- Какие точки соединяет средняя линия треугольника? Сколько середин сторон у трапеции? (4) Как их можно соединить? Какие это варианты соединений? (боковая сторона - боковая сторона, боковая сторона – основание, основание – основание)
На доске:
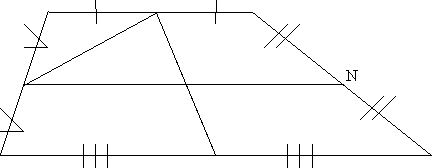
- Какой из этих отрезков называется средней линией трапеции. Почему? (Это отрезок МN, соединяющий середины боковых сторон трапеции. Так как только этот отрезок, мы замечаем, может быть параллелен основаниям трапеции, точно так же, как средняя линия треугольника параллельна третьей стороне треугольника)
- Сформулируйте определение средней линии трапеции с опорой на выше изложенное.
Откройте учебник на странице 75,п.59, давайте прочитаем определение средней линии трапеции.
- Определение, сформулированное вами, совпадает с определением учебника? (Да) Первый пункт плана выполнен.
Сколько средних линий можно провести в трапеции? (Ответ: 1)
-Начертите в тетрадях трапецию ABCD, проведите ее среднюю линию MN.
- Какие точки соединяет средняя линия трапеции?
Запишите в тетрадях:
AM=MB, CN=ND =› MN – средняя линия трапеции (на доске и в тетрадях)
- Вернемся к нашему плану? Какой следующий пункт?
- Какое первое свойство вы уже заметили? (Средняя линия трапеции параллельна основаниям) Но это пока только предположение, его еще необходимо доказать.
-Запишем наше предположение:
1) MN║BC║AD (на доске и в тетрадях)
-Может быть средняя линия трапеции обладает еще каким-нибудь свойством? Давайте проведем эксперимент. Работать будем в парах.
-У вас на столах лежат конверты, возьмите конверт№1 и достаньте из него шаблон трапеции и таблицу. Измерьте основания и среднюю линию трапеции, запишите полученные данные в таблицу. (На каждом ряду – свой шаблон).
| Меньшее основание BC |
|
| Большее основание AD |
|
| Средняя линия MN |
|
Теперь внесем полученные данные каждого ряда в общую таблицу. (слайд№7)

- Давайте попробуем установить зависимость между средней линией и основаниями трапеции.
Наводящий вопрос: сравните сумму оснований и среднюю линию.
- Чему равна средняя линия трапеции?
(Средняя линия трапеции равна полусумме оснований трапеции).
2) MN = ½(BC + AD) (на доске и в тетрадях)
Откройте учебник на странице 75,п.59, найдите теорему 6.8, давайте прочитаем теорему о свойствах средней линии трапеции. (слайд№8)
Т.е. ваши предположения о свойствах средней линии трапеции действительно верны.
Но, как сказал известный советский математик Хинчин А.Я.,
« В математической науке все, что не обосновано до конца, расценивается как абсолютно необоснованное» и эту теорему, как и любую другую, надо доказать.
Доказательство этой теоремы подготовила Рита Анякова. Давайте послушаем ее. (Теорему о свойствах средней линии трапеции доказывает ученица у доски)
- Все пункты плана мы с вами выполнили, а теперь немного отдохнем.
Физкультминутка
VI. Первичное закрепление новых знаний
- А сейчас потренируемся решать задачи на применение определения и свойств средней линии трапеции.
- Решение задач по готовым чертежам (2 задачи)
(слайды № 9, 10)
- Молодцы, с задачами вы справились.
VII.Самостоятельная работа с самопроверкой
- А теперь выполним самостоятельную работу по вариантам. Из конверта №3 достаньте тексты самостоятельной работы.
1-е задание с выбором ответа. Внимательно прочитайте все варианты ответов и обведите номер правильного ответа. (правильных ответов может быть 1 или 2)
Задания 2,3. Это задачи, аналогичные тем, что мы решали. Запишите кратко необходимые вычисления и ответ.
Самопроверка (ответы выведены на экран)
- Рядом с правильными ответами поставьте «+», с неправильными «–»
- Поднимите руку те, у кого все ответы правильные.
- Кто допустил одну ошибку?
- Остальные могут взять свои работы домой, чтобы найти свои ошибки и исправить их.
VIII. Включение в систему знаний и повторение
Решить задачу №3 (слайд №12)
IX.Рефлексия
Постановка домашнего задания (cлайд № )
п.59, № 60, № 69, № 66* (для желающих) – стр.83-84
Вопросы 1 7-19 (стр.79)
- А теперь давайте подведем итог урока.
- С каким новым понятием вы сегодня познакомились?
- Сформулируйте определение средней линии трапеции.
- Перечислите свойства средней линии трапеции.
- Достигли мы целей, поставленных в начале урока?
- А сейчас давайте оценим свою работу на уроке.
- Возьмите конверт №4, достаньте трапеции.
- Кому сегодня на уроке все было понятно, кто полностью справился со всеми заданиями, поднимите зеленую трапецию.
- Те, кто понял тему, но в решении задач допустил 1-2 ошибки, поднимите желтую трапецию.
- Кто не до конца понял тему и были ошибки в задачах, поднимите красную трапецию.
-Не огорчайтесь, что сегодня у вас не все получилось, на последующих уроках вы закрепите полученные знания.
- Все вы хорошо поработали, поставленных целей достигли. Спасибо всем за сотрудничество!

















