Россия, Феодосия
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 11.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 13.05.2025 14:22
Крищенко Татьяна Владимировна
учитель математики
886
64 257 
Местоположение
Специализация
Разработка урока по алгебре на тему: "Свойства числовых неравенств", 8 класс.
Категория:
Алгебра
06.09.2024 11:40
Просмотр содержимого документа
«Разработка урока по алгебре на тему: "Свойства числовых неравенств", 8 класс.»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«Школа №19 им С.Н. Котова г.Феодосии Республики Крым»
Разработка урока
по алгебре, 8 класс (линия УМК Мерзляка А.Г.)
на тему: «Свойства числовых неравенств»
Урок разработала
Крищенко Татьяна Владимировна,
учитель математики
г.Феодосия, 2022г.
Дата: _________ Класс: 8-А, 8-Б
Тема урока: "Свойства числовых неравенств" (слайд 1)
Цель:
рассмотреть теоремы о почленном сложении и умножении числовых неравенств; сформировать навыки применения их к решению простейших задач на оценку выражений; закрепить свойства неравенств; привитие интереса к изучаемому предмету; формирование математического мышления и умения учащихся воспроизводить мысли устной и письменной речью.
Планируемые образовательные результаты
Личностные: развивать находчивость при решении задач. Критически оценивать полученный ответ, осуществлять самоконтроль. Готовность учиться самостоятельно. Доброжелательно и уважительно относиться к другим людям, уметь работать в режиме диалога.
Метапредметные:
Принимать учебную проблемную ситуацию и рассматривать ее как начальный этап ее последующего обсуждения и разрешения. Выдвигать гипотезы и их обосновывать. Использовать знаково-словесные способы кодирования информации. Структурировать знания. Осознанно строить речевое высказывание в устной форме.
Предметные: Уметь читать числовые неравенства; знать свойства числовых, уметь доказывать их и применять их на практике. Уметь оценивать значение выражения, используя свойства числовых неравенств.
Планируемые результаты: Учащийся научится применять полученные знания при решении практических задач, оперировать терминами, закрепят свойства неравенств.
Тип урока: урок изучения и первичного закрепления новых знаний
План урока:
-
Организационный этап;
-
Проверка д.з.
-
Актуализация опорных знаний и умений учащихся (повторение ранее пройденного материала);
-
Создание проблемной ситуации и поиск путей решения проблемы
-
Формулировка целей урока
-
Формирование новых знаний;
-
Разминка для глаз
-
Применение теоретических положений в условиях выполнения упражнений. Формирование и отработка навыков и умений, изученных в ходе урока;
-
Самостоятельное использование сформированных умений и навыков Самостоятельная работа
-
Домашнее задание
-
Итоги урока.
-
Рефлексия деятельности
ХОД УРОКА
1.Организационный момент (слайд № 2 )
Сообщить девиз урока: «Слушай, что говорят;
говори, что знаешь;
делай, что должен;
будет, что нужно.»
С.Ковалевская.
2. Проверка домащнего задания (слайд № 3)
Решение показывается с помощью проектора и компьютера.
№ 758 (б,г)
Зная, что 5
Ответ: б) - 50
№ 761 (а) Оцените периметр квадрата со стороной a см, если 5,1 ≤ а ≤ 5,2
Как найти периметр квадрата. Ответ: 20,4 ≤ а ≤ 20,8
3. Актуализация опорных знаний и умений учащихся (повторение ранее пройденного материала)
(слайд № 4) Устная работа: Сформулируйте теоремы, выражающие основные свойства числовых неравенств.
Устно (условия заданий проектируются на экране, работа проходит фронтально, при выполнении заданий учащиеся поясняют, какие теоремы применяли, т.е., что можно делать с обеими частями неравенства)
- Теоремы, выражающие основные свойства числовых неравенств.
(слайд № 5) Теорема 1. Если аb, то b b , то b а
Теорема 2. Если аb и b
Теорема 3. Если a
(Если к обеим частям верного неравенства прибавить одно и тоже число, то получится верное неравенство)
(слайд № 6) Теорема 4(1). Если обе части верного неравенства умножить или разделить на одно и тоже положительное число, то получится верное неравенство
(слайд № 7)Теорема 4(2). Если обе части верного неравенства умножить или разделить на одно и тоже отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
(слайд № 8) Следствие из теоремы: если а и b – положительные числа
и a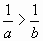 
. 2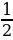 
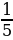
Повторим на конкретных примерах, как действуют эти правила.
(слайд № 9) 1.Найди ошибку ( устно) ( если неверно поднимаете руку вверх)
Пусть x y, выберите верные неравенства:
-
x – 3
-
5x 5 y
-
8 + x y + 8
-
−7x −7y
-
10 – x
(слайд № 10) 2.Блиц-опрос (устно) . Пусть a или , чтобы получилось верное неравенство?
1) a + 4 b + 4
2) −3,2a −3,2b
3) 10,5a 10,5b
4) b – 6 a – 6
5) 3 b 3 a
(слайд № 11) 3(устно)Запишите верное неравенство, которое получится, если:
а) К обеим частям неравенства 3 -2 прибавить число 5;
б) Из обеих частей неравенства -4
в) Обе части неравенства 5-1 умножить на -2;
г) Обе части неравенства 9
(слайд № 12) 4. (письменно) Оцените значение выражений и заполните пропуски, напишите знаки сравнения.
Если 7 x , то 4x, – 3 + x, – x, 1/x
4* 7 x ; 28 x
7-3 x x 8
-7 -x -11; -11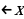 
; 
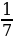
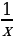
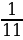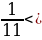
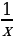
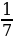
4.Создание проблемной ситуации и поиск путей решения проблемы ( мотивация учащихся к изучению новой темы)
Часто значения величин, являющихся результатами измерений, не точны. Измерительные приборы, как правило, позволяют лишь установить границы, между которыми находится точное значение.
Предложить обучающимся задачу
(слайд № 13 ) «Измеряя длину а и ширину b прямоугольного участка, (в метрах), нашли
что 23 a b 10. Оцените длину изгороди вокруг этого участка и его площадь».
Возможные наводящие вопросы :
-
Как найти периметр и площадь прямоугольника.
-
Что нужно сделать, чтобы оценить площадь и периметр?
-
Достаточно ли знания изученных ранее свойств для решения задачи?
Дети: Читают задачу, анализируют. Выдвигают свои способы (гипотезы) для решения поставленной задачи. Отвечают на вопросы :
-
Р=2*(а+b)
S=a*b.
-
Для оценки периметра нужно почленно сложить неравенства, а затем все части неравенства умножить на 2.
Для оценки площади необходимо умножить неравенства почленно.
Не знаем свойств когда неравенства почленно перемножаются и складываются
5.Формулировка темы урока. (слайд № 14 )
Формулировка целей урока. (слайд № 15 )
6. Изучение нового материала
Теперь давайте рассмотрим теоремы о почленном сложении и умножении числовых неравенств.
Теорема 5. (слайд № 16 )
Если a b и c d, то a + c b + d
Доказательство
Прибавим к обеим частям неравенства a b число c, получим a + c b + c
Прибавим к обеим частям неравенства c d число b, получим b + c b + d
Из неравенств a + c b + c и b + c b + d следует, что a + c b + d.
Вывод: Если почленно сложить верные неравенства одного знака, то получится верное неравенство.
Пример 1. Сложите числовые неравенства:
Например: -7-13
+ 7 + 7 2
0 -11 верно
Теорема 6. (слайд № 17 )
Если a b и c d, где a, b, c, d – положительные числа, то aс bd.
Доказательство
Умножим обе части неравенства a b на положительное число c, получим aс bd.
Умножим обе части неравенства cd на положительное число b, получим bс bd.
Из неравенств ac bc и bc, следует, что aс bd
Вывод: Если перемножить почленно верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.
Пример 2. Перемножьте числовые неравенства:
Например: (слайд № 18 )
76 -3
* 3 * 7 2 – 4
2112 верно 12
Следствие. : (слайд № 19)
Если числа а и b положительные и а b, то an bn ( n– натуральное число)
Например: 3 2, значит 33 23
27 8 верно
Заметим, что все рассмотренные свойства неравенств справедливы и в случае нестрогих неравенств:
если a b и c d, то a + c b + d;
если a b, c d и a, b, c, d – положительные числа, то ac bd;
если a b и a, b – положительные числа, то , где n – натуральное число.
Учащиеся решают (устно)
Задания из дидактического материала:
1. Сложите почленно неравенства: (слайд № 20 )
-5-25 и -2 -5 7833 и -22-23 32-1 и 147
2. Перемножьте почленно неравенства: (слайд №21)
55 и 43 53,5 и 62 21 и 43
Возвращаемся к проблемной задаче.
Решают задачу №2. (слайд № 22)
Обучающиеся решают задачу.
23 м a
9 м b 10 м
32 мa+b
64 м P
Тогда с помощью теоремы 6 можно оценить площадь прямоугольника. Имеем:
23*9м2 abм2
207 м2 S м2
Вообще, если известны значения границ величин, то, используя свойства числовых неравенств, можно найти границы значения выражения, содержащего эти величины, т. е. оценить его значение.
Разминка (для глаз) (слайд № 23)
- Не поворачивая головы, обведите взглядом стену класса по периметру по часовой стрелке, классную доску по периметру против часовой стрелки, прямоугольник, изображенный на слайде по часовой стрелке(красной) и следующий против часовой стрелки. Пробегите взглядом по жёлтой линии , затем по голубой. Поверните голову налево и посмотрите на линию горизонта, а теперь на кончик своего носа. Закройте глаза, сосчитайте до 5, откройте глаза и продолжим работу
6. Закрепление изученного материала
1.Решает учитель (слайд № 24)
Пример: Зная, что 7≤ x ≤9
2 ≤ y ≤ 5 Оцените: x+y , x-y , xy ,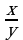 
Решение: 7 ≤ x ≤ 9 7 ≤ x ≤ 9
+ 2 ≤ y ≤ 5 -5 ≤ -y ≤ -2
9 ≤х+у≤14 2≤ x-y ≤ 7
7≤ x ≤9 7≤x≤9
*2 ≤ y ≤ 5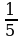 
≤
≤
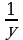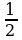
14≤xy≤45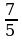 
≤ ≤
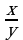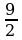
№ 768. Выполняют учащиеся
Выполним а), в), затем б), г) (слайд № 25 )
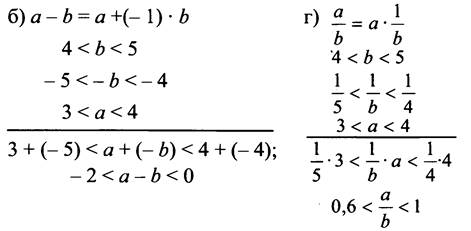
7. Самостоятельная работа (с выставлением оценки)
Организация и контроль за процессом решения задач. Организация самоконтроля по готовому решению
Самостоятельно работают над заданиями. (слайд № 26 )
Проверяют себя по шаблону (слайд № 27 )
8. Итоги урока (слайд №28 )
-
Сформулируйте теорему о почленном сложении числовых неравенств.
-
Сформулируйте теорему о почленном умножении числовых неравенств.
-
Как вы думаете, данные теоремы справедливы только для двух числовых неравенств?
-
Что значит оценить значение выражения?
9. Домашнее задание (слайд № 29)
Изучить п.30 учебника (выучить правила), №769,773
Резерв (слайд № 30)
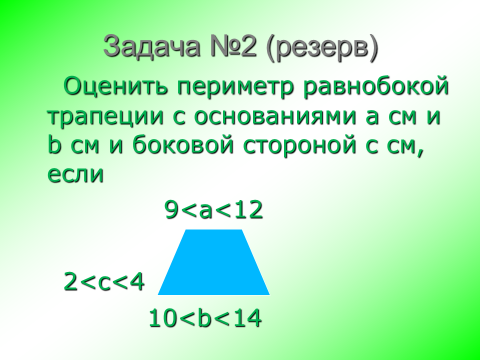
10. Рефлексия (слайд № 31)
Ученикам предлагается закончить предложения:
Я сегодня познакомился с ...
У меня сегодня получилось ...
Какие вопросы остались для меня неясными?
Ребята, готовясь к уроку, я нашла интересный факт, связанный с неравенствами. Оказывается в книгопечатании знаки и и
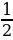
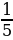
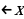
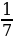
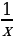
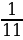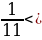
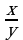
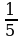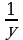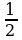
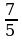Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
