Разработка урока по теме «Основные понятия стереометрии. Аксиомы стереометрии и следствия из них» (+ работа в GeoGebra)

1.

Тема учебного занятия с указанием класса

Разработка урока по теме

«Основные понятия стереометрии.

Аксиомы стереометрии и следствия из них», геометрия, 10 класс.

2.

Предметные и метапредметные результаты обучения

Цель урока: познакомить учащихся с аксиомами стереометрии и простейшими следствиями из них.

Ожидаемые результаты:

Сформировать представление об основных понятиях и аксиомах стереометрии.

Учащиеся должны знать:

• аксиомы стереометрии;

• следствия из аксиом стереометрии и их доказательство.

Учащиеся должны уметь:

• применять аксиомы стереометрии и следствия из них при решении задач;

• выявлять общие и различные черты между аксиомами планиметрии и стереометрии;

• освоение способов переработки информации: анализа, систематизации, классификации и др.;

• знать связь между разделами геометрии;

• уметь определять объекты стереометрии, правильно их обозначать и строить;

• знать способы построения прямой в пространстве;

• определять взаимное расположение прямых в пространстве;

• решать простейшие задачи на применение аксиом стереометрии;

• представлять информацию в корректной форме.

Тип урока: объяснение нового материала

3.

Этапы учебного занятия с описанием:

- учебных заданий,

- форм работы на разных этапах учебного занятия,

- примеров индивидуализации учебных заданий

Ход урока.

1. Организационный момент.

Проверить готовность класса к уроку.

2. Постановка целей и задач урока.

Эпиграфом к уроку является высказывание Конфуция: «Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый лёгкий и путь опыта – это путь самый горький», его мысль продолжил советский математик Маркушевич Алексей Иванович: «Через математические знания, полученные в школе, лежит дорога к огромным, почти необозримым областям труда и открытий».

Я предлагаю вам сегодня сделать небольшие открытия по теме «Аксиомы стереометрии и простейшие следствия из них».

3. Объяснение нового материала (по группам)

Перед началом работы я предлагаю разбиться на 4 группы.

Работа в экспертных группах:

Предлагаю вам занять свои места в экспертных группах.

При работе в экспертных группах вы разбираете одну часть темы. Ваша задача осмыслить информацию, обсудить её в группе, разобраться во всех вопросах так, чтобы затем вы смогли своим одноклассникам объяснить материал (1 этап)

1 группа – Введение в стереометрию.

2 группа – Аксиомы планиметрии

2. Аксиомы планиметрии.

Аксиома (др.-греч. ἀξίωμα — утверждение, положение) — утверждение, принимаемое истинным без доказательств, которое в последующем служит «фундаментом» для построения доказательств.

Аксиомы принадлежности.

• Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

• Через любые две точки можно провести прямую, и только одну.

Аксиомы расположения.

• Из трех точек на прямой одна и только одна лежит между двумя другими.

• Прямая разбивает плоскость на две полуплоскости.

Аксиомы измерения.

• Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумму длин частей, на которые он разбивается любой его точкой.

• Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусов. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиомы откладывания.

• На любой полупрямой от ее начальной точки можно отложить отрезок, заданной длины, и только один.

• От любой полупрямой в заданную полуплоскость можно отложить угол заданной градусной мерой, меньшей 180 градусов, и только один.

• Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Аксиома параллельности.

• Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

В аксиомах никогда не включаются логические цепочки, доказательства и построения. 

3 группа – Аксиомы стереометрии

/

4 группа – Взаимное расположение прямых в пространстве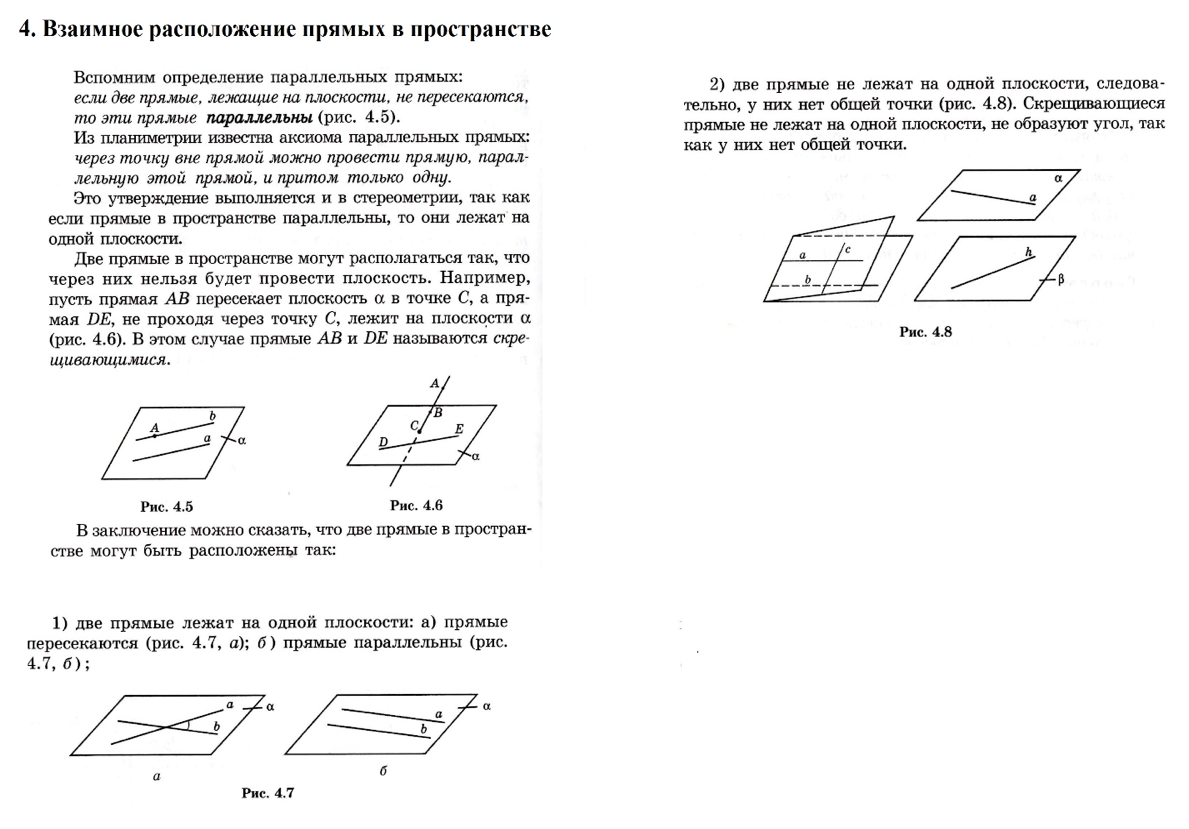

После разбора тем, задаются ключевые вопросы к группам(2 этап):

1 группа. Связаны ли между собой планиметрия и стереометрия?

2 группа. Изменить аксиомы планиметрии так, чтобы их можно было применить в пространстве.

3группа. В каком случае можно провести плоскость в пространстве? (рассмотрите все варианты)

4группа. Определите условие параллельности прямых в пространстве.

Далее предлагаются задачи для решения (3 этап):

Задачи

1. Каким плоскостям принадлежат:

прямая АВ____________________

/ В₁ С₁

точка D₁ _____________________

А₁

D₁

В С

А

D

2. Через точку плоскости проведена прямая. Каким может быть взаимное расположение плоскости и этой прямой? Сделайте рисунки.

3. Через середины сторон треугольника проведена плоскость. Совпадает ли она с плоскостью треугольника? Покажите на рисунке.

4. На плоскости проведена прямая а и взята точка А, лежащая на прямой. Через точку А проведена прямая с. Каким может быть взаимное расположение прямых а и с? Покажите на рисунке.

Дополнительное задание (2 час геометрии)

Визуализация стереометрических объектов с помощью ПО GeoGebra

Цель: познакомить с построением геометрических моделей с помощью ПО GeoGebra

Задачи:

- формирование у учащихся умения строить геометрические модели в системе автоматического проектирования GeoGebra, через построение геометрических объектов.

- развить познавательные интересы, навыки работы с мышью и клавиатурой, самоконтроль.

- воспитание информационной культуры учащихся, внимательности, аккуратности, дисциплинированности, усидчивости.

Учащимся предлагается решить задачу №2 из учебника с помощью программы GeoGebra (учащиеся уже знакомы с этой программой и умеют с ней работать), необходимо перенести рис.9 из учебника в программу и ответить на поставленные в задаче вопросы.

(задача №2: по рис.9 назовите: а) точки лежащие в плоскостях DCC1 и BQC; б) плоскости, в которых лежит прямая AA1; в) точки пересечения прямой MK с плоскостью ABD, прямых DK и BP с плоскостьюA1B1C1; г) прямые, по которым пересекаются плоскостиAA1B1 и ACD, PB1C1 и ABC; д) точки пересечения прямых MK и DC, B1C1 и BP, C1M и DC.

Пример работы учащихся: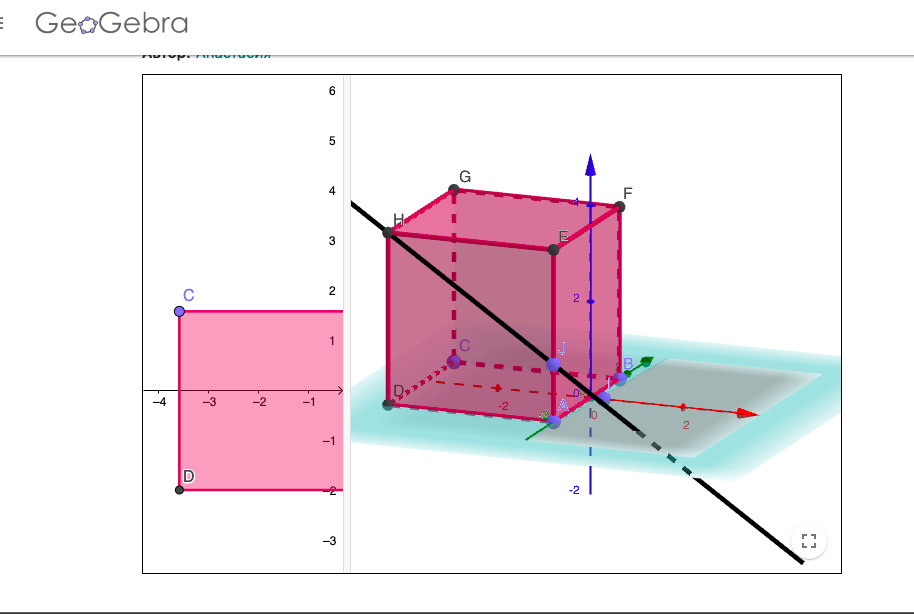

4.

Перечень формируемых УУД

Личностные УУД:

Ученикам дается задание, решение которого надо обосновать, основываясь только на фактах.

Познавательные УУД:

Учащимся даются задания на выдвижение гипотезы, задание на доказательство какого-либо суждения, решение текстовых задача по алгоритму.

Коммуникативные УУД:

Учащиеся работают в группах, во время урока дискуссия, обсуждение нового материала,

Регулятивные УУД:

В начале урока постановка учебной задачи, формулирование цели урока.

5.

Формы организации учебной деятельности

Формы организации деятельности учащихся: фронтальная, работа в группах, работа на компьютерах

6.

Формы оценивания и примеры заданий для оценивания

Оценочный лист группы № __________________________________

Критерии к 1-2 этапам (максимум 4 балла):

1. Ценность предложенной информации.

2. Активность в обсуждении.

3. Полнота изложения.

4. Участие в презентации работы.

Критерии к 3 этапу (максимум 3 балла):

1. Активность в обсуждении.

2. Правильность решения.

3. Участие в презентации работы.

Шкала перевода балла в оценку:

9 - 11 баллов – «5»,

7-8 баллов – «4»,

5-6 баллов – «3»,

менее 5 баллов – «2»