Дата: 10.10.2013 Класс:11г Скалярное произведение векторов. Угол между векторами.
Цели:
обобщить понятие «угол между векторами», научить находить угол между векторами (в пространстве).
развивать логическое мышление;
воспитывать внимательность.
Ход урока
I. Организационный момент
II. Устная работа.
2. ABCD – ромб.  BAC = 30°.
BAC = 30°.
III. Объяснение нового материала построить в соответствии с п. 46.
Показать пример нахождения углов между векторами на стереометрических моделях (обратить внимание на векторы, лежащие на скрещивающихся прямых).
IV. Решение задач: № 442, 507, 508.
Домашнее задание: теория (п. 50), № 441, на повторение – № 490, 491 (устно), 492, 501.
Дата: 16.10.2013 Класс: 11г
Тема: СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Цель:
проверить навык нахождения углов между векторами, обобщить понятие «скалярное произведение векторов».
развивать память, мышление;
воспитывать организованность.
Ход урока
I. Организационный момент
II. Актуализация знаний.
1) Проверка домашнего задания
2) решить №507
III. Объяснение нового материала
1)Определение скалярного произведения векторов
2) Рассмотреть случай, когда скалярное произведение ненулевых векторов равно о.
3) Рассмотреть скалярный квадрат вектора
4) Вычисление скалярного произведения векторов по их координатам
5)Рассмотреть утверждения 1-4
IV. Решение задач: №№ 443, 444, 445 (а, в, д), 446, 448.
Домашнее задание: теория (п. 50–51), №№ 445 (б, г), 447, 449, 506.
Дата:17.10.2013 Класс:11г
Простейшие задачи в координатах. Скалярное произведение векторов
Цель:
сформировать навык вычисления углов между векторами, прямыми и плоскостями.
развивать логическое мышление;
воспитывать организованность.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Запомните пропуски, чтобы получить верное высказывание.(карточки по вариантам)
III. Объяснение нового материала.
А. Алгоритм нахождения угла между векторами  {x1; y1; z1} и
{x1; y1; z1} и  {x2; y2; z2}, заданными своими координатами.
{x2; y2; z2}, заданными своими координатами.
1. Вычислить длины векторов  и
и  :
:
, .
2. Найти скалярное произведение  :
:
 = x1 ∙ x2 + y1 ∙ y2 + z1 ∙ z2.
= x1 ∙ x2 + y1 ∙ y2 + z1 ∙ z2.
3. Найти косинус угла α между векторами  и
и  по формуле:
по формуле:
cos α = .
.
Примеры.
1. (№ 451 (д)).  {
{ ; –
; – ; 2},
; 2},  .
.
Найдите угол между векторами  и
и  .
.
1)  .
.  .
.
2) – 2 ∙ 1 = –1 – 1 – 2 = –4 .
3) cos α = = –1
= –1  α = 180°.
α = 180°.
2. (аналогичный № 453).
Даны точки A (1; 3; 0), B (2; 3; –1), C (1; 2; –1). Найдите угол между 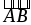 и
и  .
.
1) A (1; 3; 0), B (2; 3; –1) 
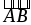 {2 – 1; 3 – 3; –1 – 0}.
{2 – 1; 3 – 3; –1 – 0}.
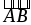 {1; 0; –1}
{1; 0; –1}  .
.
A (1; 3; 0), C (1; 2; –1) 
 {1 – 1; 2 – 3; –1 – 0}.
{1 – 1; 2 – 3; –1 – 0}.
 {0; –1; –1}
{0; –1; –1} 
 =
= .
.
2) 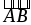 {1; 0; –1},
{1; 0; –1},  {0; –1; –1}
{0; –1; –1} 
 = 1 ∙ 0 + 0 ∙ (–1) + 1 ∙ 1 = 1.
= 1 ∙ 0 + 0 ∙ (–1) + 1 ∙ 1 = 1.
| 3) cos α =  cos α = 60°. cos α = 60°. Найдите угол между 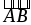 и и  . . α = 180° – 60° = 120°. | 
|
В. Нахождение угла между прямыми.
Ввести понятие направляющего вектора прямой.
Так как угол между прямыми принято считать острым, то
cos α = , где
, где  и
и  – направляющие векторы прямых.
– направляющие векторы прямых.
Пример (№ 464 (а)). Вычислите угол α между прямыми 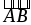 и
и  , если A (3; –2; 4), B (4; –1; 2), C (6; –3; 2), D (7; –3; 1).
, если A (3; –2; 4), B (4; –1; 2), C (6; –3; 2), D (7; –3; 1).
1. 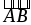 {1; 1; –2}, .
{1; 1; –2}, .
 {–1; 0; 1},
{–1; 0; 1},  .
.
2.  = 1 ∙ (–1) + 1 ∙ 0 – 2 ∙ 1 = –3.
= 1 ∙ (–1) + 1 ∙ 0 – 2 ∙ 1 = –3.
3. cos α =α = 30°.
С. Нахождение угла между прямой и плоскостью.
| | Пусть  {x1; y1; z1} направляющий вектор прямой a. {x1; y1; z1} направляющий вектор прямой a. Вектор  {x2; y2; z2} – ненулевой вектор, перпендикулярный к плоскости α. {x2; y2; z2} – ненулевой вектор, перпендикулярный к плоскости α. sin α = cos β = . . |
Пример (№ 469 (а)).
| | Дано: ABCDA1B1C1D1 – куб,
AC  BD = N, M BD = N, M  A1D1, A1M : MD1 = A1D1, A1M : MD1 =
= 1 : 4. Вычислить sin (MN, (ABC)). (MN, (ABC)). |
Решение
1. Введем систему координат.
2. Пусть AB = a. Тогда B (0; 0; 0), A (a; 0; 0), A1 (a; 0; a), C (0; a; 0),
N , M  .
.
3. .
4.  {0; 0; a}.
{0; 0; a}.
5. .
6. .
Домашнее задание: теория (п. 51), №№ 451, 453, 464 (б, в, г), 469 (б, в).
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
|
2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… |
2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3.  . Длина вектора равна… . Длина вектора равна… | 3.  . Длина вектора равна… . Длина вектора равна… |
| 4. A (2; 7; 9), B (–2; 7; 1). Координаты вектора 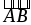 равны… равны… | 4. A (–3; 5; 5), B (3; –5; –2). Координаты вектора 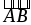 равны… равны… |
| 5. Скалярное произведение векторов  {–4; 3; 0} и {–4; 3; 0} и  {5; 7; –1} равно … {5; 7; –1} равно … | 5. Скалярное произведение векторов  {2; –8; 1} и {2; –8; 1} и  {–3; 0; 2} равно… {–3; 0; 2} равно… |
| 6. Угол между векторами  {2; –2; 0} и {2; –2; 0} и  {3; 0; –3} равен… {3; 0; –3} равен… | 6. Угол между векторами  { { ; ;  ; 2} и ; 2} и  {–3; –3; 0} равен… {–3; –3; 0} равен… |
| Вариант I | Вариант II |
| 1. Если скалярное произведение двух векторов равно нулю, то эти векторы… | 1. Если два вектора перпендикулярны, то их скалярное произведение равно… |
|
2. Если A (5; 4; 0), B (3; –6; 2) – координаты концов отрезка AB, то его середина имеет координаты… |
2. Если A (4; –4; –2), B (–8; 4; 0) – координаты концов отрезка AB, то его середина имеет координаты… |
| 3.  . Длина вектора равна… . Длина вектора равна… | 3.  . Длина вектора равна… . Длина вектора равна… |
| 4. A (2; 7; 9), B (–2; 7; 1). Координаты вектора 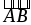 равны… равны… | 4. A (–3; 5; 5), B (3; –5; –2). Координаты вектора 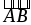 равны… равны… |
| 5. Скалярное произведение векторов  {–4; 3; 0} и {–4; 3; 0} и  {5; 7; –1} равно … {5; 7; –1} равно … | 5. Скалярное произведение векторов  {2; –8; 1} и {2; –8; 1} и  {–3; 0; 2} равно… {–3; 0; 2} равно… |
| 6. Угол между векторами  {2; –2; 0} и {2; –2; 0} и  {3; 0; –3} равен… {3; 0; –3} равен… | 6. Угол между векторами  { { ; ;  ; 2} и ; 2} и  {–3; –3; 0} равен… {–3; –3; 0} равен… |
Дата:18.10.2013 Класс:11г
Простейшие задачи в координатах. Скалярное произведение векторов
Цели:
сформировать навык вычисления углов между векторами, прямыми и плоскостями.
развивать логическое мышление;
воспитывать организованность.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
результаты проверочной работы
III. Объяснение нового материала.
А. Алгоритм нахождения угла между векторами  {x1; y1; z1} и
{x1; y1; z1} и  {x2; y2; z2}, заданными своими координатами.
{x2; y2; z2}, заданными своими координатами.
1. Вычислить длины векторов  и
и  :
:
, .
2. Найти скалярное произведение  :
:
 = x1 ∙ x2 + y1 ∙ y2 + z1 ∙ z2.
= x1 ∙ x2 + y1 ∙ y2 + z1 ∙ z2.
3. Найти косинус угла α между векторами  и
и  по формуле:
по формуле:
cos α = .
.
Примеры.
1. (№ 451 (д)).  {
{ ; –
; – ; 2},
; 2},  .
.
Найдите угол между векторами  и
и  .
.
1)  .
.  .
.
2) – 2 ∙ 1 = –1 – 1 – 2 = –4 .
3) cos α = = –1
= –1  α = 180°.
α = 180°.
2. (аналогичный № 453).
Даны точки A (1; 3; 0), B (2; 3; –1), C (1; 2; –1). Найдите угол между 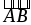 и
и  .
.
1) A (1; 3; 0), B (2; 3; –1) 
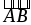 {2 – 1; 3 – 3; –1 – 0}.
{2 – 1; 3 – 3; –1 – 0}.
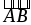 {1; 0; –1}
{1; 0; –1}  .
.
A (1; 3; 0), C (1; 2; –1) 
 {1 – 1; 2 – 3; –1 – 0}.
{1 – 1; 2 – 3; –1 – 0}.
 {0; –1; –1}
{0; –1; –1} 
 =
= .
.
2) 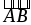 {1; 0; –1},
{1; 0; –1},  {0; –1; –1}
{0; –1; –1} 
 = 1 ∙ 0 + 0 ∙ (–1) + 1 ∙ 1 = 1.
= 1 ∙ 0 + 0 ∙ (–1) + 1 ∙ 1 = 1.
| 3) cos α =  cos α = 60°. cos α = 60°. Найдите угол между 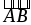 и и  . . α = 180° – 60° = 120°. | 
|
В. Нахождение угла между прямыми.
Ввести понятие направляющего вектора прямой.
Так как угол между прямыми принято считать острым, то
cos α = , где
, где  и
и  – направляющие векторы прямых.
– направляющие векторы прямых.
Пример (№ 464 (а)). Вычислите угол α между прямыми 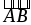 и
и  , если A (3; –2; 4), B (4; –1; 2), C (6; –3; 2), D (7; –3; 1).
, если A (3; –2; 4), B (4; –1; 2), C (6; –3; 2), D (7; –3; 1).
1. 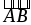 {1; 1; –2}, .
{1; 1; –2}, .
 {–1; 0; 1},
{–1; 0; 1},  .
.
2.  = 1 ∙ (–1) + 1 ∙ 0 – 2 ∙ 1 = –3.
= 1 ∙ (–1) + 1 ∙ 0 – 2 ∙ 1 = –3.
3. cos α =α = 30°.
С. Нахождение угла между прямой и плоскостью.
| | Пусть  {x1; y1; z1} направляющий вектор прямой a. {x1; y1; z1} направляющий вектор прямой a. Вектор  {x2; y2; z2} – ненулевой вектор, перпендикулярный к плоскости α. {x2; y2; z2} – ненулевой вектор, перпендикулярный к плоскости α. sin α = cos β = . . |
Пример (№ 469 (а)).
| | Дано: ABCDA1B1C1D1 – куб,
AC  BD = N, M BD = N, M  A1D1, A1M : MD1 = A1D1, A1M : MD1 =
= 1 : 4. Вычислить sin (MN, (ABC)). (MN, (ABC)). |
Решение
1. Введем систему координат.
2. Пусть AB = a. Тогда B (0; 0; 0), A (a; 0; 0), A1 (a; 0; a), C (0; a; 0),
N , M  .
.
3. .
4.  {0; 0; a}.
{0; 0; a}.
5. .
6. .
Домашнее задание: теория (п. 51), №№ 451, 453, 464 (б, в, г), 469 (б, в).







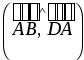 ,
, 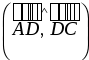 ,
,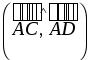 ,
,  ,
, 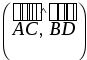 ,
,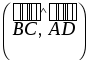 , , .
, , .









