Развитие геометрических представлений у детей старшего дошкольного возраста посредством оригами

Развитие геометрических представлений у детей старшего дошкольного возраста посредством оригами

Содержание

Введение

Глава 1. Теоретические основы использования оригами как средства развития геометрических представлений у детей старшего дошкольного возраста

1. Анализ проблемы развития геометрических представлений у детей дошкольного возраста в психолого-педагогической литературе

1.2. Особенности развития геометрических представлений у детей старшего дошкольного возраста

1.3. Использование оригами в развитии геометрических представлений у детей старшего дошкольного возраста

Глава 2. Опытно-экспериментальная работа по использованию оригами в развитии геометрических представлений у детей старшего дошкольного возраста

2.1. Изучение уровня развития геометрических представлений у детей старшего дошкольного возраста

2.2. Опытно-экспериментальная работа по использованию оригами в развитии геометрических представлений у детей старшего дошкольного возраста

2.3. Анализ результатов опытно-экспериментальной работы

Заключение

Список литературы

Приложение

Введение

Актуальность исследования. Развитие математических представлений – это чрезвычайно важная часть интеллектуального и личностного развития детей дошкольного возраста. Одной из важных задач математического развития является формирование геометрических представлений. Первые представления о форме и размерах геометрических фигур, их расположении в пространстве дети формируют именно в дошкольном детстве.

В соответствии с ФГОС ДО образовательная программа дошкольного образования должна обеспечивать познавательное развитие ребенка, предполагающее формирование первичных представлений о свойствах объектов окружающего мира (форме, размере, цвете, материале, количестве, числе, части и целом, пространстве и времени, движении и покое, причинах и следствиях и др.). В процессе ознакомления дошкольников с началами геометрии выделяется два аспекта: развитие представлений о форме предметов и геометрических фигур на сенсорной основе и развитие представлений о геометрических фигурах, их элементах и свойствах.

Над проблемой формирования геометрических представлений у детей дошкольного возраста работали следующие ученые педагоги и психологи: П. Я. Гальперин (представил опыт изучения формирования умственных действий), Т. И. Ерофеева (рассмотрены способы формирования геометрических представлений у детей дошкольного возраста), С. А. Козлова (современный взгляд на проблему математического обучения дошкольников), В. П. Новикова (предлагается методика формирования у детей 6–7 элементарных математических представлений), А. М. Пышкало (занимался проблематикой наглядных пособий по математике), Л. А. Столяр (основы ФЭМП) и многие другие.

Актуальность выбранной темы обусловлена тем, что познание геометрических фигур, их свойств и отношений расширяет кругозор детей дошкольного возраста, позволяет им более точно и разносторонне воспринимать форму окружающих предметов, что положительно может отражаться на детской познавательной деятельности в процессе интеграции образовательных областей, режимных моментах, что является основополагающим принципом ФГОС ДО.

Одним из современных средств развития геометрических представлений у детей старшего дошкольного возраста является использование оригами. Оригами помогает детям дошкольного возраста изучать и понимать многие более сложные математические и геометрические понятия. При этом кроме геометрии, оригами помогает обучить дошкольников визуализации и решению задач на моделирование.

Особенности развития математических представлений и способностей дошкольников являются предметом исследования таких авторов как А. В. Белошистая (преемственность между математическим обучения в саду и в школе), Э.Е. Браташ (связь речи и математических способностей), Л. Н. Вахрушева (диагностика математических способностей), Л. Н. Галкина (особенности конструирования), С. О. Устиненко (математические игры), Е.О. Трошина (через игровую деятельность) и т.д.

Способность визуализировать является важным навыком в дальнейшей жизни. Оригами способствует формированию наглядных математических представлений у дошкольников.

Актуальные вопросы использования оригами раскрыты в работах С. Ю. Афонькина, М. Р. Багаутдинова, В. В. Гончара, С. И. Ишимцевой, Т. Б. Сержантовой, О. А. Щегловой, Г. В. Юдиной и т.д.

Актуальность использования оригами при развитии геометрических представлений у детей старшего дошкольного возраста обусловлена тем, что в процессе преобразования плоскостей и объемных фигур ребенок оперирует геометрическими объектами, усваивает геометрические понятия, экспериментально изучает свойства фигур. В процессе складывания фигур оригами дети знакомятся с основными геометрическими понятиями (угол, сторона, квадрат, треугольник и т.д.), одновременно происходит обогащение словаря специальными терминами. Дети учатся легко ориентироваться в пространстве и на листе бумаги, делить целое на части и составлять из частей целое. Изменение геометрических фигур, их перемещение мотивирует познавательную деятельность детей.

Однако, несмотря на достаточное количество исследований в сфере развития геометрических представлений у детей старшего дошкольного возраста в настоящее время остается малоизученной проблема развития геометрических представлений у детей старшего дошкольного возраста посредством оригами. При этом применение оригами в процессе обучения способствует более эффективному усвоению дошкольниками геометрических понятий. Отсюда возникает противоречие между потенциальными возможностями применения оригами в процессе развития геометрических представлений у детей старшего дошкольного возраста и недостаточной разработанностью теории и практики по данному вопросу.

Исходя из этого противоречия, была сформулирована проблема исследования: каковы возможности оригами в развитии геометрических представлений у детей старшего дошкольного возраста.

Объект исследования – развитие геометрических представлений у детей старшего дошкольного возраста.

Предмет исследования – процесс развития геометрических представлений у детей старшего дошкольного возраста посредством оригами.

Цель исследования – теоретически обосновать развитие геометрических представлений у детей старшего дошкольного возраста посредством оригами и провести эмпирическое изучение геометрических представлений старших дошкольников.

Гипотеза исследования: предполагаем, что развитие геометрических представлений у детей старшего дошкольного возраста будет происходить более эффективно в процессе занятий, если:

• систематически и планомерно использовать технику оригами;

• включать игры с оригами в занятия;

• следовать поэтапному формированию математических представлений в различных видах деятельности с использованием оригами.

Задачи исследования:

1. Проанализировать проблему развития геометрических представлений у детей дошкольного возраста в психолого-педагогической литературе.

2. Выявить особенности развития детей геометрических представлений у детей старшего дошкольного возраста.

3. Рассмотреть возможности оригами в развитии геометрических представлений у детей старшего дошкольного возраста.

4. Изучить уровень развития геометрических представлений у детей старшего дошкольного возраста.

5. Провести опытно-экспериментальную работу по использованию оригами в развитии геометрических представлений у детей старшего дошкольного возраста.

6. Проанализировать результаты опытно-экспериментальной работы.

Методы исследования: теоретические (анализ педагогической и научно-методической литературы по теме исследования, синтез, систематизация, классификация, обобщение), практические (анализ результатов эмпирического исследования; качественное и количественное изучение данных).

База исследования: г. Сургут, Детский сад №22, «Сказка». В исследовании приняло участие 35 детей в возрасте 5-6 лет, педагоги и родители.

Структура работы. Работа состоит из введения, двух глав, заключения, списка литературы.

Глава 1. Теоретические основы использования оригами как средства развития геометрических представлений у детей старшего дошкольного возраста 1.1. Анализ проблемы развития геометрических представлений у детей дошкольного возраста в психолого-педагогической литературе

Успешное математическое развитие дошкольника в дошкольной образовательной организации (ДОО) во многом обусловлено содержанием ее познавательной деятельности.

На основании ФГОС ДО рассматривается развитие у дошкольников основных знаний, умений и навыков. Так, данный стандарт регламентирует и математическое образование дошкольников. Данное направление включено в образовательную сферу «Познавательного развития». Математическое образование в период дошкольного воспитания в соответствии с этим материалом основано на освоении параметров и свойств предметов (сенсорике), на исследовательской деятельности, на развитии познавательного интереса, на конструировании и т.д. [22].

Исследование вопросов формирования геометрических представлений у детей отражено в работах значительного количества педагогов и психологов. Исследованию этой проблемы посвящены работы отечественных педагогов и психологов: П.П. Блонского, Л.С. Выготского, Д.Б. Эльконина, А.Н. Леонтьева и др. Также данная проблема нашла отражение в историко-педагогическом контексте в исследованиях таких ученых, как Я.А. Коменский, М. Монтессори, И. Г. Песталоцци, Ф. Фребель и другие.

В настоящее время для реализации задач математического содержания необходимо учитывать принципы построения образовательного процесса:

• использование принципа вариативности;

• открытость процесса обучения;

• индивидуализация процесса обучения;

• научно-исследовательская обоснованность;

• использование в практической деятельности;

• интеграция с другими отраслями.

Математическое образование в период дошкольной работы с детьми строится на основании интеграционных процессов с другими областями развития: физического, речевого, и других. Воспитательно-образовательная работа с дошкольниками должна опираться на их возрастные и психофизиологические особенности.

На актуальность математического развития дошкольников указывают многие современные авторы и педагоги. Данный компонент является основополагающим для интеллектуальной подготовки детей, для их общего развития и формирования основных мыслительных операций. При этом по ФГОС такое направление работы в детском саду должно проводиться в рамках познавательного развития детей [7].

В работах педагогов можно найти определение понятию «математическое развитие дошкольников». Данное понятие трактуется и в рамках дошкольного образования. Содержание термина представлено в работах Е.И. Щербаковой, А.А. Столяра, А.В. Белошистой, З.А. Михайловой и т.д.

Исходя из исследований Е.И. Щербаковой, под математическим развитием дошкольников понимается сдвиг и изменение в познавательной деятельности личности, которые формируются в результате развития математических представлений и связанных с ними логических операций. Под этим понимается, что математическое развитие дошкольников представляет собой качественные изменения в формах их познавательной активности, которыми ребёнок овладевает в результате освоения элементарными математическими представлениями и связанными с ними логическими операциями.

По мнению А.А. Столяра, под математическим развитием дошкольников, следует понимать сдвиги и изменения в познавательной деятельности, которые происходят в результате формирования элементарных математических представлений и связанных с ними логических операций.

З.А. Михайлова считала, что в настоящее время, понятие «математическое развитие» тесно связано с понятием «логико-математическое развитие», которое является тождественным.

А.В. Белошистая под математическим развитием ребенка предлагает понимать, что только целенаправленное и методически организованное формирование и развитие совокупности взаимосвязанных основных свойств и качеств математического мышления ребенка и его способностей к математическому познанию действительности. В соответствии с основным содержанием ФГОС по формированию элементарных математических представлений у дошкольников можно определить основное их содержание. Представим его на рисунке 1 [6].

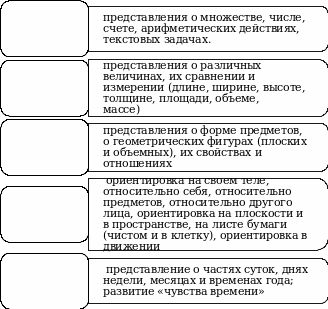
Рисунок 1. Основное содержание ФЭМП по ФГОС

В содержании ФГОС ДО математическое развитие понимается как позитивные изменения в познавательной сфере личности, которые происходят в результате освоения математических представлений и связанных с ними логических операций [32].

В содержании ФОП ДО математическое развитие понимается как процесс формирования у детей умения использовать для познания объектов и явлений окружающего мира математические способы нахождения решений: вычисление, измерение, сравнение по количеству, форме и величине с помощью условной меры, создание планов, схем, использование знаков, эталонов и др. [33].

С точки зрения Е.И. Щербаковой, в процессе развития математических представлений у детей дошкольного возраста можно выделить определенные задачи, которые будут актуальны для педагогов дошкольного образования. Представим данные задач далее на рисунке 2.

Рисунок 2. Основные задачи педагогов по развитию математических представлений у детей дошкольного возраста

Все эти задачи целесообразно решать педагогу одновременно как на занятии по математике, так и в процессе организации разнообразных видов самостоятельной деятельности детей дошкольного возраста. Многочисленные психолого-педагогические исследования и передовой педагогический опыт работы в дошкольных учреждениях показывают, что только правильно организованная деятельность воспитанников дошкольного учреждения и систематическое обучение обеспечивают своевременное математическое развитие дошкольника [25].

Е.А. Носова указывает, что в дошкольные годы желательно детей научить:

• различать геометрические формы: круг, треугольник, четырехугольник, пятиугольник и т.д., различать прямую и кривую линию.

• различать цифры в пределах 10 [29].

Л.А. Венгер, О.М. Дьяченко «предлагают математическое развитие строить таким образом, чтобы оно было направлено на развитие логического мышления, а именно на умение устанавливать простейшие закономерности: порядок чередования фигур по цвету, форме, размеру» [24].

С.Д. Луцковская изучала процесс формирования у ребенка дошкольника пространственно-временных представлений. В.А. Крутецкий, З.А. Михайлова, Е.А. Носова, М.Н. Полякова изучали развитие интеллектуальных способностей, логического и творческого мышления и выделяли компоненты математических способностей [32].

Математические представления формируются у ребенка на основе системных знаний, которые ребенок получает при взаимодействии с предметами окружающего мира, в общении со взрослыми и сверстниками. Полученные знания могут выполнять разные функции в математическом опыте детей, представим на рисунке 3.

Рисунок 3. Основные функции математических знаний для дошкольников

В контексте математического образования ребенка дошкольного возраста процесс освоения математического содержания окружающей среды должен быть целенаправленным и непрерывным. Обучение детей элементарным математическим представлениям осуществляется в условиях организованной образовательной деятельности (занятия). Вместе с тем, математическое образование дошкольников (предматематическая подготовка ребенка к школьному обучению) не предполагает прямого обучения математике, то есть занятия школьного типа [8].

Развитию математических способностей детей в дошкольном возрасте способствует развитие следующих умений:

• собирать объект из готовых частей, а также делить на составные части;

• составлять объект по заданному изображению, схеме;

• принимать пространственную позицию другого лица;

• анализировать строение конструкций;

• выполнять трансформации исходных объектов по заданным параметрам, получая новый объект с заданными свойствами;

• понимать схематическое изображение объекта, графическую модель;

• анализировать ряд объектов, находя закономерность в их изменении и продолжать ряд, придумывать ряд закономерно изменяющихся объектов;

• действовать по аналогии;

• производить операции сравнения, классификации и обобщения, самостоятельно выбирая для них основу;

• осознавать сохранение количества, тождественность, независимость, соответствие;

• правильно строить рассуждения с помощью логических связок и кванторов;

• кодировать информацию о свойствах предметов с помощью знаков-символов [26].

В соответствии с ФГОС ДО цели и задачами математического развития детей дошкольного возраста являются:

• усвоение детьми исследовательского и экспериментального способа познания математического развития;

• развитие у детей логического способа познания математических свойств и отношений, анализа, сравнения, отрицания, обобщения, классификации;

• усвоение детьми первичных математических навыков: счета, измерения, простейших вычислений;

• формирование смекалки и находчивости, сообразительности, стремления к поиску в процессе решения нестандартных задач;

• формирование речевых навыков и пополнение словарного запаса ребенка;

• формирование активной деятельности и инициативности дошкольников;

• воспитание готовности к обучению в школе: развитие навыков самостоятельности, ответственности, настойчивости в преодолении сложностей [30].

Таким образом, можно отметить, что в результате проведенного анализа литературы было определено основное определение для понятия «математическое развития дошкольников». В рамках данного исследования под этим термином можно понимать определенный объем знаний детей по ориентированию во времени и пространстве, по счету и количеству, величине и форме, а также некоторые математические способности, которые способствуют развитию у ребенка данных представлений. Геометрические представления включены в математическое развитие дошкольников.

1.2. Особенности развития геометрических представлений у детей старшего дошкольного возраста

Математическое развитие детей дошкольного возраста базируется в первую очередь на развитии простейших представлений в математике. В соответствии с таким развитием у дошкольников формируется познавательная деятельность, развиваются основные интеллектуальные способности, формируется база для дальнейшего математического развития, развивается логическое мышление.

В период дошкольного развития у детей все еще преобладает использование непроизвольного внимания. Следовательно, в этом возрасте все еще требуется демонстрация детям материала, на основе образности, яркости и наличие красочного оформления. Соответственно при просмотре дошкольники инстинктивно обращают внимание на такие составляющие демонстрируемого материала [1].

Развитие дошкольного возраста происходит в нескольких взаимосвязанных областях: физической области, когнитивной области, языковой области и социально-эмоциональной. Каждая из перечисленных областей развития влияет на другие и зависит от них [11].

Развитие всех психических процессов – ощущений, восприятия, памяти, воображения, мышления, а также развитие речи – является важной задача интеллектуального развития детей старшего дошкольного возраста. Когнитивное развитие дошкольников включает в себя также развитие речи, включая способность ребенка общаться, понимать речь и выражать свои мысли в устной форме [5].

Дети в возрасте пяти или шести лет относятся к периоду развития, который называется старший дошкольный возраст. В этот период все сферы и области личности ребенка стремительно развиваются. Также это связано и со становлением морально-нравственных норм. Дети в этом возрасте учатся доброжелательному общению, учатся понимать других, проявляют свое отношение через различные коммуникативные умения и навыки. В этот период закладываются первоначальные стратегии поведения ребенка [21].

В старшем дошкольном возрасте дети становятся более чувствительными к мнению окружающих, также в этот период формируются их личностные особенности. Все сферы развития дошкольников тесно связаны с интеллектуальным развитием и познавательными способностями. Различные проявления индивидуальности дошкольника можно отметить, как в отношениях с другими детьми, так и в отношениях со взрослыми.

Период 5-6 лет имеет весомое значение для развития мотивации учения детей, формирования различных познавательных мотивов и приобретения новых знаний. Для дошкольника становится понятным, как можно достичь успеха, как самоутвердиться в обществе.

Дети старшего дошкольного возраста способны удерживать в памяти значительный объем информации и извлекать ее в нужный момент в требуемом количестве. Именно поэтому в возрасте от 5 до 6 лет начинается период интенсивного обучения дошкольников.

Дети дошкольного возраста стремятся ко всему новому, включая также и получение новых знаний об окружающем их мире. Дошкольники отличаются значимыми изменениями в познавательной сфере. В процессе познавательной деятельности дошкольников активно развивается их память и мышление, воображение и внимание, а также другие когнитивные процессы. При проявлении интереса к окружающему миру дошкольники могут активно изучать то, что им интересно, тем самым проявляя свои исследовательские навыки. Дети активно изучают окружающие их предметы, сравнивают их, анализируют их параметры, развивают свои сенсорные способности в предметной деятельности.

У детей старшего дошкольного возраста достаточно развито восприятие предметов. Дети в этом возрасте знают основные цвета и их оттенки, хорошо воспринимают на слух различные музыкальные произведения, владеют навыками тактильного восприятия предметов. Стремительно развиваются в этом возрасте и пространственно-временные особенности восприятия. Благодаря хорошо развитым навыкам восприятия дошкольники имеют возможность изучить окружающий мир и ознакомиться с его предметами [15].

Изучением различных когнитивных процессов детей занимались Л.С. Выготский, С.Л. Рубинштейн, Б.Г. Ананьев, А.В. Запорожец, А.Н. Леонтьев, Л.А. Венгер и т.д. Авторами указывается на то, что в дошкольном возрасте у детей активно формируется произвольное внимание. Также активно развиваются все характеристики внимания: растут возможности его распределения, повышается уровень устойчивости, повышается объем.

Также в период развития старших дошкольников у них активно развивается словесно-логическое мышление. Вместе с тем получает свое дальнейшее развитие и образное мышление. При этом, в мыслительных процессах старших дошкольников все еще чаще преобладает эмоциональность, что свидетельствует о преобладающем эмоционально-образном мышлении.

Способность к логическому мышлению – универсальная человеческая черта. Логические рассуждения требуют понимания атрибутов, отношений и последовательности и важны не только в неформальном обучении, но и в повседневной деятельности. Логическое мышление ребенка является его способностью понимать и использовать правила базового логического вывода в повседневной деятельности. Мысли детей обычно эгоцентричны, то есть они видят и понимают вещи только со своей точки зрения. Этот эгоцентризм необходим для их выживания. Только после 8 лет они начинают понимать вещи с точки зрения других людей [29].

Особенности мышления в дошкольный период развития находятся в тесной взаимосвязи, различные формы и виды мышления в этот период смешиваются между собой. Именно в дошкольном образовании дети развивают различные логические операции и действия. Для педагога важно предлагать дошкольникам такие задания, которые будут способствовать формированию у детей операций сравнения, анализа, систематизации, обобщения, классификации, а также будут помогать определять различные причинно-следственные связи, делать выводы, представлять свои суждения. В итоге ребенок должен научиться самостоятельно получать новые знания, самостоятельно решать разные задачи и проблемы.

Эмоционально дошкольники развиваются в направлении большего самосознания, другими словами, осознания своих собственных эмоциональных состояний, характеристик и потенциальных действий. Также в этот период дети уже могут быть более способными различать и интерпретировать эмоции других людей, что способствует проявлению эмпатии или способности ценить чувства и восприятие других и понимать их точку зрения. Развитие эмоциональности дошкольников и их новые способности оказывают содействие в нравственном развитии детей. Дальнейший процесс формирования моральных рассуждений у детей реализуется на протяжении всего дошкольного детства. Все эти эмоциональные достижения улучшают социальные и коммуникативные способности дошкольника [19].

И.В. Тычинина изучала в своих работах математическое образование детей. Формирование элементарных математических представлений у детей основывается на определенном обследовании предметов и объектов, может сопровождаться использованием разным гипотез [13]. Автор отмечает, что на занятиях в период дошкольного развития могут быть использованы сказочные истории и рассказы, сказки. Такие произведения включают героев и сюжетную линию на основе основных понятий и математических терминов, что способствует их лучшему освоению и пониманию. В сказках дети знакомятся с определенными противоречивыми моментами, за счет решения которых дети осознают всю значимость ситуации в математике.

Дошкольное детство охватывает большую часть жизни ребенка. Данный возраст является прямым продолжением раннего возраста в сфере общей сензитивности.

Наибольший вклад в изучение старшего дошкольного возраста внесли такие ученые как Л.И. Божович, А.Н. Веракса, Л.С. Выготский, Н.И. Гуткина, В.Г. Каменская, А.Н. Леонтьев, В.С. Мухина, Д.Б. Эльконин, Г.А. Урунтаева и др.

В дошкольный период развития дети становятся более самостоятельными, у них появляется способность к объяснению того или иного своего действия. В старшем дошкольном возрасте все действия детей становятся более рациональными и благоразумными. Следовательно, у детей закладывается основа для морально-нравственного развития. Также лучше для ребенка в этом возрасте становится понятно его место в обществе, его ценность.

Внутренние убеждения дошкольника 5-6 лет формируют основу для развития волевых качеств. Для ребенка этого возраста уже становится проще рассмотреть свои действия, взять на себя ответственность и сделать определенные выводы.

Весомый вклад в изучение данных особенностей внес Л.С. Выготский. Автор рассматривал различные познавательные процессы дошкольников, а также специфику их развития на разных этапах. В выводах автора обнаруживается, что воображение дошкольника тесно связано с его чувственно-эмоциональной сферой.

Исследования педагогов и психологов указывают на то, что в старшем дошкольном возрасте у детей улучшаются коммуникативные навыки, дети обучаются групповому взаимодействию, стараются выстроить дружественные отношения со сверстниками.

Основным видом деятельности ребенка дошкольного возраста является игра, в процессе которой происходят и осуществляются основные задачи данного возрастного периода, а также происходит освоение социальных норм и правил, реализация понимания процессов межличностных взаимодействий [2].

Развитие дошкольников происходит в сюжетно-ролевой игре, в которой дети воспроизводят отношение между различными взрослыми в определенных ситуациях и часто подражают взрослым, до той стадии, на которой дошкольники воображают или представляют себе реакцию другого на свое поведение.

По мере развития детям становится доступно понимание социальных взаимоотношений, а также моральных норм и ценностей. Другими словами, взаимодействуя с ровесниками, дошкольники начинают понимать какие действия могут принести пользу или вред в той или иной ситуации. Вместе с тем детям становится доступно понимание значения определенного поступка или действия, правильное оно или неправильное.

Особенности социального взаимодействия дошкольников изучал Ж. Пиаже. С точки зрения автора, личность предрасположена к нескольким этапам морального развития. В дошкольный период развития, по мнению автора, особое влияние на ребенка имеет авторитетный взрослый. Благодаря его поведению ребенок узнает о принципах морали и нравственности, о справедливости и честности. В этот период можно говорить о гетерономной морали.

Дети дошкольного возраста стремятся ко всему новому, включая также и получение новых знаний об окружающем их мире. Дошкольники отличаются значимыми изменениями в познавательной сфере. В процессе познавательной деятельности дошкольников активно развивается их память и мышление, воображение и внимание, а также другие когнитивные процессы. При проявлении интереса к окружающему миру дошкольники могут активно изучать то, что им интересно, тем самым проявляя свои исследовательские навыки. Дети активно изучают окружающие их предметы, сравнивают их, анализируют их параметры, развивают свои сенсорные способности в предметной деятельности [3].

Основным достижением старшего дошкольного возраста является развитие основ личностной культуры ребенка, его эмоционального благополучия, развитие индивидуальных способностей и наклонностей, самостоятельности, инициативы, творчества, самодостаточности, любознательности, ответственности, коммуникативности и интеллектуальной компетентности, эти и другие личностные качества позволяют ребенку перейти в следующую возрастную группу – ранний школьный возраст – в качестве заинтересованного и познавательно мотивированного человека и избежать стрессов и разрушительных разочарований переходного периода.

В условиях развития детей дошкольного возраста педагогам важно достичь следующих целей:

• способствовать всестороннему развитию личностных качеств каждого дошкольника через самореализацию путем создания игровых и творческих ситуаций;

• развивать творчество и инициативы детей;

• формировать у дошкольников навыки коллективной и организаторской деятельности;

• обеспечивать социальную защищенность и психологический комфорт каждого дошкольника.

Для оптимального осуществления занятий педагогу важно:

• формировать ситуации успеха и положительной атмосферы;

• повышать уровень уверенности дошкольников в себе;

• способствовать использованию игр в самостоятельной деятельности;

• опираться на интересы и желания детей;

• активизировать и стимулировать познавательные способности дошкольников [9].

Развитие и степень концентрации внимания ребенка на определенных предметах или явлениях зависит в первую очередь от уровня его заинтересованности. В этот период развития внимание становится произвольным, а также подконтрольным самому ребенку. По мере развития ребенка объем его внимания увеличивается, как и период его концентрации на предмете, а также способность переключать внимание между разными предметами [4].

Итак, было определено, что особенности математического развития дошкольников основаны на психолого-педагогических и возрастных изменениях у детей дошкольников. В соответствии с таким развитием у дошкольников формируется познавательная деятельность, развиваются основные интеллектуальные способности, формируется база для дальнейшего математического развития, развивается логическое мышление. Начало формирования логического мышления у детей этого возраста способствует развитию основных мыслительных операций. Особенно ярко мышление дошкольников проявляет себя в конкретно-образном выражении. В свою очередь сам образовательный процесс оказывает активизирующее воздействие на формирование абстракций у детей, в особенности при изучении математики. В этот период для воспитания и развития дошкольников используются различные методы и способы обучения.

1.3. Использование оригами в развитии геометрических представлений у детей старшего дошкольного возраста

Оригами является практикой складывания различных изделий из бумаги. При этом оригами как традиционно японское искусство развивалось в свое время по всему миру. Исторические корни данного искусства уходят в Китай, Японию и даже в Германию.

При выполнении различных оригами, как правило, следуют определенному стандартному набору шаблонов. Но этой системе меньше 100 лет. В каждом дизайне используется один и тот же ключ, поэтому оригами может сложить не только опытный мастер, но и человек, впервые столкнувшийся с этим искусством [4].

Простота, красота и доступность оригами делают его увлекательным хобби, а также универсальным видом искусства. Понимание истории оригами помогает увидеть появление данного вида искусства в древней культуре и его развитие в настоящее время.

История оригами насчитывает почти 2000 лет. Несмотря на то, что оригами – это японское слово, которое наиболее известно как форма японского искусства, на самом деле оно было культурным наследием в Японию из Китая примерно в I веке нашей эры [2].

В Древнем Китае складывать бумагу было традицией для церемониальных целей. Китайцы в первом веке нашей эры сжигали бумагу, сложенную в виде золотых слитков, в качестве подношения умершим, и эта практика продолжается и сегодня. Такие церемониальные корни привели оригами в Японию, где его практиковали буддийские монахи.

В начале первого тысячелетия нашей эры бумага была дорогой и была доступна только элите, например монахам. Однако в 1600-х годах, в период Эдо в Японии, феодалы расширили местную промышленность. Поскольку данное расширение включало изготовление бумаги, данный материал стал намного более доступным. Однако в то время бумага все еще была предметом роскоши.

Несмотря на то, что оригами больше не ограничивалось использованием лордами и монахами, оно не было детским ремеслом, которым оно является сегодня. Навыки оригами в древности в основном использовали для подарков и церемоний [6].

Первыми известными фигурками оригами являлась пара сложенных бабочек, которые использовались в качестве украшения на свадьбе. По мере роста популярности оригами его название фактически изменилось. Сначала он был известен как «ориката», или «сложенные формы». В 1880 году название было изменено на оригами, или «сложенная бумага».

Несмотря на то, что оригами тесно связано с Японией, современное оригами на самом деле представляет собой искусство, которое развивалось по всему миру [8].

В то время как в Японии стало набирать популярность оригами, школы в Германии начали использовать бумагу для обучения своих учеников геометрии. Немецкое складывание фигурок из бумаги, хотя и не такое явно художественное, как то, что пришло из Японии, но также активно распространилось по всему миру. В нем использовались более простые углы в 45 градусов, что было проще для детей.

Немецкий стиль складывания бумаги вернулся в Японию. По сути, современное оригами представляет собой смесь этого и традиционного японского стиля [1].

В настоящее время оригами доступно каждому, во многом благодаря вкладу Акиры Йошизавы. Акир Йошизава помог стандартизировать схемы для оригами, которые сделали данное искусство доступными во всем мире [11].

На протяжении всей истории оригами люди относились к нему как к традиционному ремеслу, церемониальному подношению и забавному хобби. Но оригами также считается тонким и красивым видом искусства. Журавли из оригами являются одной из самых складываемых фигур в истории оригами.

Рисунок 4. Журавль из оригами

Однако до 1950-х годов оригами не считалось серьезным видом искусства. Из-за этого сегодня практически не существует свидетельств об оригами до 20-го века. Садако Сасаки и ее журавли продолжают вдохновлять мир и сотрудничество в международных отношениях.

В настоящее время различные новые методы складывания и материалы, а также инструменты для сохранения бумаги делают оригами более постоянной формой искусства. Из-за очень податливой природы бумаги художники-оригами постоянно расширяют границы увлекательными способами складывания.

Многие художники доводят оригами до невероятных высот. Некоторые создают органические кривые, фракталы и сферы. Другие идут еще дальше, например, создавая слонов в натуральную величину из отдельных листов бумаги [19].

В настоящее время художники складывают не только бумагу, но и другие материалы, получая поразительный эффект. В то время как некоторые художники рассматривают листы бумаги как холст, в оригами бумага является средой. Лист бумаги, как палитра красок, имеет бесконечные возможности [21].

Поскольку до 1900-х годов оригами было уделом монахов и любителей, до этого времени не существовало примечательных фигур. Поскольку оригами стало более уважаемым видом искусства, многие люди в этой отрасли приобретают известность как художники [27].

Акира Йошизава является одной из самых важных фигур в истории оригами. Известный как «Великий мастер оригами», Йошизава увлекся этим ремеслом в юном возрасте. В молодости его работа заключалась в том, чтобы обучать заводских рабочих геометрии. Акир Йошизава обратился к оригами. Незадолго до Второй мировой войны он оставил свою работу, чтобы полностью посвятить себя оригами. Акир Йошизава превратил ремесло из детского занятия в серьезное искусство. Одним из его самых значительных вкладов в оригами является система обозначений, которую сегодня используют почти все художники. В этом обозначении используется простая комбинация пунктирных линий, чтобы указать, как складывать бумагу. Он также использует стрелки, чтобы показать, где нужно складывать или переворачивать оригами [3].

Акир Йошизава также впервые применил технологию мокрого складывания, которая позволяет создавать более органичные изгибы, чем сухая бумага. Он добился успехов в оригами как в деятельности, в которой может участвовать каждый, так и в форме высокого искусства [14].

В некотором смысле, сделав оригами доступным для всех, Акир Йошизава обеспечил его выживание. В определенный момент оригами перестало быть просто хобби для детей, оно стало благодатной почвой для экспериментов художников.

Акир Йошизава создал систему обозначений или инструкции по складыванию листа бумаги в желаемую форму, известную как система Йошизавы-Рэндлетта. Пример системы Йошизавы-Рэндлетта для коробки оригами представим на рисунке 5 [22].

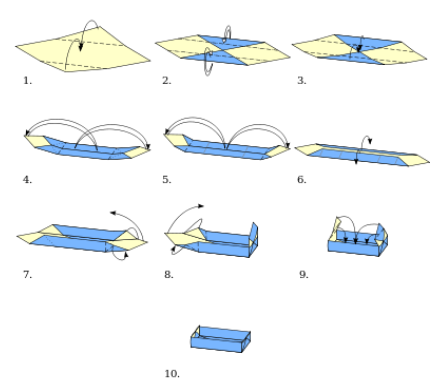
Рисунок 5. Пример разметки

На протяжении всей истории оригами также геометрия играла центральную роль, что продолжается и сегодня, когда математики используют бумагу для создания сложных форм. Роберт Дж. Лэнг, математик и художник, занимающийся оригами, является одним из таких авторов [15].

Объединив два своих увлечения, Роберт Дж. Лэнг смог создать увлекательные и реалистичные работы оригами. В то же время он использовал принципы оригами для дальнейших научных исследований.

Роберт Дж. Лэнг фокусировался на стыке науки и искусства. Он утверждал, что математика тесно связана с его искусством и определяет то, что он может делать с бумагой. Свои произведения Роберт Дж. Лэнг основывал на математических теориях.

Роберт Дж. Лэнг использовал оригами, чтобы узнать, как складывать такие конструкции, как солнечные батареи для космических кораблей. Они должны быть компактными при запуске, но разворачиваться в космосе. Математические модели помогли Роберт Дж. Лэнгу и его сотрудникам развить искусство оригами, превратив его из детского хобби в научное занятие [29].

История оригами неразрывно связана и самим образованием. Именно образование вдохновило Акиру Йошизаву на использование оригами в своей работе. Оригами полезно в качестве учебного пособия по геометрии. Но также данный вид искусства может быть основой для развития детей дошкольного возраста.

Можно отметить, что когнитивные навыки и двигательные навыки развиваются в раннем детстве. Определенные части мозга, которые контролируют эти две области, тесно связаны между собой. При этом, когда ребенок совершенствует свои моторные навыки с помощью оригами, он также тренирует свой когнитивный центр. Благодаря этой взаимосвязи такое простое и веселое занятие, как оригами, может стать очень важным для развития [9].

Оригами также помогает детям изучать и понимать многие более сложные математические понятия. Помимо геометрии, оригами учит детей визуализации и решению задач. Способность визуализировать является важным навыком в дальнейшей жизни.

Дети также могут научиться исправлять свои ошибки. Неточность может быстро испортить проект. Возможность вернуться и увидеть, где они пошли не так, и исправить их, может сделать детей более склонными к успеху, что позволяет им учиться на своих ошибках, чтобы добиться успеха в будущем [10].

В настоящее время используются различные способы складывания оригами, некоторые из них и их особенности представим:

1. Модульное – техника складывания оригами, которая складывает фигуру из нескольких листов бумаги. Лист складывается в модуль по правилу классического оригами, в дальнейшем модули соединяются друг с другом путем вкладывания. Одна из самых известных форм – кусудама (изделие с шарообразным силуэтом).

2. Складывание по развертке – один из видов оригами, применяется бумага с линиями, которые прорисованы в виде чертежа, сложений и сгибов. Чаще применяется для создания фигурок зверей и птиц.

3. Мокрое складывание – прием разработан Акирой Йошизавой. Используется смоченная бумага для создания фигур с плавными линиями, выразительностью и жесткостью. Вид оригами возник более двадцати лет назад, он является единственным способом создания трехмерных фигур, похожих на оригинал.

4. Простое оригами – вид оригами, разработанный британским оригамистом Джоном Смитом. В данной технике применяется два сгиба «гора» и «долина». Такая техника разработана для неопытных оригамистов, а также людей с ограниченными возможностями.

5. Квиллинг – трудоемкая техника, при которой необходимо из тонких скрученных полос бумаги создавать геометрические фигуры, их приклеивают на ребро бумаги к основе.

Распространенным видом оригами является модульное. При выполнении таких фигурок можно создавать различные композиции и отдельные модули из бумаги. При этом используются как большие фигуры, так и маленькие. Работа проводится без использования клея. Одним из примеров такой конструкции является оригами и его схема на рисунке 6.

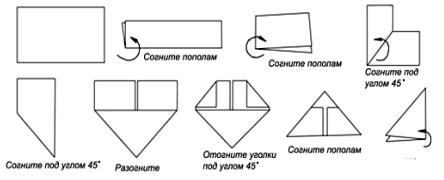
Рисунок 6. Пример использования оригами

В современном искусстве оригами есть определенные базовые фигуры, на основе которых можно сложить более сложные конструкции. В современных исследованиях и работах можно встретить различные базовые конструкции и фигуры. В результате анализа работ Т.Б. Сержантовой можно выделить следующие фигуры, представим их на рисунке 7 [24].

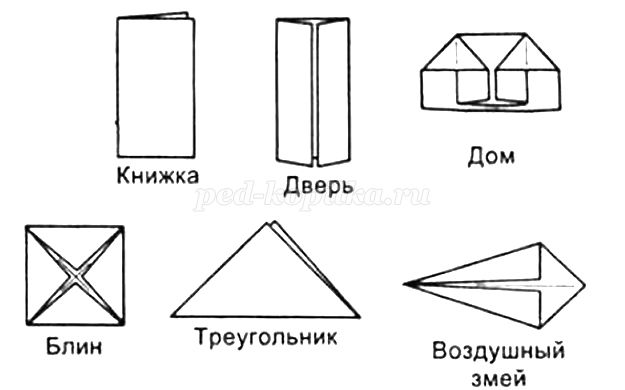
Рисунок 7. Базовые формы оригами

В современном искусстве оригами существуют различные течения и направления дальнейшего развития данного ремесла. Представим основные направления:

1. Первое направление – это классическое оригами, фигурки сложенные в традиционной манере: из квадрата, без надрезов. В классическом оригами допускается только складывание и изгибание. Простейшие способы конструирования таких фигурок основаны на умении складывать квадрат пополам по горизонтали или по вертикали и последовательном сгибании бумаги сначала вдоль, а потом поперек, подравнивая стороны к противоположным углам.

2. Второе направление – это преобразование базовых фигур, перенесение их на новые основы. Это модели, сложенные из правильного треугольника и половинки квадрата, оторванной по вертикали или диагонали, из пяти-, шести- и восьмиугольников или просто из листа писчей бумаги стандартного формата.

3. Третье направление – модульное оригами, которое нередко называют технология третьего тысячелетия. Фигура состоит из бесконечного количества одинаковых частей-модулей, которые создаются усилиями не одного человека, а целого творческого коллектива. Так, например, известная в среде оригамистов модель тиранозавра составлена из 2100 квадратов.

Превращение плоского листа бумаги в объемную фигуру является уникальным упражнением, развивающим у детей особый вид мышления. Благодаря практическим занятиям оригами дети изучают понятие симметрии и манипулируют основными геометрическими фигурами, такими как квадраты, прямоугольники и треугольники. При этом педагоги могут использовать различные образовательные приемы и методы, представим их на рисунке 8 [5].

Рисунок 8. Методические приемы

Таким образом, оригами является практикой складывания различных изделий из бумаги. При этом оригами как традиционно японское искусство развивалось в свое время по всему миру. Исторические корни данного искусства уходят в Китай, Японию и даже в Германию. При выполнении различных оригами, как правило, следуют определенному стандартному набору шаблонов. История оригами насчитывает почти 2000 лет. Акира Йошизава является одной из самых важных фигур в истории оригами. Превращение плоского листа бумаги в объемную фигуру является уникальным упражнением, развивающим у детей особый вид мышления. Благодаря практическим занятиям оригами дети изучают понятие симметрии и манипулируют основными геометрическими фигурами, такими как квадраты, прямоугольники и треугольники.

Список литературы

1. Анисимова, И. В. Использование игровых технологий в развитии геометрических представлений у детей подготовительной группы [Текст] / И. В. Анисимова // Новая наука: психолого-педагогический подход. – 2017. – № 3. – С. 5-6.

2. Афонькин, С. Ю. Все об оригами [Текст] / С. Ю. Афонькин, Е. Ю. Афонькина. – М. : ОНИКС, 2018. – 254 с.

3. Багаутдинов, М. Р. Обучение школьников бумагопластике на уроках технологии [Текст] / М. Р. Багаутдинов // Аллея науки. – 2020. – Т. 1. – № 5 (44). – С. 881-885.

4. Белошистая, А. В. Развитие математических способностей дошкольников: вопросы теории и практики [Текст] / А. В. Белошистая. – М.: Издательство Московского психолого-социального института; Воронеж: «Издательство НПО «МОДЭК», 2004. – 352 с.

5. Белькович, В. Ю. Возможности активного конструирования в образовательном процессе ДОО [Текст] / В. Ю. Белькович // Вестник ТОГИРРО. – 2018. – № 2 (40). – С. 5.

6. Блинская, Е. М. Использование логико-математических игр в работе с дошкольниками [Текст] / Е. М. Блинская // Труды Братского государственного университета. Серия: Гуманитарные и социальные науки. – 2015. – Т. 1. – С. 31-36.

7. Болотина, Л. Р. Дошкольная педагогика [Текст] / Л. Р. Болотина. – М. : Юрайт, 2020. – 219 с.

8. Борчикова, Д. Е. Развитие математических представлений детей старшего дошкольного возраста в досуговой деятельности [Текст] / Д. Е. Борчикова // Аллея науки. – 2020. – Т. 2. – № 5 (44). – С. 823-827.

9. Браташ, Э. Е. Средства развития математических представлений у детей дошкольного возраста [Текст] / Э. Е. Браташ // Международный студенческий научный вестник. – 2016. – № 5-2. – С. 56-60.

10. Бритько, Л. П. Формирование элементарных математических представлений [Текст] / Л.П. Бритько // Пралеска. – 2018. – № 2 (318). – С. 42-47.

11. Буданцева, Е. А. Математика – это интересно, поучительно, увлекательно [Текст] / Е. А. Буданцева // Традиции и новации в дошкольном образовании. – 2017. – № 4 (4). – С. 26-27.

12. Вахрушева, Л. Н. Развитие математических способностей у детей старшего дошкольного возраста [Текст] / Л. Н. Вахрушева // Научно-методический электронный журнал «Концепт». – 2016. – № S20. – С. 7–11.

13. Воронина, К. Р. Использование дидактических игр в развитии геометрических представлений у дошкольников [Текст] / К. Р. Воронина // Школа Науки. – 2020. – № 12 (37). – С. 71-72.

14. Галкина, Л. Н. Развитие математических способностей у детей дошкольного возраста [Текст] / Л. Н. Галкина // Вестник ЮУрГГПУ. – 2016. – №6. – с.32-37.

15. Гийом, Д. Оригами. Большая иллюстрированная энциклопедия [Текст] / Д. Гийом. – М. : Эксмо, 2018. – 256 с.

16. Гончар, В. В. Модульное оригами [Текст] / В. В. Гончар. – М. : Айрис-пресс, 2018. – 96 с.

17. Горев, П. М. Головоломки как средство обучения в математическом образовании детей и подростков [Текст] / П. М. Горев // Научно-методический электронный журнал Концепт. – 2018. – № 10. – С. 126-141.

18. Грайворонская, О. И. Игра «танграм» как средство развития представлений о геометрических фигурах [Текст] / О. И. Грайворонская // Дошкольное образование: опыт, проблемы, перспективы развития. – 2017. – № 1 (12). – С. 38-40.

19. Гребенникова, Н. Л. Использование моделирования в развитии математических представлений детей дошкольного возраста [Текст] / Н. Л. Гребенникова // Современные научные исследования и разработки. – 2018. – № 10 (27). – С. 269-271.

20. Гучанова, А. С. Конструктивная деятельность как средство развития творчества детей старшего дошкольного возраста [Текст] / А. С. Гучанова // Молодой ученый. – 2018. – № 43 (229). – С. 54-57.

21. Донцова, М. А. Формирование творческих способностей в конструировании и моделировании из бумаги у детей старшего дошкольного возраста [Текст] / М. А. Донцова. // Молодой ученый. – 2019. – № 9-1 (247). – С. 62-66.

22. Душаев, Г. Г. Танграм – дощечка мудрости [Текст] / Г. Г. Душаев // Юный ученый. – 2016. – № 1-1 (4). – С. 19-21.

23. Егошина, С. Н. Математическое моделирование в детском саду [Текст] / С. Н. Егошина // Молодой ученый. – 2015. – № 22-4 (102). – С. 19-31.

24. Ерошенко, Г. С. Развитие конструктивного мышления в процессе формирования математических представлений у детей дошкольного возраста [Текст] / Г. С. Ерошенко. // Новая наука: Стратегии и векторы развития. – 2016. – № 5-2 (82). – С. 46-49.

25. Заец, О. Н. Игровые технологии развития геометрических представлений у детей старшего дошкольного возраста [Текст] / О. Н. Заец // Форум молодых ученых. – 2017. – № 4 (8). – С. 265-268.

26. Иванова, Н. М. Развитие пространственно-временных ориентировок у детей старшего дошкольного возраста средствами моделирования [Текст] / Н. М. Иванова. // Вопросы дошкольной педагогики. – 2019. – № 8 (25). – С. 5-7.

27. Ишимцева, С. И. Развитие творческих способностей детей через работу с бумагой [Текст] / С. И. Имимцева // Вестник ТОГИРРО. – 2018. – № 2 (40). – С. 7.

28. Кадол, Ф. В. Повышение творческой компетенции подрастающего поколения с помощью искусства оригами [Текст] / Ф. В. Кадол // Эпоха науки. – 2021. – № 25. – С. 197-201.

29. Комарова, Т. С. Детское художественное творчество: метод. пособие для воспитателей и педагогов: для работы с детьми 2-7 лет [Текст] / Т. С. Комарова. – М. : Мозаика-Синтез, 2008. – 160 с.

30. Кошлева, Н. В. Интеллектуальные игры как средство развития математических способностей детей дошкольного возраста с 5 до 7 лет [Текст] / Н. В. Кошлева // Дошкольная педагогика. – 2019. – № 4 (149). – С. 11-13.

31. Крутецкий, В. А. Психология математических способностей дошкольников [Текст]/ В. А. Крутецкий. – М. : Институт практической психологии, 1998. – 416 с.

32. Ларина, О. В. Формирование элементарных математических представлений у детей старшего дошкольного возраста средствами занимательной математики через организацию кружка [Текст] / О. В. Ларина // Молодой ученый. – 2018. – № 46-2 (232). – С. 72-76.

33. Леденева, Е. И. Знакомство детей с оригами как частью традиционной культуры Японии [Текст] / Е. И. Леденева // Обучение и воспитание: методики и практика. – 2016. – №27. – С.45-50.

34. Маврина, И. И. Использование развивающих игр при формировании элементарных математических представлений у дошкольников [Текст] / И. И. Маврина // Молодой ученый. – 2018. – № 46 (232). – С. 304-306.

35. Некляева, Ю. Р. Игра-головоломка «танграм» в развитии математических представлений дошкольников [Текст] / Ю. Р. Некляева // Академия педагогических идей Новация. Серия: Студенческий научный вестник. – 2018. – № 5. – С. 161-169.

36. Никифорова, Н. В. Формирование геометрических представлений у дошкольников в процессе логико-математических игр [Текст] / Н. В. Никифорова // Современное образование: традиции и инновации. – 2020. – № S3-1. – С. 60-62.

37. Николаева, А. А. Ознакомление младших школьников с геометрическим материалом с помощью конструктора «липка» [Текст] / А. А. Николаева // Молодежный научный форум: гуманитарные науки. – 2016. – № 11 (39). – С. 147-151.

38. Николаева, А. В. Развитие математических способностей детей старшего дошкольного возраста посредством логических игр [Текст] / А. В. Николаева // Энигма. – 2020. – № 20. – С. 171-177.

39. Омардина, Т. В. Моделирование как средство формирования элементарных математических представлений у детей дошкольного возраста [Текст] / Т. В. Омардина // Воспитание и обучение детей младшего возраста. – 2016. – № 5. – С. 84-86.

40. Предеина, Ю. А. Социально-педагогическое значение геометрической игры для развития у дошкольников представлений о геометрических фигурах [Текст] / Ю. А. Предеина // А-фактор: научные исследования и разработки (гуманитарные науки). – 2020. – № 2. – С. 2.

41. Репина, Г. А. Формирование краеведческих представлений детей шести-семи лет средствами плоскостного и пространственного моделирования [Текст] / Г. А. Репина // Детский сад от А до Я. – 2010. – № 4 (46). – С. 133-140.

42. Рихтер, Т. В. Игровая деятельность как средство формирования математических представлений детей старшего дошкольного возраста [Текст] / Т. В. Рихтер // Аллея науки. – 2018. – Т. 1. – № 2 (18). – С. 733-736.

43. Рубинштейн, С. Л. Основы общей психологии [Текст] / С. Л. Рубинштейн. – СПб. : Питер, 2019. – 713 c.

44. Сержантова, Т. Б. 366 моделей оригами [Текст] / Т. Б. Сержантова. – М. : Айрис-Пресс, 2009. – 192 с.

45. Сержантова, Т. Б. Оригами: базовые формы [Текст] / Т. Б. Сержантова. − 2-е изд. – М. : Айрис-Пресс, 2019. − 125 с.

46. Скоморохова, А. Р. Особенности развития математических представлений у детей дошкольного возраста [Текст] / А. Р. Скоморохова // Вестник ТОГИРРО. – 2014. – № 1 (28). – С. 36-40.

47. Торохова, Г. Н. Развитие пространственных представлений у старших дошкольников средствами математического моделирования [Текст] / Г. Н. Торохова // Начальная школа плюс До и После. – 2012. – № 4. – С. 78-82.

48. Трошина, Е. О. Развитие математических способностей у детей дошкольного возраста [Текст] / Е. О. Трошина // Актуальные научные исследования в современном мире. – 2021. – № 3-6 (71). – С. 231-235.

49. Тухватуллина, Л. Р. Особенности развития математических способностей [Текст] / Л. Р. Тухватуллина // Международный журнал гуманитарных и естественных наук. – 2019. – № 3-1. – С. 97-99.

50. Устиненко, С. О. Развитие математических способностей дошкольника [Текст] / С. О. Устиненко // Педагогика: традиции и инновации : материалы V Междунар. науч. конф. (г. Челябинск, июнь 2014 г.). – Т. 0. – Челябинск : Два комсомольца, 2014. — С. 38-39.

51. Федеральный государственный образовательный стандарт дошкольного образования [Текст] / Министерство образования и науки Российской Федерации. – М. : Просвещение, 2021.

52. Щеглова, О. А. Оригами. Волшебный мир бумаги. Новая книга оригами [Текст] / О.А. Щеглова. – Ростов на/Д-М. : Владис; РИПОЛ классик, 2019. – 200 с.

53. Юдина, Г. В. Формирование у учащихся конструкторских способностей при изготовлении изделий из бумаги [Текст] / Г. В. Юдина. // Актуальные проблемы естественно-технологического образования. – 2019. – С. 251-255.