Развитие интеллектуальных и творческих способностей учащихся через решение олимпиадных задач.

Развитие интеллектуальных и творческих способностей учащихся через решение олимпиадных задач.

Добрый день, уважаемые коллеги. Сегодня хочу с вами поделиться опытом развития интеллектуальных и творческих способностей учащихся на уроках математики.

Еще в 2019 году, я как молодой учитель, задумалась о том, как замотивировать учащихся к проектной и олимпиадной деятельности. Мною была создана математическая студия «Креативити». Для ее создания мною были разработаны курсы внеурочной деятельности для 5-9 «Занимательная математика», «Решение олимпиадных задач» и для 10-11 классов гуманитарного цикла «Мировоззренческие аспекты математики».

Цель проекта: создание условий для развития творчески одаренной личности путем создания «Математической студии «Креативити» с использованием поисково-исследовательской деятельности, развития креативного мышления и метапредметного подхода в образовательном и воспитательном процессе.

Олимпиады способствуют выявлению и развитию математических способностей учащихся. Часто на уроках ученик получает, и вполне объективно, только тройки, изредка четверки и двойки. Приходит на школьную олимпиаду попробовать свои силы. Ведь это так интересно! И вдруг мы замечаем, что он неплохо решает задачи «на логику», задачи с «изюминкой», при решении которых встают в тупик многие отличники.

Подбор материала для внеурочной деятельности и для подготовки к олимпиадам является одной из форм активной работы учителя по повышению своей научно-методической квалификации. Широкое распространение получили групповые формы работы, различного рода творческие задания, различные формы вовлечения учащихся в самостоятельную, познавательную деятельности, дискуссии, диалоги, начиная с 5 класса

Как подготовиться к олимпиаде по математике для школьников?

Какую бы олимпиаду вы ни выбрали, следует придерживаться следующих общих правил подготовки:

• Ознакомьтесь с условиями участия и критериями проверки. Готовиться к математической олимпиаде проще, когда знаешь, чего от тебя ожидают. 

• Участвуйте в разных олимпиадах по математике. Это разовьёт умение работать с разными задачами и критериями, а также станет дополнительной тренировкой. 

• Не переутомляйтесь! Соблюдайте режим, правильно питайтесь, уделяйте время отдыху и физическим нагрузкам. 

• Время от времени готовьтесь к олимпиаде вместе с единомышленниками. Одна голова хорошо, а две найдут оригинальный подход к решению и вовремя обнаружат ошибку. 

Для развития логического мышления на уроках и при подготовке к олимпиадам надо:

• Применять решение упражнений, в которых встречаются взаимно обратные операции;

• Решать задачи несколькими способами, доказывать теоремы различными методами;

• Применять различные переформулировки условия задачи;

• Учить переключению с прямого ходу мыслей на обратный;

• Учить тому, какие знания, умения, навыки и в каком порядке применять в конкретной задаче и т.д.

Все задачи должны быть подобраны так, чтобы они были на развитие:

 Гибкостью ума;

 Глубины ума;

 Несколько качеств ума;

 Приема умственной деятельности анализа;

 Приема умственной деятельности классификации;

 Приема умственной деятельности сравнения;

 Приема умственной деятельности абстрагирования;

 Приема умственной деятельности аналогии.

Рассмотрим примеры задач, способствующие развитию данных качеств:

 Без карандаша и бумаги;

 Числовые головоломки;

 Некоторые старинные задачи;

 Решение задач с конца;

 Переливания;

 Знаете ли вы проценты ?;

 Арифметическая викторина;

 Рациональные числа;

Например:

С рынка возвращались две колхозницы. Одна из них спросила другую:

«Что ты продавала?» Ответ был таким: «Я продавала дыни, и получилась так, что первому покупателю я продала половину всех дынь и еще полдыни, второму – половину оставшихся у меня дынь и еще полдыни. Третьему покупателю я продала также половину оставшихся после второго покупателя дынь и еще полдыни. Больше дынь у меня не осталась». Сколько же дынь продала эта колхозница?

Переливания.

Можно ли, имея лишь два сосуда емкостью 3 и 5 литров, набрать из

крана 4 литра воды?

1. Наполнить трёхлитровую ёмкость и вылить из неё воду в пятилитровую. В последнем останется место для 2 литров. 

2. Снова наполнить трёхлитровую ёмкость и перелить в пятилитровую 2 литра, что в неё вместятся. Значит, в трёхлитровой ёмкости остаётся 1 литр. 

3. Опустошить пятилитровый сосуд и вылить в него 1 литр из трёхлитрового сосуда. Затем снова наполнить трёхлитровый сосуд и добавить к литру воды, что уже есть в пятилитровом сосуде. Получится 4 литра в пятилитровой ёмкости

Арифметическая викторина.

Пользуясь пятью двойками и знаками действий, запишите число 28. Может ли сумма трех последовательных натуральных чисел быть простым числом? А двух? А четырех?

Рациональные числа.

1 Пусть m и n - числа либо противоположные, либо равные. В каком случае m – n = 0? m – n = 2m? m – n = -2n?

2 Могут ли выражения 2 + |а| и 3 |а| + 7 принимать отрицательные

значения?

3 Указать такие значения а, при которых равенство верно:

1. |а| = −а; 2) |а| = а.

Разные задачи (арифметическая смесь).

- В записи 888888888 поставьте между некоторыми цифрами знаки сложения так, чтобы получилось в сумме 1000

- Может ли сумма 1 + 2 + 3 + … + (k – 1) + k при каком–нибудь

натуральном значении k оканчиваться цифрой 7?

- Докажите, что если сумма двух натуральных чисел меньше 13, то произведение их не больше 36.

Затруднительные положения.

Из пяти гирь одна должна быть в 10 кг. Какими должны быть остальные гири, чтобы на чашечных весах можно было определить массу грузов от 1 кг до 85кг?

Математические софизмы.

5 = 6 Попытаемся доказать, что 5 = 6 С этой целью возьмем числовое

тождество: 35 + 10 – 45 = 42 + 12 – 54 Вынесем общие множители левой и

правой частей за скобки. Получим: 5(7 + 2 – 9) = 6(7 + 2 – 9). Разделим обе

части этого равенства на общий множитель (заключенный в скобки). Получаем

5 = 6 В чем ошибка?

Задачи на планирование.

Требуется поджарить 3 ломтика хлеба. На сковороде умещались лишь два ломтика. На поджаривание ломтика с одной стороны требуется 1 мин. За какое кратчайшее время можно поджарить с двух сторон все 3 ломтика? (Время на перевертывание и перекладывание ломтиков можно в расчет не принимать).

Геометрические задачи на вычисление, доказательство, построения с препятствиями и ограничениями.

- Диагональ трапеции перпендикуляра боковой стороне; острый угол, лежащий против этой диагонали, равен 400. Найдите остальные углы этой трапеции, если длина меньшего основания ее равна длине второй боковой стороны.

- Верно ли считать четырехугольник квадратом, если его стороны имеют равные длины?

- Дан равноугольный многоугольник. Докажите, что сумма расстояний от внутренней точки его до прямых, определяемых сторонами многоугольника, постоянна.

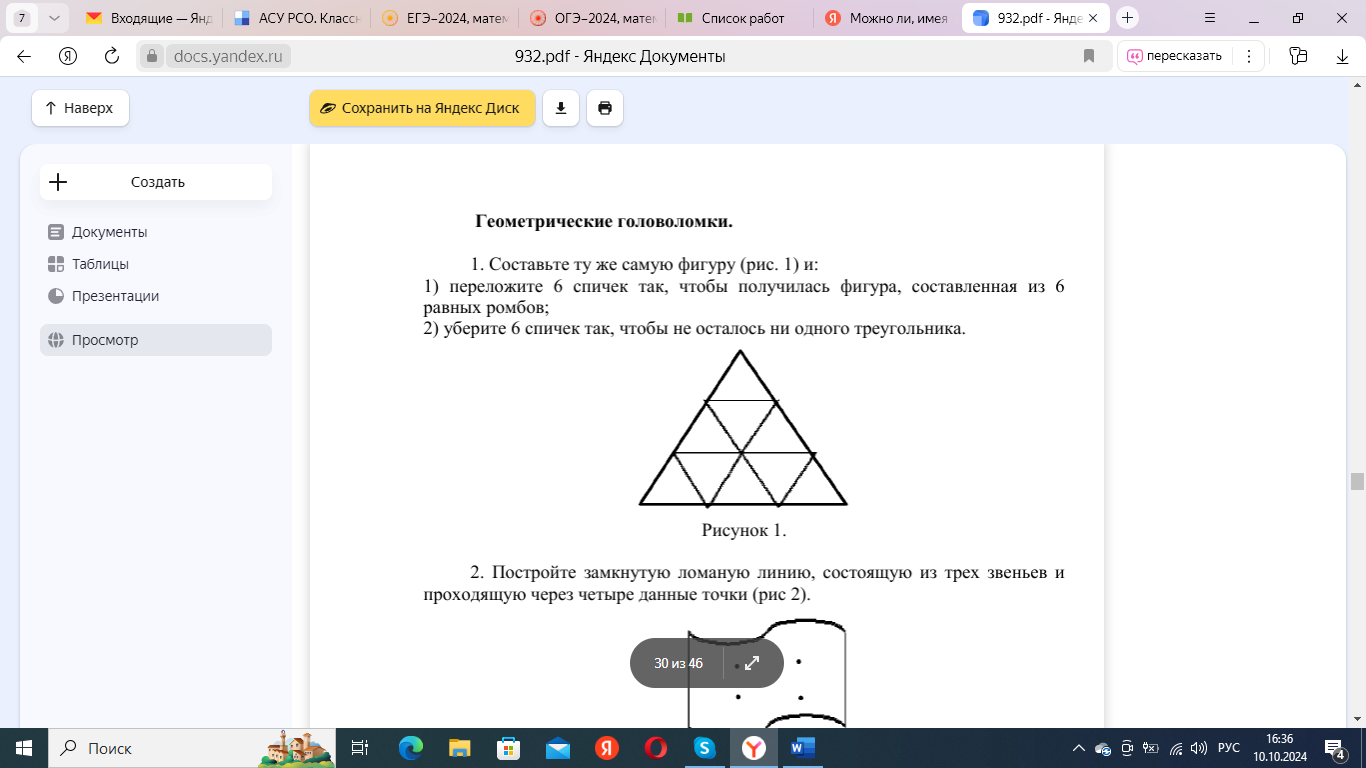
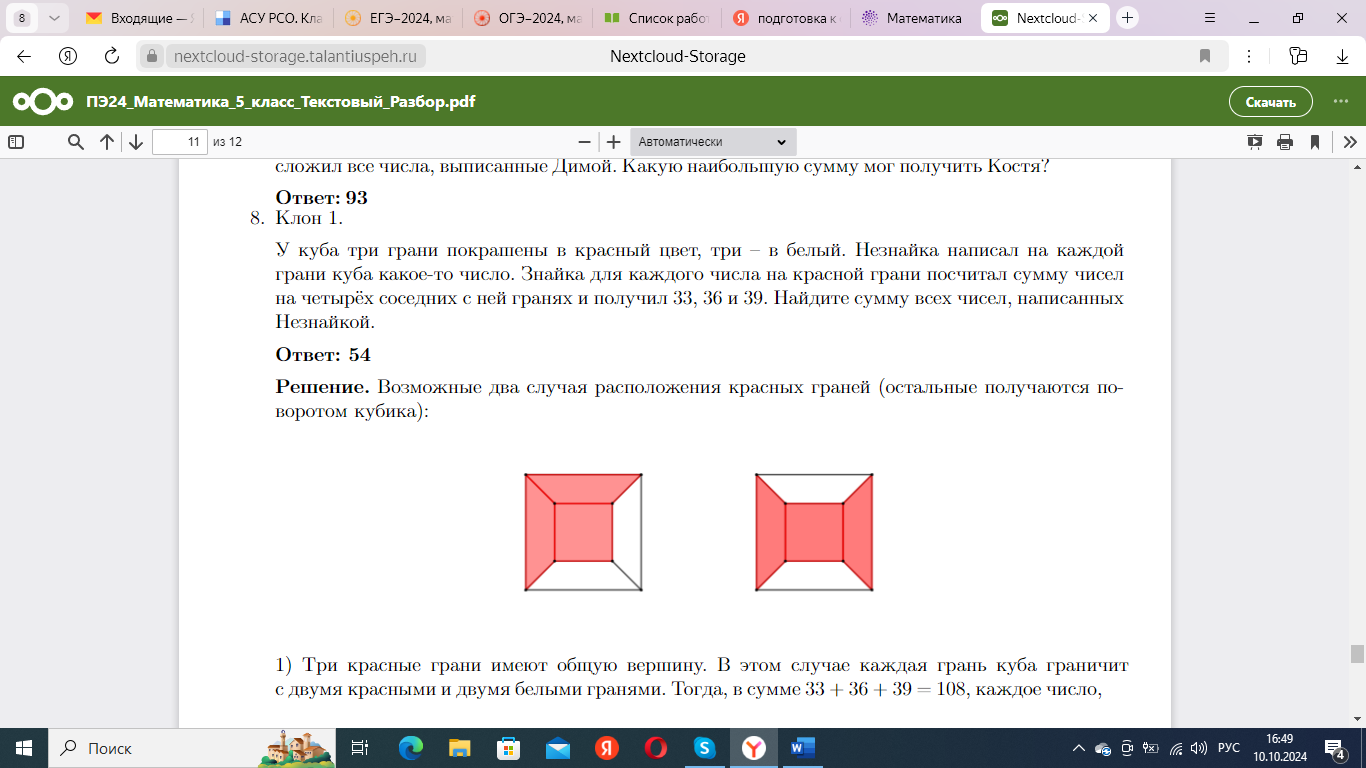
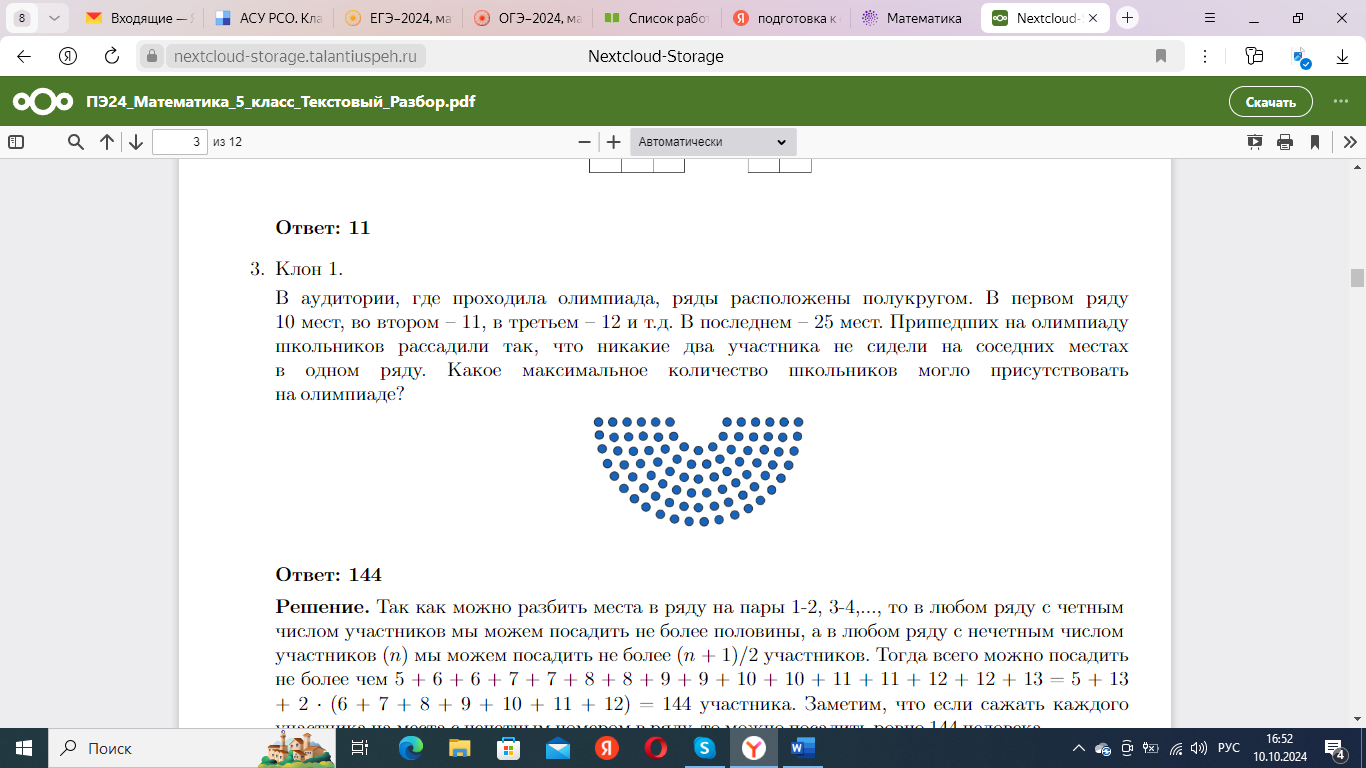
Часто в олимпиадах встречаются задания схожие с логическими задачами Зака.

Поскольку олимпиадные задания славятся своей оригинальностью и требуют креативности в решении, единственного способа их решения не существует. Однако часто на олимпиадах встречаются задания, составленные по аналогии с прошлогодними. Следовательно, действенным способом тренировки является решение, решение и ещё раз решение заданий олимпиад прошлых лет.

Успешное участие в олимпиаде требует от школьников интеллектуальной зрелости, коммуникабельности, умения быстро принимать решения в стрессовой ситуации, оценивать новую информацию, умения сконцентрироваться на выполнении поставленной задачи. Данные качества помогут молодому человеку уверенно чувствовать себя в будущем на рынке труда.

Для подготовки к олимпиадами в помощь учителю и ученикам могут быть и интернет сайты, которые собрали в себе уже большой объем заданий разных лет: сайт Школково (платно и бесплатно), Фоксфорд (платно),

http://www.problems.ru - «Задачи» На сайте представлено более 10000 задач с математических олимпиад и вступительных экзаменов по математике и информатике. Ко многим задачам даются решения.

Сайт СИРИУС также предлагает каталог задач для подготовки ко ВОШ и разбор заданий прошлых лет https://edu.sirius.online/#/contests_page/vos

Самарский центр одаренных детей таже предлагает курсы и смены для подготовки к олимпиадам

Свой долгосрочный проект «Математическая студия Креативити» я веду с 2019 по сегодняшний день. И с уверенностью могу сказать, что он дал отличные результаты. Все виды работ, а именно: подготовка к олимпиадам, к научно-практическим конференциям, уроки на развитие ФГ, внеурочные мероприятия и т.п. были направлены на повышение интереса, и роста успеваемоти.

На протяжении трёх последних лет средний балл по предмету «математика» сохраняется на стабильно высоком уровне от 4 до 5 баллов.

• Учащиеся обучены приемам самостоятельной работы, самоконтролю, взаимоконтролю, приемам проектной деятельности.

• У учащихся развито умение анализировать и сопоставлять различные идеи, делать обоснованные выводы.

• Наблюдается рост количества участников в интеллектуально-творческих конкурсах разного уровня.

• Ежегодные победители и призеры олимпиад по математике на округе;

• Победители и призеры научно-практической конференции ВЗЛЕТ (окржной уровень)

• Победители конференции «Молодежная наука 21 века»

• Призеры Регионального марафона по ФГ

• Призеры конеренции «Математика+»

• В Международных конкурсах и олимпиадах «Олимпис», «Страна талантов», Международный дистанционный конкурс «Старт», «Я-класс», «Учи.ру»:

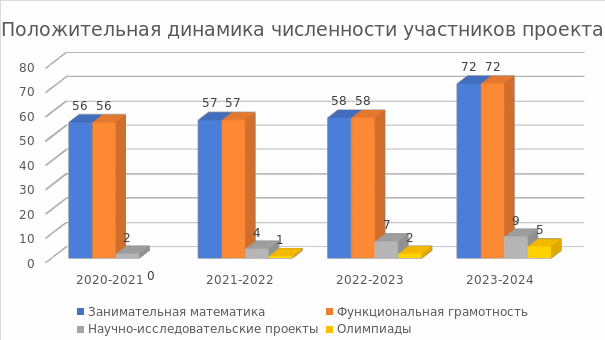
Олимпиада – это один из способов выявить учащихся, имеющих особые способности, дать им мотив и возможности для дальнейшего развития и реализации этих способностей.