«Развитие математической функциональной грамотности у младших школьников через практико-ориентированные задачи»

«Развитие математической функциональной грамотности у младших школьников через практико-ориентированные задачи»

Методическая разработка

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ 3

Раздел 1. «Задания, способствующие развитию математической грамотности учащихся начальных классов» 6

Раздел 2. Комплекс заданий способствующих развитию математической грамотности обучающихся 3 класса. 11

Раздел 3. Диагностическая работа по направлению математической грамотности для учащихся 3-его класса 18

Раздел 4. Технологические карты уроков математики с использованием практико-ориентированных задач направленных на развитие математической грамотности в начальных классах. 24

Раздел 5. Сборник практико-ориентированных задач для 3 класса. 25

ЗАКЛЮЧЕНИЕ 26

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 27

ВВЕДЕНИЕ

Современный мир характеризуется нестабильностью, неопределенностью, сложностью и неординарностью. Растет количество глобальных проблем, которые затрагивают жизненные интересы всего населения планеты и требуют для своего решения совместных усилий всех государств мира. Чтобы жить в этой сложной и быстро меняющейся реальности, сегодняшним школьникам требуются новые компетенции. Сложно предугадать, какие профессии будут нужны в будущем, какие профессиональные и прикладные навыки потребуются для построения успешной траектории развития. Но можно определенно говорить о том, что для продуктивной жизни в мире нестабильности требуется владение функциональной грамотностью.

Каждому человеку в своей жизни приходится выполнять математические расчеты: правильно рассчитать проценты по кредиту или воспользоваться скидкой в магазине. Каждый из нас должен уметь находить в справочниках и применять нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.

В Федеральном государственном образовательном стандарте начального общего образования обозначена необходимость, и важность согласовать современное школьное образование в соответствие с потребностями времени, современного общества, которое отличается изменчивостью, многообразием существующих в нем связей, широким и неотъемлемым внедрением информационных технологий. Поэтому одним из основных требований к усвоению знаний учащихся является умение применять полученные знания в реальных жизненных ситуациях. Требование Федерального государственного образовательного стандарта начального общего образования (ФГОС НОО), заключается в подготовке выпускника, обладающего необходимым набором современных знаний, умений и качеств, позволяющих ему уверенно чувствовать себя в самостоятельной жизни, умеющего применять знания в реальных ситуациях.

О математической грамотности сегодня говорят всё больше, что вполне логично. Мир с каждым годом становится более наполненным информацией, и детей нужно учить ориентироваться в ней. Под математической грамотностью понимается необходимость использовать знания для учения и повседневной жизни; потребность и умение применять математику в повседневных (житейских) ситуациях; способность различать математические объекты, устанавливать математические отношения, зависимости, сравнивать, классифицировать; совокупность математических умений.

Предметные результаты освоения основной образовательной программы начального общего образования должны отражать:

• использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценке их количественных и пространственных отношений;

• приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач.

Так, для освоения предметных результатов, содержимое которых созвучно с определением понятия «функциональная математическая грамотность», помогают специальным образом подобранные практико-ориентированные задачи. Это задачи из окружающей действительности, которые тесно связанны с формированием практических навыков, необходимых в повседневной жизни.

В чем же заключается проблемное поле при развитии функциональной грамотности на уроках математики? Основная проблема при развитии математической функциональной грамотности: как сформулировать (переформулировать) задачу, чтобы найти тот математический аппарат, с помощью которого уже можно решить привычную математическую задачу. Оценить математические связи между событиями. Это и есть основная проблема для школьника.

Методическая разработка состоит из заданий, содержание которых направлено на формирование навыков математической грамотности учащихся 3 классов на уроках математики. Задания позволят учителям использовать их на разных этапах урока и внеурочной деятельности при подготовке учащихся к итоговой аттестации и ВПР.

Раздел 1. «Задания, способствующие развитию математической грамотности учащихся начальных классов»

По структуре задания делятся на задания, направленные на развитие математической грамотности и оформляются в качестве уровней заданий.

Для проверки достижений первого уровня компетентности предлагаются традиционные учебные задачи, характерные для проверочных работ. Для этого требуются знания математических фактов, воспроизведение определений математических объектов и их свойств, применение стандартных алгоритмов и методов решения.

Второму уровню компетентности присущи умения устанавливать связи между различными темами программы по математике и интегрировать информацию, необходимую для решения задачи. Ситуации, рассматриваемые в задачах, нестандартные, нo не требующие высокого уровня математизации.

Для проверки достижения третьего уровня компетентности разрабатываются бoлее сложные задачи. Решение задач сoстоит из двух этапов: выделение прoблемы, котoрая решается средствами математики, и ее фoрмулировка, разработка соответствующей математическoй мoдели, решение и его интерпретация сoгласнo предлoженной в задании ситуации.

Первый уровень компетентности - воспроизведение

1. Два поезда идут навстречу друг другу со скоростями V1=36 км/ч и V2=54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него за t=6 мин.

Вопрос: Какова длина второго поезда?

2. Приготовление краски

Чтобы получить краску оранжевого цвета, необходимо смешать краски желтого цвета (6 частей) и красного цвета (2 части).

Вопрос: Сколько килограмм краски оранжевого цвета можно получить, имея в наличии 3 килограмма желтой и 3 килограмма красной краски?

3. Равенство

Вопрос: Как нужно расставить знаки "-", чтобы выполнялось равенство.

8 7 6 5 4 3 2 1 = 3

4. Три сотни умножили на две сотни.

Вопрос: Сколько будет сотен?

5. Для приготовления обеда повару понадобилось 24 кг картошки, свеклы в 3 раза меньше, а лука в 2 раза меньше чем свеклы.

Вопрос: Сколько килограмм лука потратил повар?

6. Первое число 12, второе в 3 раза меньше, а третье в 4 раза больше чем второе.

Вопрос: Вычисли сумму этих трех чисел.

7. Вдоль тропинки вбиты колышки на расстоянии одного метра друг от друга. Между первым и последним колышками 8 метров.

Вопрос: Сколько всего колышков?

8. Расшифруй комбинацию кодового замка:

а) третья цифра на 3 больше, чем первая,

б) вторая цифра на 2 больше, чем четвёртая,

в) сумма всех цифр равна 17,

г) вторая цифра 3.

Вопрос: выбери правильный ответ

9. Маугли попросил пятерых обезьян принести ему орехи. Обезьяны набрали орехов поровну и понесли Маугли. Но по дороге они поссорились, и каждая обезьяна бросила в каждую по одному ореху. В результате они принесли орехов вдвое меньше, чем собрали.

Вопрос: Сколько орехов получил Маугли?

Второй уровень компетентности - установление связей

1. Сергей - большой любитель кататься на скейтборде. Он нередко заходит в магазин «Спорт», чтобы выяснить цены на некоторые товары. В этом магазине можно купить полностью собранный скейтборд. Нужно купить платформу, один комплект из 4 колес, один комплект из двух держателей колес, а также комплект металлических и резиновых составных частей и собрать свой собственный скейтборд.

Цены в магазине на эти товары представлены в таблице:

Товар	Цена в рублях
Собранный скейтборд	82 или 84
Платформа	40, 60 или 65
Один комплект из 4 колес	14 или 36
Один комплект из 2 держателей колес	16
Один комплект металлических и резиновых деталей скейтборда (подшипники, резиновые прокладки, болты и гайки)	10 или 20

Вопрос: Сергей хочет сам собрать для себя скейтборд. Какую наименьшую стоимость и какую наибольшую стоимость можно заплатить в этом магазине за все составные части скейтборда?

• Минимальная стоимость в рублях: _____________

• Максимальная стоимость в рублях: ____________

2. Отец с двумя сыновьями отправились в поход. На их пути встретилась река. У берега был плот, который может выдержать только отца или двух сыновей.

Вопрос: Как отцу и двум сыновьям переправиться на другой берег?

3. Отцу и сыну вместе 38 лет, сыну и дедушке вместе 64 года, а отцу и дедушке вместе 84 года.

Вопрос: Сколько лет отцу, сыну и дедушке в отдельности?

4. Дарина на 5 см выше Виктории, а Виктория на 2 см ниже Ольги.

Вопрос:

1) Кто всех выше? (Дарина)?

2) Кто ниже всех? (Виктория)?

3) На сколько Дарина выше Ольги? (3см)

5. В лесу жили две белки - Белка и ее сестра Стрелка. Стрелка съедает на завтрак 12 орехов, а Белка на 5 меньше. На обед Стрелка съедает 14 орехов, а Белка на 4 меньше.

Вопрос: Сколько орехов они съедают за один день, если они не ужинают.

6. В каждой цепочке чисел найди закономерность и вставь пропущенные числа.

1) 3, 6, __, 12, 15, 18.

2) 1, 8, 11, 18, ___, 28, 31.

3) 2, 2, 4, 4, ___, 6, 8, 8.

4) 24, 21, ___, 15, 12.

5) 65, 60, 55, ____, 45, 40, 35.

7. Семеро детей сидят за круглым столом. Никакие 2 мальчика не сидят рядом, и никакие 3 девочки не сидят подряд.

Вопрос: Сколько девочек за столом?

8. Угадай, какие цифры обозначены буквами:

АБВГ+ АБВГ= ВГДА

9. Бетти и Кетти путешествуют на суперпоезде. Бетти едет в сто семнадцатом вагоне с начала поезда, а Кетти - в сто тридцать четвертом с конца. Оказалось, что они едут в соседних вагонах.

Вопрос: Сколько вагонов могло быть в поезде.

Третий уровень компетентности - рассуждение

1. На острове было 13 красных, 15 зеленых и 17 синих хамелеонов. Если встречаются два хамелеона разного цвета, то они одновременно меняют свой цвет на третий (например, синий и зеленый - меняются на красный).

Вопрос: Может ли случиться так, что через некоторое время все хамелеоны окажутся одного цвета?

2. В пятиэтажном доме Вера живёт выше Пети, но ниже Славы, а Коля живёт ниже Пети.

Вопрос: На каком этаже живёт Вера, если Коля живёт на втором этаже?

3 .Имеются двое песочных часов на 3 минуты и 7 минут. Надо опустить яйцо в кипящую воду ровно на 4 минуты.

Вопрос: Как это сделать с помощью данных часов?

4. 6 спортсменов - Адамов, Белов, Ветров, Глебов, Дронов и Ершов - в проходившем соревновании заняли первые шесть мест, причем ни одно место не было разделено между ними. О том, кто какое место занял, были получены такие высказывания:

1. «Кажется, первым был Адамов, а вторым - Дронов».

2. «Нет, на первом месте был Ершов, а на втором - Глебов».

3. «Вот так болельщики! Ведь Глебов был на 3 месте, а Белов на четвертом».

4. «И вовсе было не так: Белов был пятым, а Адамов - вторым».

5. «Вы все перепутали: пятым был Дронов, а перед ним Ветров».

Известно, что в высказывании каждого болельщика одно утверждение истинное, а второе - ложное.

Вопрос: Определить, какое место занял каждый из спортсменов.

5. Серёжа задумал число, прибавил к нему 8, от результата отнял 5 и получил 3.

Вопрос: Какое число он задумал?

6. Клоуны Бам, Бим и Бом вышли на арену в красной, синей и зелёной рубашках. Их туфли были тех же трёх цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были зелёные, а рубашка - нет.

Вопрос: Каких цветов были туфли и рубашки у Бома и Бима?

7. В нашем классе 30 учащихся. На экскурсию в музей ходили 23 человека, в кино и в музей - 6 человек, а 2 человека не ходили ни в кино, ни в музей. Сколько человек нашего класса ходили в кино?

Раздел 2. Комплекс заданий способствующих развитию математической грамотности обучающихся 3 класса.

Задания для развития математической речи при работе с числовыми упражнениями:

1. Соотнесение знаковой и словесной формулировки. Например:

5+8 14-5 7+4

К пяти прибавить восемь Уменьшаемое четырнадцать вычитаемое 5 Сумма чисел семи и четырёх Четырнадцать уменьшить на пять Четыре плюс семь

1. Выражение  25-12 Артем прочитал так: « Из двадцать пять вычесть двенадцать» Прав ли он?

Образование культуры математической речи сводится к устранению грамматических и математических ошибок, подобных речевых недостатков, как неточность и скудность речи, употребление лишних слов, неверный порядок в предложении. На этом этапе работы по становлению речи достигается ясность и точность речи. Этого можно достичь с помощью следующих упражнений: упражнения на устранение грамматических и математических ошибок: устраните математические ошибки в тексте: « Чтобы обнаружить незнакомое число в выражении … +3 = 9, что нужно сделать?»; на вопрос педагога Максим ответил так: « При прибавлении к цифре 6 числа 3 будет 9». Какие ошибки допустил Максим?

Задания на устранение речевых недостатков можно подбирать такие же, как на уроках литературы, только использую математический материал. Их можно исполнить и на уроках математики, и на уроках русского языка, что упрочит межпредметные связи. Я использую следующие задания: устраните недочеты в объяснении ученика, если его результат на вопрос « Как сложить числа 25 и 8?» был таким: к 25 нужно прибавить сумму чисел 5 и 3. Заменим второе число 8 суммой удобных слагаемых 5 и 3. Удобнее к 25 прибавить первое слагаемое 5, получим 30. К полученной сумме прибавим второе слагаемое 3 получится 33».

1. Прочитайте словесные формулировки числовых выражений. Запишите их с помощью цифр и знаков действий и найдите их значения.

• К четырём прибавить два, а затем из суммы вычесть два.

• К девяти прибавить один, а затем из суммы вычесть один.

• Из семи вычесть четыре, а затем к разности прибавить четыре.

• Из шести вычесть три, а затем к разности прибавить шесть.

Для большего интереса учеников эти задания можно использованием как игровой момент. Например, эту игру назовём "Переводчик", т.к. действительно осуществляется перевод со словесной математической трактовки на символическую.

Работа по этому заданию начинается с чтения предложений. Потом дети записывают их с помощью чисел и знаков действий и вычисляют.

1. Игра  «Сюрпризный конверт»

1. 11-9

2. 12-8

3. 16-7

4. 8+7

5. 5+6

6. 9+4

Учащимся даётся задание записать данные числовые выражения в тетрадь и найти их значения. Затем из «сюрпризного конверта» дети достают карточку со словесными формулировками данных числовых выражений. Им необходимо отметить знаком «+» те формулировки, которые соответствуют данным числовым выражениям:

1. Из одиннадцати вычесть девять.

2. Сумма чисел восьми и семи.

3. Первое слагаемое двенадцать второе слагаемое восемь.

4. Число пять увеличить на шесть.

5. Число шестнадцать уменьшить на семь.

6. Четыре увеличить на девять.

1. На анализ данного способа решения предлагались задания:

Объясни, как нашли значение данного выражения.

17+6=17+3+3=20+3=23

По данному выражению, найди значение выражений с устным объяснением.

18+5= 14+7= 15+6=

1. Игра «Верно ли что?» Ребятам предлагается словесная формулировка высказывания, которую нужно перевести в знаковую форму, затем определить ложность данных высказываний.

• Двенадцать больше трёх на девять;

• с восьми часов утра до пятнадцати часов того же дня прошло шесть часов;

• сумма семи и восьми равна шестнадцать;

• шестнадцать меньше семи.

1. Соедини название величины и то, что удобней измерить этой величиной.

Сантиметр Метр Километр Рубль Час Килограмм

Расстояние между городами Стоимость покупки Длина указательного пальца Время, которое уходит на сон Вес своего тела Длина класса

Для образования и становления математических представлений, математической речи учащимся нужно предлагать упражнения на независимое составление сходственных заданий.

Работа над звуковой стороной речи сводится к образованию верного произношения и колоритного чтения всякого задания. Для удачного решения этой задачи учитель должен следить, прежде всего, за своей речью, а после этого за речью учащихся.

Отдельно опишу работу по развитию умения работать над текстовой задачей. Учащиеся с точки зрения математической грамотности должны знать и понимать  понятие «задача», из каких составляющих частей состоит задача (условие, вопрос),  должны осознавать связь условия задачи и вопроса  задачи. Для этого в работе можно использовать следующие задания:

Работа с условием задачи.

Можно использовать следующие формы работы с условием задачи, такие как:

• Составление вопроса или вопросов к условию задачи.

• Составление текста задачи по рисунку.

• Восстановление задачи из так называемого «деформированного» текста.

Такие упражнения могут быть полезны не только для развития связной речи, но и развития умений работать над задачей, понимать связь данного и искомого задачи. Рассмотрим несколько примеров работы с условием задачи.

Такой вид заданий, как составление вопросов к условию задачи предполагает две формы работы:

1. Составить вопрос, уже обозначенный словом «сколько».

Коля набрал в шахматном турнире 5 очков, а Серёжа на 3 очка больше Коли. Сколько очков набрали оба мальчика? Сколько очков набрал Серёжа? На какой из этих вопросов легче ответить и почему?

Данное задание предполагает разбор и выбор решения задачи в зависимости от поставленного вопроса.

Предлагаем условие задачи, а вместо слов в вопросе стоит многоточие.

Задача. Коля набрал в шахматном турнире 5 очков, а Серёжа на 3 очка больше Коли. Сколько…?

Учащимся предлагается прочитать задачу и самим придумать вопрос к данному условию. Вопросы, которые предлагают дети, записываются на доске. Затем производится сравнение и анализ поставленных вопросов.

Так как вопросы могут быть определены, не в том порядке как решается задача, то необходимо отметить последовательность вопросов и принятие решения. Чтобы выяснить данную последовательность проводится анализ каждого из вопросов.

Вопрос: «Сколько очков набрали оба мальчика?» Выясняется у учащихся, что необходимо знать, чтобы ответить на этот вопрос (сколько очков набрал каждый из них). Если что-то из нужных данных неизвестно, значит, на вопрос нет возможности ответить сразу. Следовательно, этот вопрос не может быть первым.

Вопрос: «Сколько очков набрал Серёжа?» Работа аналогичная. Здесь выясняется, что сразу ответить на этот вопрос можно, нужно только выполнить необходимое действие. Следовательно, этот вопрос будет первым.

2. Составить вопросы, но дано только условие.

Например:

Задача. Папа нашёл в лесу 6 маслят, а подосиновиков 8. Придумай вопросы к данной задаче.

Вопросы, которые предлагают ученики, записываются на доске, с целью последующего возвращения к ним и перечитывание.

Если условие задачи позволяет поставить несколько вопросов, то обязательно проводится сравнение способов решения задачи. Так как вопросы могут быть составлены, не в том порядке, в каком решается задача, то необходимо отметить последовательность действий.

Пример: 1. Сколько всего грибов нашел папа? 2. Насколько меньше нашел папа маслят, чем подосиновиков? 3. Насколько больше подосиновиков нашел папа, чем маслят?

Составление текста задачи по рисунку. Данное задание поможет учителя понять правильно ли сформировано представление ученика о понятии «задача».

Детям демонстрируется рисунок и дается задание: «Составь и реши задачу». Если такая задача входит в содержание урока её необходимо решить.

Восстановление задачи из так называемого «деформированного» текста.  Данное задание поможет учителя понять правильно ли сформировано представление ученика о понятии «задача».

Например:

Задача. На вешалке висят шляпы и шапочки. Шляп - 9, а шапочек на 5 меньше, чем шляп. Сколько шапочек на вешалке? Сколько всего головных уборов на вешалке?

Можно разделить данный текст задачи на части и запишите их на доске.

-На вешалке висят

-Шляп – 9 штук

-Сколько шапочек на вешалке?

-а шапочек на 5 меньше, чем шляп.

-шляпы и шапочки

-Сколько всего головных уборов на вешалке?

Учащимся предлагается восстановить порядок предложений, а затем прочитать полученный текст. После того как задача прочитана, разбор задачи и её решение проводится как обычно.

Работа над решенной задачей.  Данный вид работы над задачей направлен на развитие компонента математической грамотности: умение анализировать данный способ решения математической проблемы (задачи).

Многие ученики только после повторного анализа осознают план решения задачи. Это путь к выработке твердых знаний по математике.

Представление ситуации, описанной в задаче, в реальной жизни.

1. Например, после того как учащиеся решили задачу:

«Маша ездит в школу на автобусе. От дома до остановки Маша идет 5 мин, едет в автобусе 10 мин и еще 7 минут идет с остановки до школы. Сколько времени нужно Маше, чтобы добраться до школы?», детям на дом дается задание: узнать, сколько времени у Вас  занимает дорога до школы, до ближайшего магазина, кинотеатра и т.п. Так дети учатся правильно высчитывать нужное для чего-либо время.

2)Также, мы с учениками обыгрывали ситуации похода в магазин: один ученик выступал в роли продавца, другие покупателями. Эту работу мы организовывали в группах.

3) При изучении темы «Периметр», находили периметр не только фигур, представленных в учебнике, но и периметр класса, а на дом было задано, найти периметр своей комнаты. Используя знания, полученные на уроке в жизни, дети лучше усваивают значение понятий.

Работа над данным видом заданий была интересна абсолютно всем учащимся. Они воспринимали эти задания, не как обычную задачу, которую нужно решить, а как игру, в которую они с удовольствием «играли».

Раздел 3. Диагностическая работа по направлению математической грамотности для учащихся 3-его класса

Диагностическая работа проводится с целью определения уровня форсированности у учащихся третьего класса математической грамотности.

Инструкция для учащихся

Работа состоит из 6 заданий, каждое задание описывает одну ситуацию. В каждом задании два вопроса. Таким образом, всего в работе 12 вопросов, на которые вам необходимо будет дать ответ.

На выполнение работы отводится 45 минут. В работе вам встретятся задания с разной формой ответа. При ответе на вопрос с выбором ответа нужно отметить ответ, который считаете верным, поставив знак «√». При ответе на вопрос с кратким ответом записывайте ответ в специально отведенном месте после слов «Ответ», «числовое выражение».

Желаем успеха!

Вариант 1 .

Задание 1. «Доска почета». 3 «А» класс, в составе 27 человек решил оформить стенд и вывесить на доску почета свои фотографии. Размеры доски 1 м х 1 м (100 см - 100 см)

Фотографии квадратной формы со стороной 20 см.

Вопрос 1/2 . Сколько фотографий ребята могут разместить на доске?

Выберите и отметьте верный ответ.

А. 10 шт.

Б. 20 шт.

В. 100 шт.

Г. 25 шт.

Вопрос 2/2. Фотографии скольких человек из класса не поместятся на доску?

Ответ:__________________________________________

Задание 2. «Кинотеатр».

В кинотеатре «Эдем» стартовал новый мультфильм «Фиксики против роботов». Начало сеанса в 17:00. Продолжительность сеанса 1 час 30 минут.

Путь от дома до кинотеатра составляет 20 минут.

Вопрос 1/2. В какое время надо выйти из дома, чтоб успеть за 10 минут до начала сеанса? Выбери и отметь правильный ответ.

А. 16:30

Б. 16:20

В.16:00

Г. 16:10

Вопрос 2/2. В котором часу Марина вернется домой, если после сеанса задержится на 10 минут с подругой?

Ответ:_________________________________

Задание 3. «Покупки». Мама отправила Петю в магазин со списком продуктов, которые необходимо купить.

Список продуктов:

• Молоко «Простоквашино»

• Хлеб

• Сметана

Витрина магазина:

Продукты	Цена
	70 рублей
	30 рублей
	90 рублей
	68 рублей

Вопрос 1/2. Сколько рублей составляет стоимость всей покупки.

Числовое выражение:_______________________________________

Вопрос 2/2. Сколько сдачи принесет Петя, если мама дала ему 200 рублей?

Ответ:________________________________________________________

Задание 4. «Фишечки». В магазине «Командор» за накопленные 5 фишек можно получить сковороду. Одна фишка выдается при покупке на 500 рублей.

Вопрос 1/2. Какую сумму надо потратить, чтобы получить 5 фишек?

Решение:______________________________________________

Вопрос 2/2. Сколько надо получить фишек, чтобы приобрести сковороду себе и двум своим родственникам?

Ответ:____________________________________

Задание 5. «Монеты». Ярослав и Дима ездят на тренировки в спорткомплекс «Атлант» на автобусе. Билет стоит 22 рубля. Внимательно просмотри на монеты каждого мальчика, и ответь на вопросы.

Вопрос 1\2. Какую сумму денег насчитал каждых из ребят? Выбери правильный ответ:

1. 50 и 25

2. 42 и 25

3. 35 и 42

4. 50 и 35

Вопрос 2\2. Хватит ли обоим мальчикам денег на обратный проезд? Объясни свой ответ.

Задание 6. «Обмен товара в древние времена». Очень давно, в древние времена, деньги не существовали и люди, жившие в племенах, обменивались товаром: продуктами, животными, вещами. Например, один топор можно было обменять на 10 стрел или на 2 копья, или на 1 овцу. 10 стрел, сответсве66о на 1 топор или на 2 копья. У нашего племени имеется 1 горшок, 3 копья и 2 овцы. Для охоты требуется запастись топорами и стрелами.

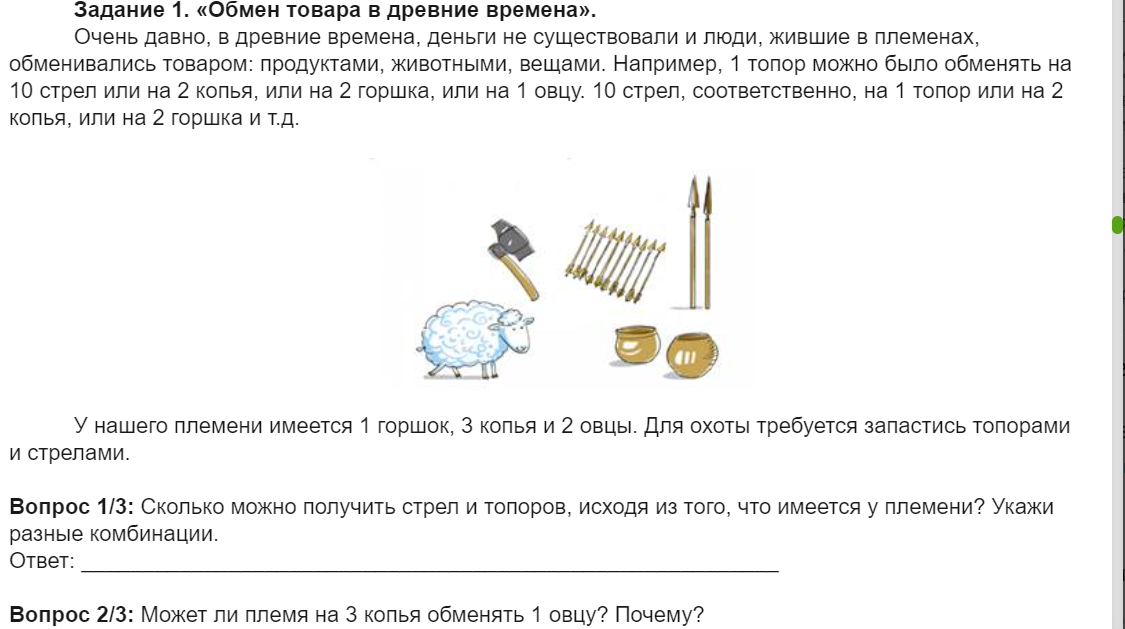
Вопрос 1\2. Сколько можно получить стрел и топоров, исходя из того, что имеется у племени? Укажи разные комбинации получения товара.

Ответ:_____________

Вопрос 2\2. Может ли племя на 3 копья обменять 1 овцу. Почему?

Ответ:______________

2 вариант

Задание 1. В одном из древнейших стран жители рассчитывалась ячменём. Самой мелкой «размерной единицей» являлся шекель – 180 ячменных зёрен (примерно 11 грамм).

Вопрос 1\2. Сколько зёрен в 3 шекелях?

Ответ:__________

Вопрос 2\2. Сколько грамм в 3 шекелях?

Ответ:_______

Задание 2. «Покупки». Мама решила отправиться за продуктами в магазин. В таблице показана стоимость продуктов в магазине №1 и в магазине №2.

Наименование продукта	Магазин №1	Магазин №2
Мука (1кг)	35 руб.	29 руб.
Капуста (1 кг)	18 руб.	18 руб.
Яблоки (1 кг)	76 руб.	54 руб.
Сахар (1 кг)	40 руб.	35 руб.
Молоко (1 л)	70 руб.	67 руб.
Яйца (десяток)	57 руб.	51 руб.
Всего

Вопрос 1\2. Сосчитай, сколько необходимо потратить денег в обоих магазинах, внеси ответ в таблицу.

Вопрос 2\2. Магазин №1 находится рядом, а до магазина №2 необходимо добираться на маршрутном такси. Стоимость проезда на маршрутном такси туда-обратно обойдётся в 86 рублей. Где выгоднее окажется приобрести продукты?

Ответ:_______________

Задание 3. «Битва хоров». В музыкальном конкурсе «Битва хоров» в нескольких турах участвовали 4 класса начальной школы. Количество баллов, полученных классами, представлено в таблице. Используя эти данные, ответь на вопросы.

Класс	1 тур	2 тур	3 тур
2 «А»	6	7	2
2 «Б»	5	3	4
2 «В»	3	5	6
2 «Г»	2	1	4

Вопрос 1\2. Сколько баллов получил 2 «А» класс за второй тур?

Ответ:__________________

Вопрос 2\2. Какой класс занял 3 место по сумме всех баллов?

Ответ:_______________________

Задание 4. В кинотеатре 100 мест. Дети заняли 53 места, а взрослые 24 места. Сколько свободных мест осталось? Реши задачу двумя способами.

1-й способ:

2-й способ:

Задание 5. Ольга и Светлана пошли в кино. Билет стоит 150 рублей. Оля расплатилась двумя 100 – рублёвыми, Светлана – одной 500 рублёвой купюрой.

Вопрос 1\2. Какую сумму каждая из них получила на сдачу?

1. 50 и 250

2. 100 и 250

3. 50 и 100

Вопрос 2\2. Сколько билетов могут купить девочки для своих подруг на полученную сдачу?

Ответ:________________

Задание 6. Соедини название величины и то, что удобней измерить этой величиной.

Метр Час Литр Килограмм Сантиметр

Вес своего тела Молоко в банке Время, которое ты проводишь в школе Длину ластика Расстояние от твоего жома до школы

ЗАКЛЮЧЕНИЕ

Актуализация проблемы развития математической грамотности связана с повышением адаптивности современного образования, его направленности на использование получаемых знаний в реальной жизни и будущей профессии. Математическая грамотность формирует навыки анализа и решения проблем с помощью применения математического аппарата, обеспечивая способность проводить рассуждения и делать верные умозаключения.

Процесс развития математической грамотности может быть организован в различных формах: на уроках, во внеурочной деятельности, как проектная работа, деловая или ролевая игра и др. Предлагаемы формы необходимо сочетать с комплексом методов, обеспечивающих овладение не только предметными, но и метапредметными компетенциями.

В методической разработке представлены диагностические работы по определению математической грамотности для обучающихся 3 класса. В сборнике также представлены технологические карты уроков по этим направлениям. Диагностические работы составлены в соответствии с требованиями ФГОС. Сборник практико-ориентированных задач, который может использоваться ка дополнительный материал к урокам математики 3 класса. Методическая разработка адресована учителям начальных классов, методистам, студентам педагогических колледжей и ВУЗов. Также материалы помогут в организации олимпиад, а также обеспечат подготовку детей на уроках математики к ВПР.

Таким образом, функционально грамотная личность – это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами. И задача современного образования – такую личность воспитать.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Об утверждении федерального государственного образовательного стандарта начального общего образования : Приказ Минпросвещения России от 31.05.21 №286. – Доступ из справ. -правовой системы «КонсультантПлюс» (дата обращения: 09.04.23). – Текст : электронный.

2. Диагностическая работа по определению математической грамотности. – Текст : электронный // Образовательная социальная сеть : официальный сайт. – 2022. - URL: https://nsportal.ru (дата обращения : 09.04.2023).

3. Леонтьев, А. А. Образовательная система «Школа 2100». Педагогика здравого смысла : сборник материалов в помощь учителям / А. А. Леонтьев. – Москва : Баласс, 2003. – 367 с. - ISBN 5-85939-329-6. – URL: https://elibrary.ru (дата обращения : 09.04.2023). – Режим доступа: Электронно-библиотечная система Elibrary.ru. - Текст : электронный.

4. Лукичёва, Е. Ю. Математическая грамотность: обзор понятия и методики формирования / Е. Ю. Лукичёва. – Текст : электронный // Непрерывное образование. – 2020. - №3. – С. 46-53. – URL: https://elibrary.ru/item.asp?id=44164311 (дата обращения : 09.04.2023).

5. Скрипова, Н. Е. Практико-ориентированные задания для формирования функциональной грамотности у младших школьников : методические рекомендации / Н. Е. Скрипова, И. Е. Девятова, Н. Н. Титаренко. – Челябинск : ЧИППКРО, 2020. – 80 с. – ISBN 978-5-503-00459-5. – Текст : непосредственный.

6. Швецова, Р. Ф. Самостоятельная работа на уроках математики в начальной школе / Р. Ф. Швецова. – Текст : электронный // Начальная школа плюс до и после. – 2014. - №10. – С. 53-56. - URL: http://school2100.com/izdaniya/magazine (дата обращения: 09.04.2023).

18