Развитие и использовании тригонометрии в средние века в разных странах

Тригонометрия (от греч. trigonon -треугольник и metrio- измеряю)

Это раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат, отвечающий практическим нуждам человека. С ее помощью можно определить расстояние до недоступных предметов и, вообще, существенно упрощать процесс геодезической съемки местности для составления географических карт. Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функция сформировались в процессе долгого исторического развития.

Тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции встречающиеся уже в III веке до н.э. в работах великих математиков– Евклида, Архимеда, Апполония Пергского.. Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией. Однако они рассматривали не линии синуса, косинуса и др., а хорды. Роль линии синусов угла a у них выполняла хорда, стягивающая дугу, равную 2 a .

Слово «тригонометрия» впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение этого слова греческое τρίγωνον – треугольник, μετρεω – мера. Иными словами, тригонометрия – наука об измерении треугольников. Тригонометрия выросла из человеческой практики, в процессе решения конкретных практических задач в областях астрономии, мореплавания и в составлении географических карт.

Развитие тригонометрии в странах Средней Азии, Ближнего Востока, Закавказья( VII - XV в.)

Развиваясь в тесной связи с астрономией и географией,- среднеазиатская математика имела ярко выраженный «вычислительный характер» и была направлена на разрешение прикладных задач измерительной геометрии и тригонометрии. Из числа сделанных ими важнейших успехов следует в первую очередь отметить введение всех шести тригонометрических линий: синуса, косинуса, тангенса, котангенса, секанса и косеканса, из которых лишь первые две были известны грекам и индийцам.

В средние века тригонометрия развивалась в Индии. Индусы употребляли половину хорды, т.е. линию синуса; они же ввели косинус. Индусам была известна формула: (которую, впрочем, не писали буквами, а выражали словами), приведение синуса и косинуса тупого угла и таблицы синусов.

В IX и X вв. арабские ученые ввели тангенс и составили более точные таблиц синусов. Развитие тригонометрии у арабов объясняется тоже потребностями астрономии и мореплавания, так как арабы вели большую торговлю по Средиземному побережью. Из арабских ученых особенно знамениты Аль-Баттани и Абд-уль-Уафа.

В Европе первым писателем по тригонометрии был английский ученый Брадвардин. Систематический курс по тригонометрии написал в XV в. Немецкий ученый Иоганн Мюллер из Кенигсберга. В книге «О треугольниках всех видов» он приводит решение плоских и сферических треугольников. Региомонтанус излагает тригонометрию уже как самостоятельную науку, независимую от астрономии.

С XVI в., после изобретения Зиетом буквенного алгебраического счисления, формулы тригонометрии принимают современный алгебраический характер. Соединение тригонометрии с алгеброй и анализом дало толчок к развитию всей математики, неразрывно связанной со всем техническим процессом. Так же по тригонометрии работали такие ученые, как: Виет (изобретатель алгебры), Романус, Нспер ( изобретатель натуральных логарифмов), Снеллиус (автор триангуляционной съемки), Потентот и гениальный математик Эйлер(введение тригонометрических функций с помощью тригонометрического круга)

Тригонометрия во всех ее проявлениях

Тригонометрия вырастала из потребностей человеческой практики (строительство. Нахождение расстояний до недоступных объектов и т. д.)

Развитию тригонометрии способствовали:

• Задачи мореплавания, требовавшие по звездам определить правильный курс корабля;
• Задачи определения по звездам пути при движении караванов в пустыне;
• Задачи земледелия, требовавшие введения точного календаря и многие другие задачи.

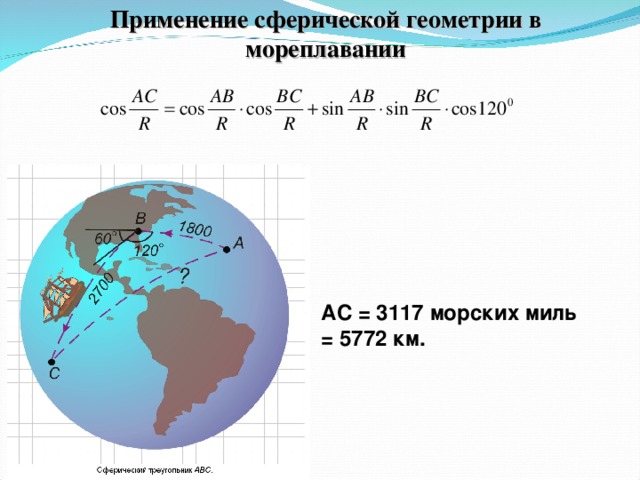
Применение сферической геометрии в мореплавании

АС = 3117 морских миль

= 5772 км.

Задача. Определить расстояние от корабля, находящегося в море, до берега.

Решение. Пусть корабль находится в точке К, а наблюдатель — в точке А . Построим прямой угол с вершиной в точке А, откладыва­ем на берегу отрезок АС и делим его пополам точкой В. Затем из точки С передвигаемся по прямой т, перпендикулярной ВС, до тех пор, пока не дойдем до точки D , из которой точки К и В видны лежащими на одной прямой. Отме­тим полученную точку как D . Прямоугольные треугольники ВС D и ВАК рав­ны, следовательно. АК=С D . а длину отрезка С D можно непосредственно измерить.

Решение задач о нахождении расстояний до не­доступных объектов, а также задач на вычисление недоступных высот было одним из источников развития тригонометрического знания.