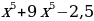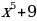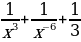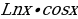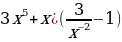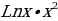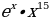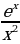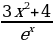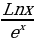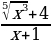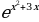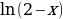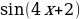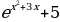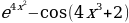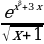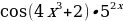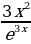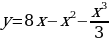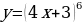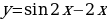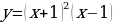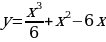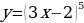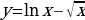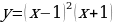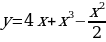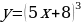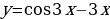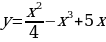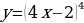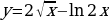Реализация индивидуальных образовательных маршрутов в работе со студентами-спортсменами
Общего требования к созданию индивидуального образовательного маршрута (ИОМ) в настоящее время не предложено. Так как для построения ИОМ необходимо учитывать особенности обучающегося и его уровень развития на протяжении определенного времени.
Из анализа опроса стало понятно, что при выборе построения индивидуальных образовательных маршрутов необходимо учитывать, что многие из студентов не берут с собой учебники и тетради. Это означает, что необходимо найти такую образовательную платформу, на которой можно будет размещать все необходимые материалы, и у студентов не будут возникать проблемы при входе на данный портал.
Таким образовательным порталом для ГБПОУ Дзержинского педагогического колледжа является платформа Moodle (сайт: https://moodle.dpk.su). К данному порталу имеют доступ все первокурсники, так как их там регистрируют в обязательном порядке.
Платформа moodle является одной из самых популярных систем электронного обучения и на ней работают крупные университеты во всем мире.
Плюсом данной платформы является создание онлайн-курсов, то есть все текстовые документы, разработанные презентации и видео уроки можно объединить в обучающий курс, который будет доступен всем студентам или конкретным курсам.
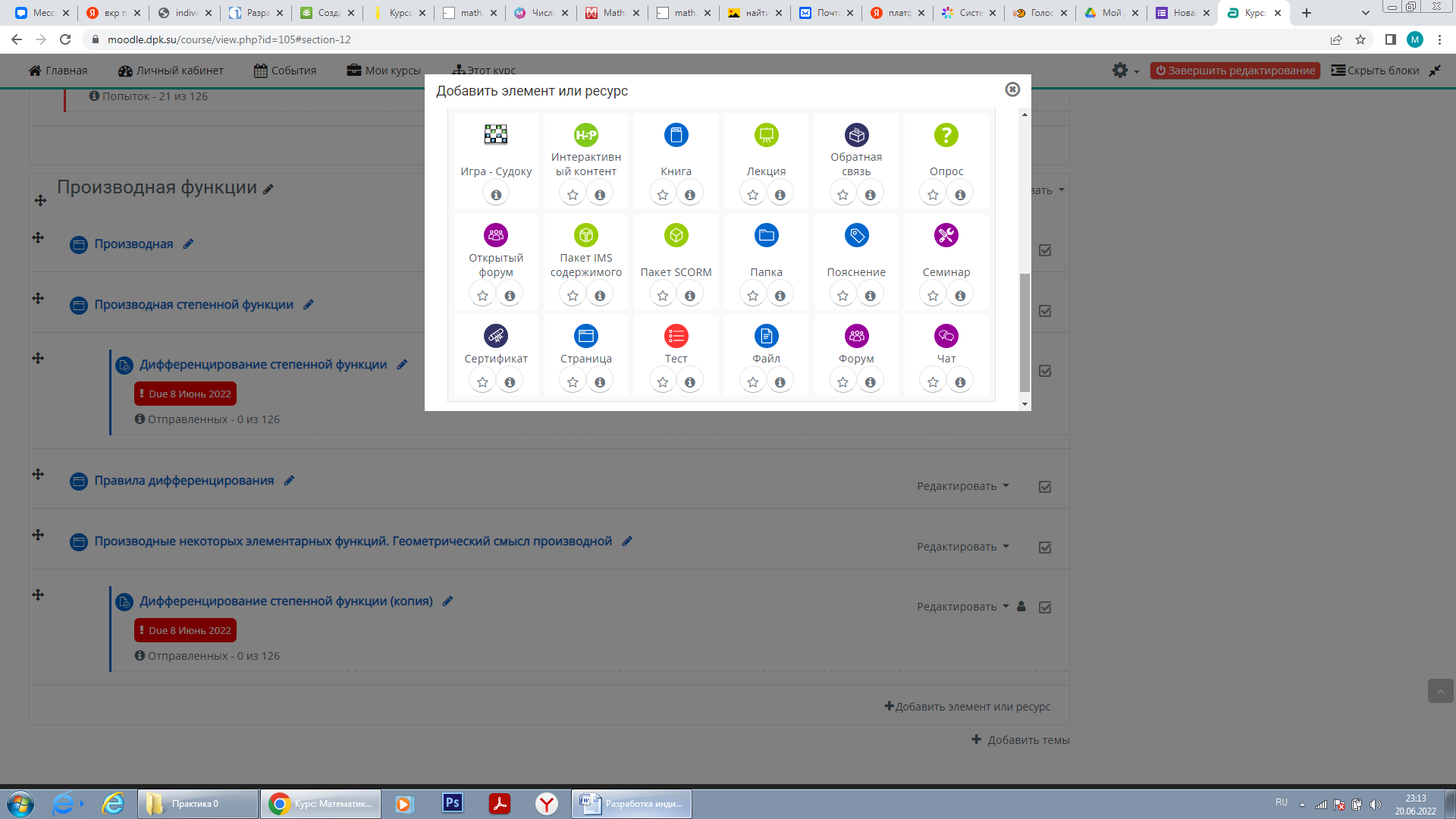
Рисунок 1. «Элементы и ресурсы платформы Moodle»
Для проверки знаний у обучающихся в Moodle предусмотрен редактор тестов (рисунок 1). В данном редакторе доступно около 15 типов заданий: от выбора одного правильного ответа до перетаскивания объектов (рисунок 2). А для того, чтобы студентам было сложнее списывать, предусмотрено ограничение времени прохождения и число попыток (рисунок 1). Неотъемлемым плюсом для преподавателя является то, что система проверяет ответы автоматически, а так же к каждому вопросу можно оставить комментарий, где можно указать ошибки, которые совершил студент.
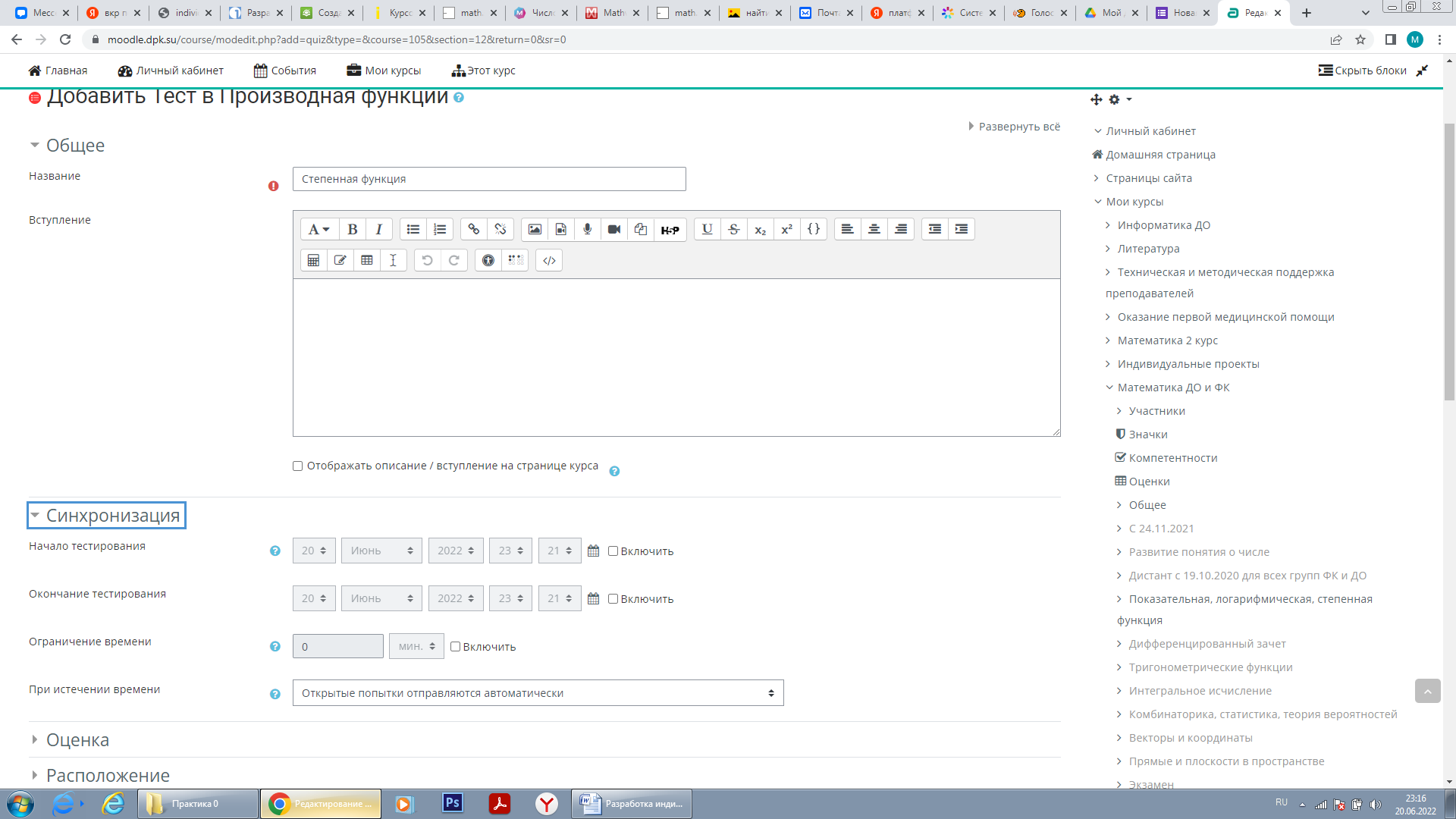
Рисунок 2. «Создания тестов на платформе Moodle»
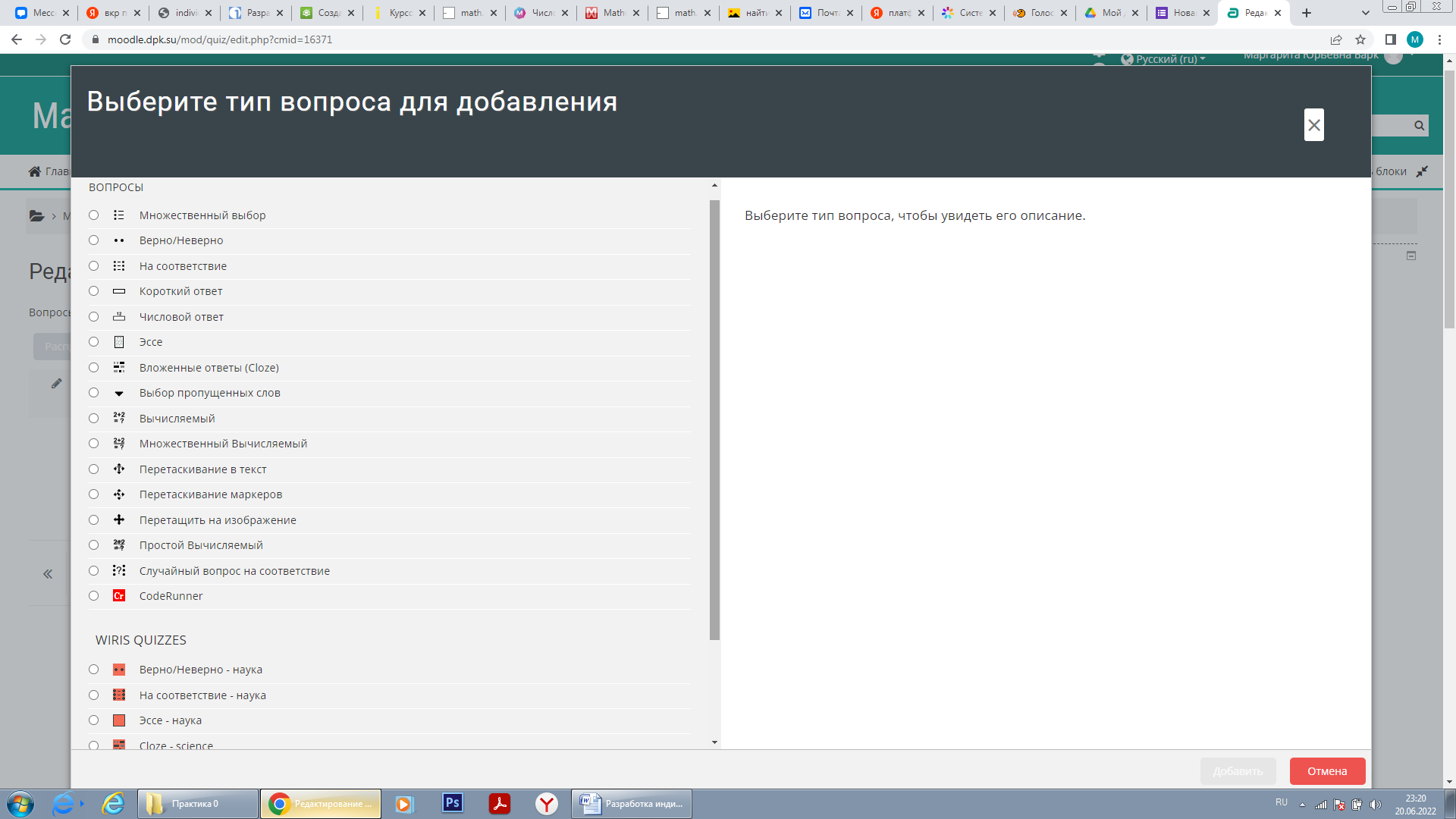
Рисунок 3. «Выбор вопросов теста»
У сервиса существует мобильное приложение, которое позволяет удобно проходить курсы и решать тесты с планшета или смартфона. Что является неотъемлемым плюсом для студентов-спортсменов.
Платформа позволяет студентам отслеживать успеваемость и составлять отчеты для преподавателей, то есть сколько времени обучающийся потратил время на прохождения курса, какие ошибки допустили в тесте, сколько времени он затратил на конкретный этап обучения.
Следующим этапом в разработке индивидуального образовательного маршрута является подготовка и разработка лекций. Учитывая, что у студентов-спортсменов не так много свободного времени на изучения материала, необходимо кратко описать теорию. В системе moodle предусмотрен ввод математических формул, но учитывая, что у некоторых студентов бывают проблемы с отображением данных через телефон, то лучше всего лекции набрать либо в формате word, либо pdf и оставить обучающимся возможность его скачать.
Рисунок 4. «Редактор формул в системе Moodle»
Рассмотрим создания индивидуального образовательного маршрута на примере темы «Производная функции», которая содержит следующий учебный материал:
Лекции: «Производная» (1 час), «Производная степенной функции» (1 час), «Правила дифференцирования» (1 час), «Производные некоторых элементарных функций. Геометрический смысл производной» (1 час).
Практическое занятие: «Дифференцирование степенной функции» (1 час), «Дифференцирование некоторых элементарных функций» (1 час), «Составление уравнения касательной к графику функции» (1 час).
Контрольная работа (1 час).
Самостоятельная работа обучающихся: подготовка сообщений по теме «Вклад ученых-математиков в развитие дифференциального исчисления» (1 час), вычисление производной сложной функции (2 часа).
Распишем все необходимые формулы и примеры решений по производным. Для этого будем использовать Microsoft Word, а именно панель для работы с математическими формулами.
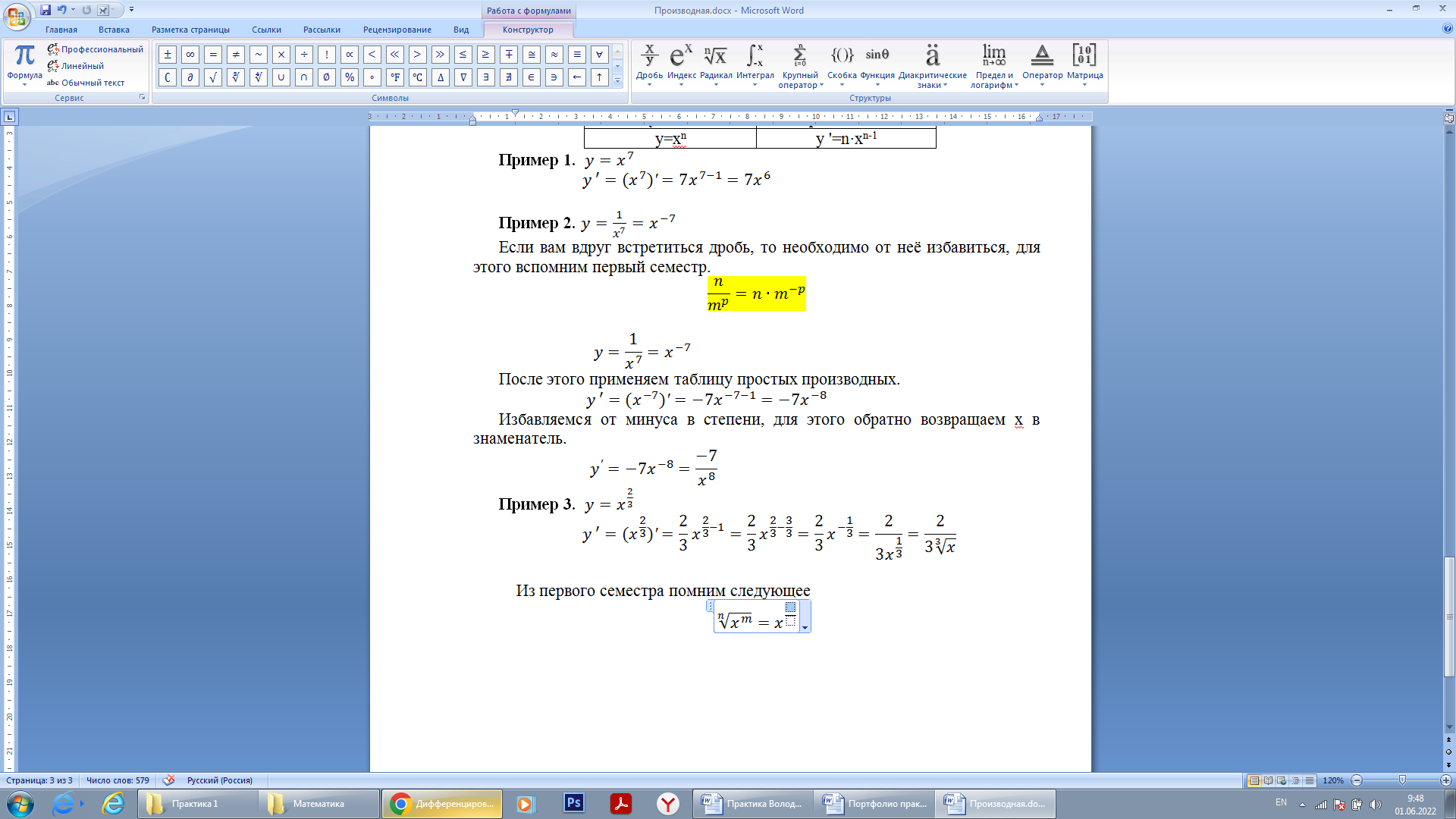
Рисунок 13. MicrosoftWord. Панель для работы с математическими формулами

Рисунок 5. MicrosoftWord. Лекция по теме «Производная степенной функции»
Следующим шагом сохраняем или конвертируем документ с разрешением docx в pdf или jpg. Делается это для того, чтобы обучающийся мог открыть документ на телефоне, так как формат docx поддерживается не на всех устройствах.
После этого на образовательном портале выкладываем лекцию. Если есть необходимость, то данный урок можно скрыть от студентов.
Рисунок 6. MicrosoftWord. Лекция по теме «Производная степенной функции»
Рисунок 7. Образовательный портал. Лекция по теме «Производная»
Дополнительно к лекциям добавим видео урок, для этого нам необходимо подобрать видео скопировать ссылку и просто вставить на основную страницу или же записать самостоятельно видео и загрузить его на страницу.
Рисунок 8. Образовательный портал. Лекция по теме «Производная»
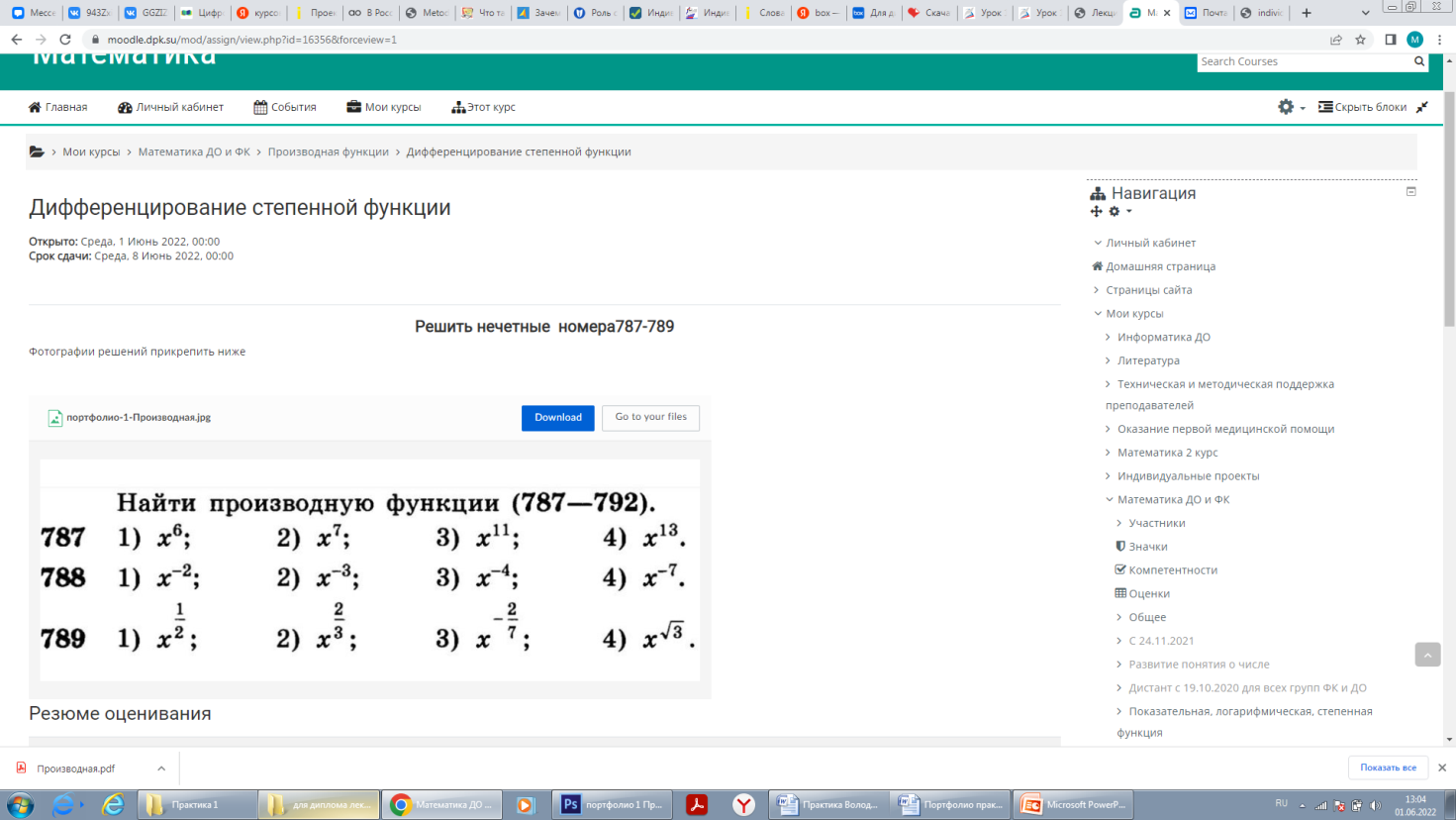
Рисунок 9. Образовательный портал. Домашнее задание по теме «Производная степенной функции»
Аналогично поступим и с практической частью. Для создания заданий порешению производной степенной функции используем математические формулы. С учётом того, что студент на примере простой степенной функции будет учиться находить производную, разделим задания на уровни:
Простой уровень:
Уровень 1: Найти производную степенной функции вида 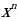
1) 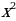 2)
2) 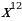 3)
3) 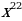
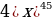
5) 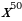 6)
6) 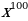 7)
7) 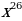
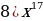
9) 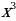 10)
10) 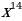 11)
11) 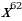
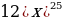
13) 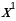 14)
14) 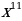 15)
15) 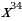
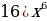
17) 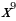 18)
18) 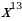 19)
19) 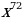
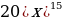
21) 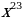 22)
22) 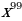 23)
23) 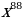
Уровень 2: Найти производную степенной функции вида 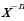
1) 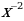 2)
2) 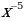 3)
3) 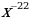
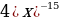
5) 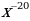 6)
6) 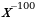 7)
7) 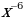
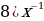
9) 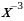 10)
10) 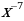 11)
11) 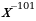
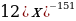
13) 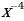 14)
14) 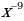 15)
15) 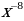
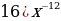
Уровень 3: Найти производную степенной функции вида 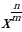
1) 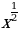 2)
2) 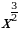 3)
3) 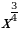
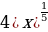
5) 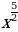 6)
6) 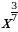 7)
7) 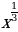
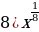
9) 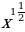 10)
10) 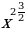 11)
11) 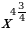
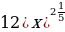
13) 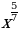 14)
14) 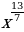 15)
15) 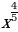
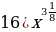
Уровень 4: Найти производную степенной функции вида 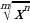
1) 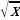 2)
2) 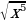 3)
3)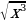 4)
4)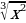
5) 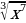 6)
6) 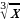 7)
7) 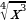
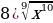
9) 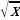 10)
10) 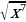 11)
11)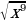 12)
12)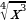
13) 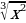 14)
14) 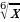 15)
15) 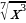
 16)
16) 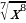

Средний уровень:
Уровень 1: Найти производную степенной функции вида 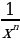
1) 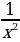 2)
2) 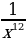 3)
3) 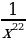 4)
4) 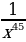
5) 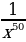 6)
6) 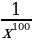 7)
7) 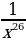
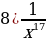
9) 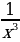 10)
10) 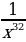 11)
11) 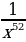 12)
12) 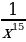
13) 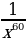 14)
14) 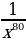 15)
15) 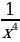
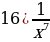
17) 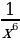 18)
18) 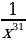 19)
19) 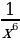 20)
20) 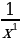
21) 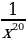 22)
22) 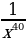 23)
23) 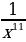
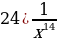
Уровень 2: Найти производную степенной функции вида 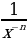
1) 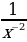 2)
2) 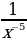 3)
3) 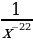 4)
4) 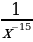
5) 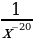 6)
6) 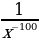 7)
7) 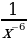
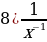
1) 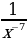 2)
2) 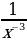 3)
3) 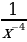 4)
4) 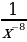
1) 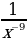 2)
2) 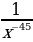 3)
3) 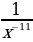 4)
4) 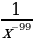
Уровень 3: Найти производную степенной функции вида 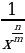
1) 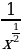 2)
2) 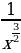 3)
3) 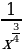 4)
4) 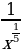
5) 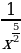 6)
6) 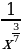 7)
7) 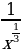
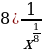
Сложный уровень:
Уровень 4: Найти производную степенной функции вида 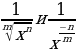
1) 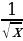 2)
2) 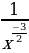 3)
3)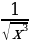 4)
4)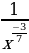
5) 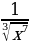 6)
6) 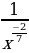 7)
7) 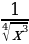
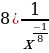
1) 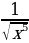 2)
2) 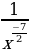 3)
3)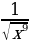 4)
4)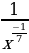
5) 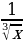 6)
6) 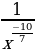 7)
7) 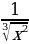
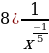
Деление примеров на такие уровни поможет студентам идти от самых простых вычислений к относительно сложным. При этом правила нахождение степенной функции отработается до автоматизма.
Рассмотрим практические задания по теме «Дифференцирование некоторых элементарных функций». Так как в этой теме применяются правила дифференцирования, которые создают сложности для большинства студентов-спортсменов, используем следующие уровни деления примеров:
Простой уровень:
1) 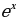 2) sinx 3) cosx 4) lnx 5)
2) sinx 3) cosx 4) lnx 5) 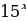 6)
6) 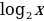 7) tgx 8) arcsinx
7) tgx 8) arcsinx
Средний уровень:
Правила сложения и вычитания
1) 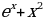 2)
2) 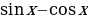 3)
3) 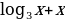 4)
4) 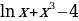
5) 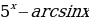 6)
6) 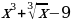 7)
7) 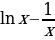 8)
8) 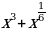
9) 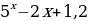 10)
10) 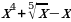 11)
11) 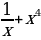 12)
12) 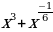
Правила умножения на частное
1) 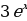 2) 4sinx 3) 5cosx
2) 4sinx 3) 5cosx
4) 7lnx 5) 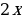 6)
6) 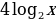
7) 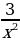 8)
8) 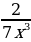 9) 2
9) 2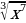
10) 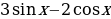 11)
11) 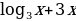
12) 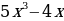 13)
13) 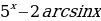 14)
14) 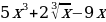
15) 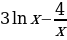 16)
16) 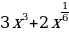 17)
17) 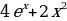
Правила умножения
1) 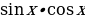 2)
2)  3)
3) 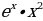
4) 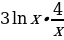 5)
5) 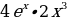 4)
4) 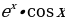
Правила деления
1) 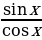 2)
2) 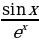 3)
3) 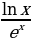
4) 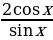 5)
5) 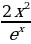 6)
6) 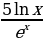
Сложный уровень:
Правила умножения
1)  2)
2) 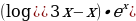 3)
3) 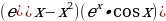
4) 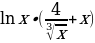 5)
5) 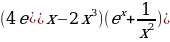
Правила деления
1) 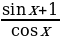 2)
2) 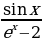 3)
3) 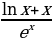
4) 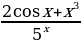 5)
5) 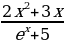 6)
6) 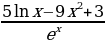
Для подготовки к контрольной работе студенту предлагается еще раз вспомнить, как находить производную и правила дифференцирования.
|
| Простые производные решать с помощью xn |
| 1 | 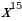
| 3 | 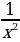
|
| 2 | 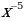
| 4 | 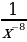
|
| 5 | 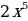 (правило умножение на константу) (правило умножение на константу)
| 7 | 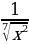
|
| 6 | 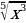 | 8 | 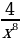 (правило умножение на константу) (правило умножение на константу)
|
| Правила дифференцирования (+ и -) |
| 9 | cosx+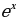 | 11 | 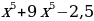
|
| 10 | 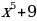
| 12 | 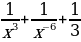
|
| Правила дифференцирования (умножение) |
| 13 | 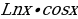
| 15 | (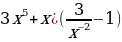 |
| 14 | 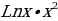
| 16 | 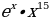
|
| Правила дифференцирования (деление) |
| 17 | 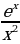
| 19 | 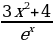
|
| 18 | 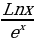
| 20 | 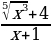
|
| Сложные производные |
| 21 | 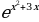
| 23 | 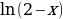
|
| 22 | 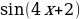
| 24 | 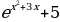
|
| 25 | 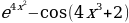
| 27 | 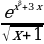
|
| 26 | 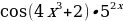
| 28 | 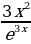
|
Контрольная работа разработана в нескольких вариантах, один из вариантов будет случайным образом открываться у обучающегося. Его задачей будет решить задания на листочке и пока время не вышло прикрепить ответ в виде файла в отведенном для этого месте.
Контрольная работа по теме «Производная функции»
Вариант 1.
1.Найти производную функции:
a) 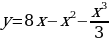
b) 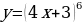
c) 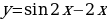
d)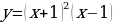
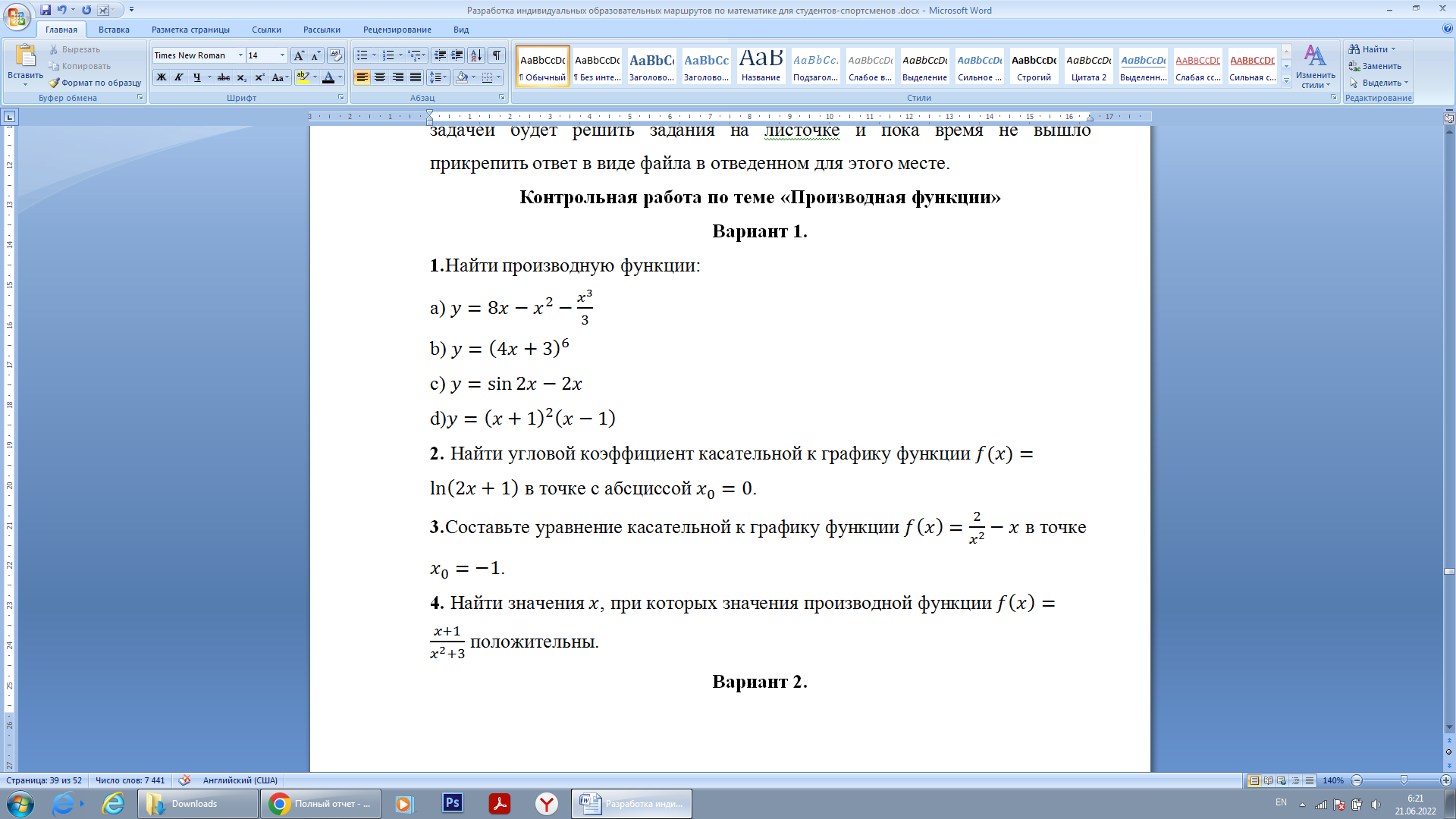
Вариант 2.
1.Найти производную функции:
a) 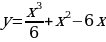
b) 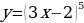
c) 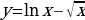
d)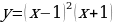
Вариант 3.
1.Найти производную функции:
a) 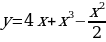
b) 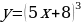
c) 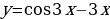
d)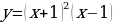
Вариант 4.
1.Найти производную функции:
a) 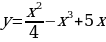
b) 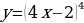
c) 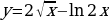
d)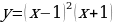
Такая организация образовательного обучения даст возможность первокурсникам не только защищать честь колледжа, но и не отставать в обучение от сверстников. Так же многообразия возможностей образовательной платформы позволит преподавателям меньше тратить времени на организацию и проверку индивидуального образовательного маршрута, и поможет заинтересовать студентов в выполнении заданий.















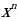
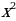 2)
2) 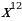 3)
3) 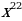
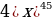
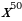 6)
6) 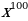 7)
7) 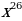
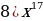
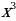 10)
10) 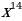 11)
11) 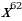
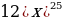
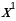 14)
14) 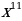 15)
15) 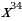
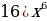
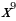 18)
18) 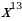 19)
19) 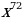
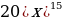
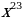 22)
22) 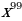 23)
23) 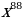
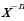
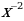 2)
2) 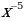 3)
3) 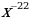
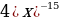
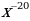 6)
6) 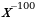 7)
7) 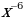
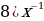
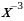 10)
10) 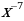 11)
11) 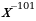
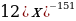
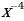 14)
14) 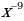 15)
15) 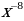
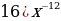
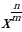
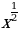 2)
2) 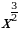 3)
3) 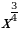
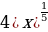
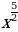 6)
6) 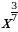 7)
7) 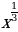
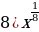
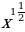 10)
10) 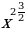 11)
11) 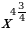
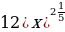
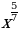 14)
14) 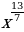 15)
15) 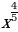
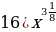
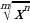
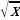 2)
2) 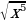 3)
3)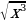 4)
4)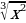
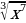 6)
6) 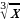 7)
7) 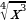
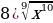
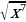 11)
11)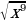 12)
12)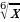 15)
15) 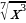
 16)
16) 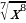
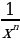
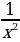 2)
2) 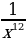 3)
3) 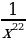 4)
4) 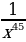
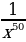 6)
6) 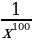 7)
7) 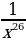
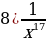
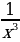 10)
10) 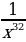 11)
11) 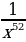 12)
12) 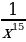
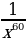 14)
14) 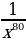 15)
15) 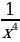
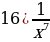
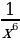 18)
18) 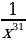 19)
19) 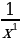
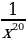 22)
22) 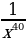 23)
23) 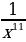
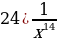
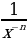
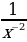 2)
2) 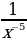 3)
3) 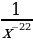 4)
4) 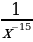
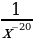 6)
6) 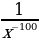 7)
7) 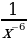
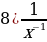
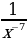 2)
2) 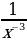 3)
3) 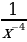 4)
4) 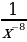
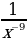 2)
2) 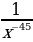 3)
3) 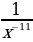 4)
4) 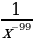
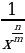
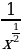 2)
2) 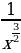 3)
3) 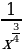 4)
4) 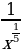
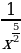 6)
6) 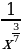 7)
7) 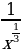
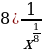
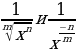
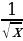 2)
2) 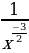 3)
3)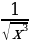 4)
4)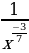
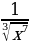 6)
6) 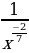 7)
7) 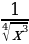
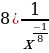
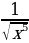 2)
2) 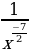 3)
3)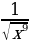 4)
4)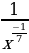
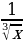 6)
6) 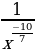 7)
7) 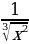
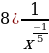
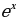 2) sinx 3) cosx 4) lnx 5)
2) sinx 3) cosx 4) lnx 5) 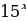 6)
6) 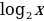 7) tgx 8) arcsinx
7) tgx 8) arcsinx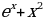 2)
2) 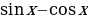 3)
3) 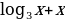 4)
4) 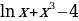
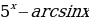 6)
6) 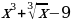 7)
7) 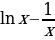 8)
8) 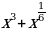
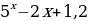 10)
10) 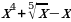 11)
11) 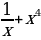 12)
12) 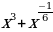
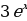 2) 4sinx 3) 5cosx
2) 4sinx 3) 5cosx 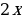 6)
6) 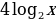
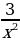 8)
8) 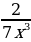 9) 2
9) 2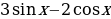 11)
11) 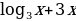
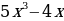 13)
13) 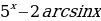 14)
14) 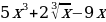
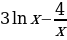 16)
16) 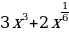 17)
17) 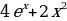
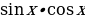 2)
2) 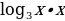 3)
3) 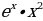
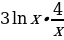 5)
5) 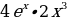 4)
4) 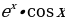
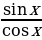 2)
2) 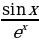 3)
3) 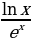
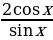 5)
5) 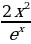 6)
6) 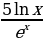
 2)
2) 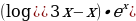 3)
3) 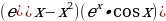
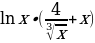 5)
5) 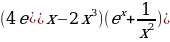
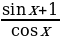 2)
2) 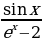 3)
3) 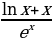
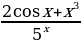 5)
5) 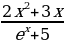 6)
6) 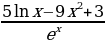
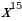
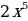 (правило умножение на константу)
(правило умножение на константу)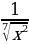
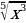
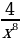 (правило умножение на константу)
(правило умножение на константу)