ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«Мордовский государственный
педагогический УНИВЕРСИТЕТ имени М. Е. евсевьева»
Физико-математический факультет
Кафедра информатики и вычислительной техники
РЕФЕРАТ
3D ПОСТРОЕНИЯ В СИСТЕМЕ SCILAB
| Автор работы____________________________________ М. Г. Ейкина Направление подготовки 44.03.05 Педагогическое образование Профиль Математика. Информатика
|
|
Руководитель работы канд. физ.-мат. наук, доцент___________________________Т. В. Кормилицына |
Оценка ____________________
Саранск 2020
Содержание
Общая характеристика системы Scilab.......................................................3
Построение графиков трехмерных поверхностей ……….………………5
Функции plot3d и plot3d1…………………………………………………..5
Функции meshgrid, surf и mesh……………………………………………8
Функции plot3d2 и plot3d3………………………………………………..11
Список использованных источников……………………………………16
Общая характеристика системы Scilab
Scilab – это кроссплатформенная система компьютерной математики (СКМ), которая предназначена для выполнения научно-технических расчетов, графической интерпретации полученных результатов и визуального моделирования. Эта система имеет удобный пользовательский интерфейс и развитый язык программирования.
Scilab свободно распространяется центром Scilab Consortium, с Web-узла www.scilab.org [7], с которого можно загрузить последнюю версию программы и комплект документации.
Разработка системы Scilab ведется сотрудниками французского Национального института информатики и автоматизации (INRIA – Institut National de Recherche en Informatique et Automatique) с 80-х годов прошлого века. Изначально это был коммерческий проект под названием Blaise, а затем Basile. С 2003 года продукт получил новое имя Scilab и стал бесплатным. Для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция). В настоящее время он распространяется по свободной лицензии CeCILL.
Сама система Scilab, как и Matlab, предназначена прежде всего для численных расчетов и работы с матрицами. Кроме того, она обладает развитыми средствами программирования, так что ее в какой-то мере можно рассматривать как систему разработки высокотехнологичных приложений.
Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.
Все возможности системы можно классифицировать так:
- математические;
- использования численных методов;
- программирование;
- графические;
- имитационное моделирование;
- сервисные.
Математические возможности перечислены ниже.
- Вычисление арифметических и логических выражений.
- Вычисление стандартных математических функций.
- Операции с векторами и матрицами.
- Матричные операции линейной алгебры
и т.д.
Система имеет несколько режимов работы, каждый из которых поддерживается собственным диалоговым окном (рис.1).
- Командный режим – командное окно.
- Программный режим – окно создания и редактирования программных файлов (SCE-файлов).
- Графический режим – окно редактирования графиков.
- Режим помощи – окно помощи.
- Режим демонстрации – окон демонстрационных примеров.

Рис.1. Режимы работы Scilab
При работе в любом из перечисленных режимов могут быть использованы дополнительные информационные окна.
Окно рабочей области (Обозреватель переменных) – предназначено для просмотра и редактирования содержимого рабочей области памяти, в нем указывается имя переменной (массива или структуры), ее размерность и тип.
Окно журнала команд содержит перечень команд, введенных пользователем в командном режиме за текущий и предыдущий сеансы работы с системой.
Окно управления файлами (обозреватель файлов) служит для быстрого доступа к файлам при работе с системой.
Управлять информационными окнами можно с использованием пункта основного меню «Инструменты».
Построение графиков трехмерных поверхностей
Процесс построения графика функции вида Z(x, y) можно разделить на три этапа:
1. Создание в области построения графика прямоугольной сетки. Для этого формируются прямые линии, параллельные координатным осям xi и yj , где

2. Вычисление значений функции zij = f(xi, yj) во всех узлах сетки.
3. Обращение к функции построения трехмерных графиков.
Функции plot3d и plot3d1
В Scilab поверхность можно построить с помощью функций plot3d или plot3d1. Их отличие состоит в том, что plot3d строит поверхность и заливает ее одним цветом, а plot3d1 - поверхность, каждая ячейка которой имеет цвет, зависящий от значения функции в каждом соответствующем узле сетки.
Обращение к функциям следующее:
plot3d(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),
plot3d1(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),
здесь x - вектор-столбец значений абсцисс;
y - вектор-столбец значений ординат;
z - матрица значений функции;
theta, alpha - действительные числа, которые определяют в градусах сферические координаты угла зрения на график. Или это угол, под которым наблюдатель видит отображаемую поверхность;
leg - подписи координатных осей графика - символы, отделяемые знаком @. Например, ’X@Y@Z’.
flag - массив, состоящий из трех целочисленных параметров: [mode,type,box].
Здесь mode - устанавливает цвет поверхности (см. табл.). По умолчанию равен 2- цвет заливки синий, прямоугольная сетка выводится.
Таблица. Значения параметра mode
| Значение | Описание |
| 0 | поверхность имеет цвет «mode», выводится прямоугольная сетка |
| 0 | выводится прямоугольная сетка, заливка отсутствует (белый цвет) |
| 0 | поверхность имеет цвет «mode», отсутствует прямоугольная сетка |
type - позволяет управлять масштабом графика (см. табл.), по умолчанию имеет значение 2;
Таблица. Значения параметра type
| Значение | Описание |
| 0 | применяется способ масштабирования, как у ранее созданного графика |
| 1 | границы графика указываются вручную с помощью параметра ebox |
| 2 | границы графика определяют исходные данные |
box - определяет наличие рамки вокруг отображаемого графика (см. табл.). По умолчанию равен 4.
Таблица. Значения параметра box
| Значение | Описание |
| 0 и 1 | Нет рамки |
| 2 | только оси, находящиеся за поверхностью |
| 3 | выводится рамка и подписи осей |
| 4 | выводится рамка, оси и их подписи |
ebox - определяет границы области, в которую будет выводиться поверхность, как вектор [xmin, xmax, ymin, ymax, zmin, zmax].
Этот параметр может использоваться только при значении параметра type=1.
keyn=valuen - последовательность значений свойств графика key1=value1, key2=value2, ..., keyn=valuen, таких как толщина линии, ее цвет, цвет заливки фона графического окна, наличие маркера и др. (как для двумерного).
Таким образом, функции plot3d (plot3d1) в качестве параметров необходимо передать прямоугольную сетку и матрицу значений в узлах сетки.
Задача 1. Построить график функции Z = sin(t) · cos(t).
Создадим массив значений аргумента t. Вычислим значения функции и запишем их в массив Z.
При обращении к функции plot3d в качестве параметров X и Y , задающих прямоугольную сетку, дважды указан параметр t, поскольку обе функции - и sin, и cos - зависят от одной переменной - t.
Листинг 1. Построение графика функции Z = sin(t) · cos(t) с помощью функции plot3d
t=[0:0.3:2*%pi]';
z=sin(t)*cos(t');
plot3d(t,t,z)
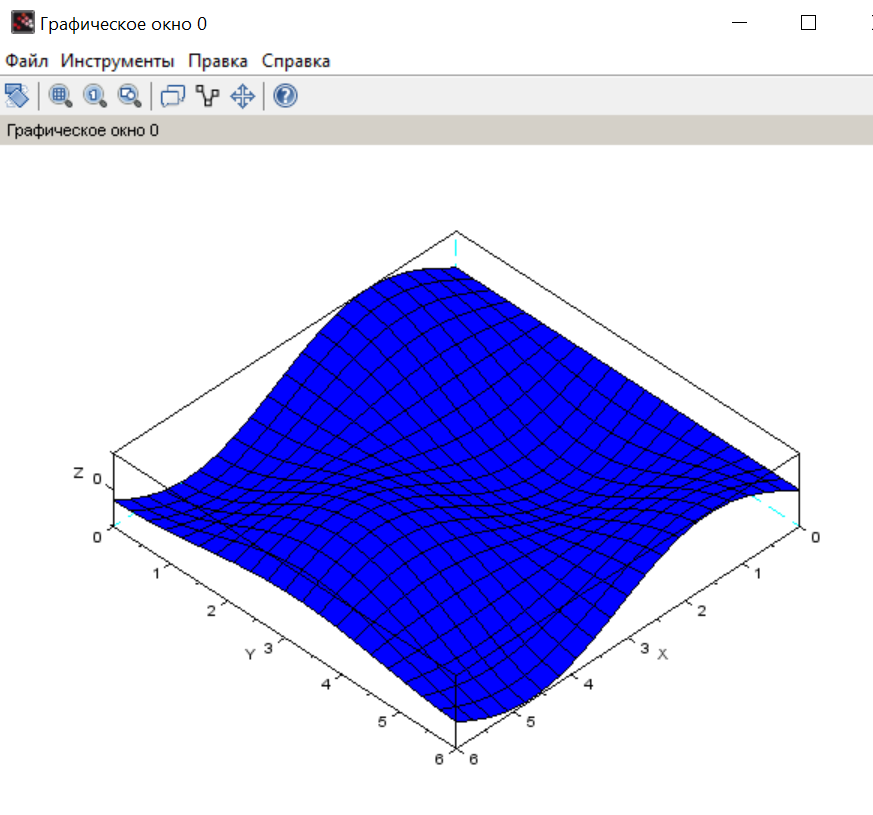
Рис.2 График функции z=sin(t)cos(t)
Функции meshgrid, surf и mesh
Для формирования прямоугольной сетки используется функция meshgrid. Обращение к ней имеет вид:
[X, Y [Z]] = meshgrid(x, y [z])
здесь (x, y [z]) - массивы 2 (3) исходных параметров X, Y (Z), указываемые через запятую;
[X, Y [Z]] - матрицы в случае 2 и массивы в случае 3 входных величин.
После формирования сетки вывести в нее график можно с помощью функции surf либо mesh. Так же, как и в случае с функциями plot3d и plot3d1, surf строит поверхность, заливая каждую ячейку цветом, который зависит от конкретного значения функции в узле сетки, а mesh заливает ее одним цветом (рис.3).
Пример.
[x, y] = meshgrid([3:0.15:3]);
Z = х.^2+у.^2;
plot3d(x, y, z);
Задается опорная плоскость для построения трехмерной поверхности, переменные x, y меняются от –3 до 3 с шагом 0,15.
Результат работы программы представлен на рис. 3.
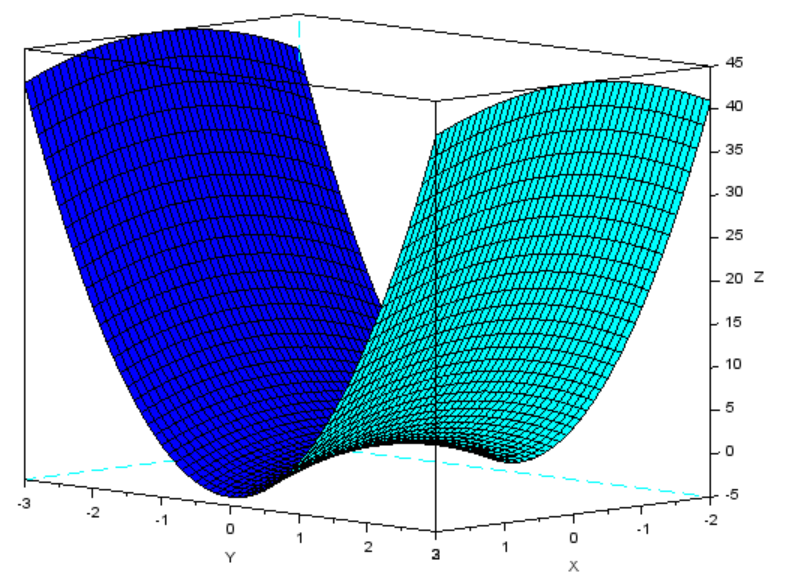
Рис. 3 График функции z=x2+y2
Рассмотрим примеры использования функций mesh и surf.
Пример 1.
scf;
[х,у]=meshgrid(2:0.2:2,3:2:3);
z=х.^2+y*sin(x);
mesh(x,у,z);
Результат выполнения операторов изображен на рис. 4.

Рис. 4 График функции z = х2 + ysin(x), построенный функцией mesh
Пример 2.
scf;
[х, у]=meshgrid(2:0.2:2, 3:.2:3);
z=х.^2+у.*sin(x);
surf(x,у,z)
Результат выполнения операторов изображен на рис. 5.

Рис. 5 График функции z=х2 +ysin(x), построенный функцией surf
Таким образом, mesh является полным аналогом функции surf со значением параметров Сolor mode=индекс белого цвета в текущей палитре цветов и Сolor flag=0.
Обращение к функциям имеет вид:
surf([X,Y],Z,[color,keyn=valuen])
mesh([X,Y],Z,[color,])
здесь X,Y - массивы, задающие прямоугольную сетку;
Z _матрица значений функции;
color - матрица действительных чисел, устанавливающих цвет для каждого узла сети;
keyn=valuen - последовательность значений свойств графика key1=value1, key2=value2, ..., keyn=valuen, определяющих его внешний вид.
Функции plot3d2 и plot3d3
Функции plot3d2 и plot3d3 являются аналогами функции plot3d, поэтому имеют такой же синтаксис:
plot3d2(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),
plot3d3(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen])
Эти функции предназначены для построения поверхности, которая задается набором граней. Т. е. если функция plot3d по входным данным сможет построить лишь отдельно стоящие друг от друга плоские грани, то plot3d2 (plot3d3) проинтерпретирует взаимное расположение этих граней в виде цельного геометрического тела.
Отличие функций plot3d2 и plot3d3 сходно с различием действия функций plot3d и plot3d1, а также surf и mesh. Plot3d2 строит поверхность, при этом выводит сетку и заливает все ячейки одним из цветов, по умолчанию – синим. Plot3d также выводит сетку, однако оставляет все ячейки без заливки (т. е. белыми).
Пример 3. Построить сферу при помощи функции plot3d2.

При построении графиков поверхностей, заданных параметрически - x(u, v), y(u, v) и z(u, v) - необходимо сформировать матрицы X, Y и Z одинакового размера. Для этого массивы u и v должны иметь одинаковый размер.
После этого следует выделить два основных вида представления x, y и z в случае параметрического задания поверхностей:
1. Если x, y и z можно представить в виде f(u) · g(v), то соответствующие им матрицы X, Y и Z следует формировать в виде матричного умножения f(u) на g(v).
2. Если x, y и z можно представит в виде f(u) или g(v), то в этом случае матрицы X, Y и Z следует записывать в виде f(u) · ones(size(v)) или g(v) · ones(size(u)) соответственно.
Здесь linspace - функция, возвращающая массив с линейным приращением значений в заданном диапазоне. Например, u=linspace(-%pi/2,%pi/2,40) значит, что параметр u линейно изменяется в диапазоне [−2π; 2π]. Число 40 устанавливает, что массив должен содержать ровно 40 значений, по умолчанию их 100.
Построение сферы с помощью функции plot3d2
u = linspace(-%pi/2,%pi/2,40);
v = linspace(0,2*%pi,20);
X = cos(u)'*cos(v);
Y = cos(u)'*sin(v);
Z = sin(u)'*ones(v);
plot3d2(X,Y,Z);
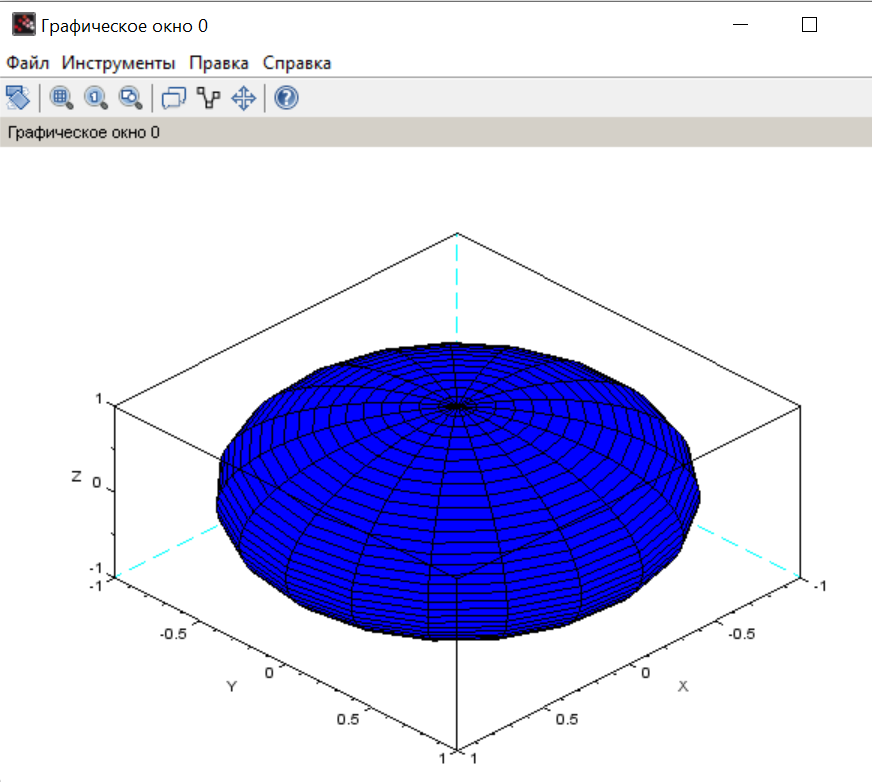
Пример 4. Построить сферу при помощи функции plot3d.

u = linspace(-%pi/2,%pi/2,40);
v = linspace(0,2*%pi,20);
X = cos(u)'*cos(v);
Y = cos(u)'*sin(v);
Z = sin(u)'*ones(v);
plot3d2(X,Y,Z);
e=gce();
e.color_mode=4; // change color
f=e.data;
TL = tlist(["3d" "x" "y" "z" "color"],f.x,f.y,f.z,10*(f.z)+1);
e.data=TL;
e.color_flag=2;

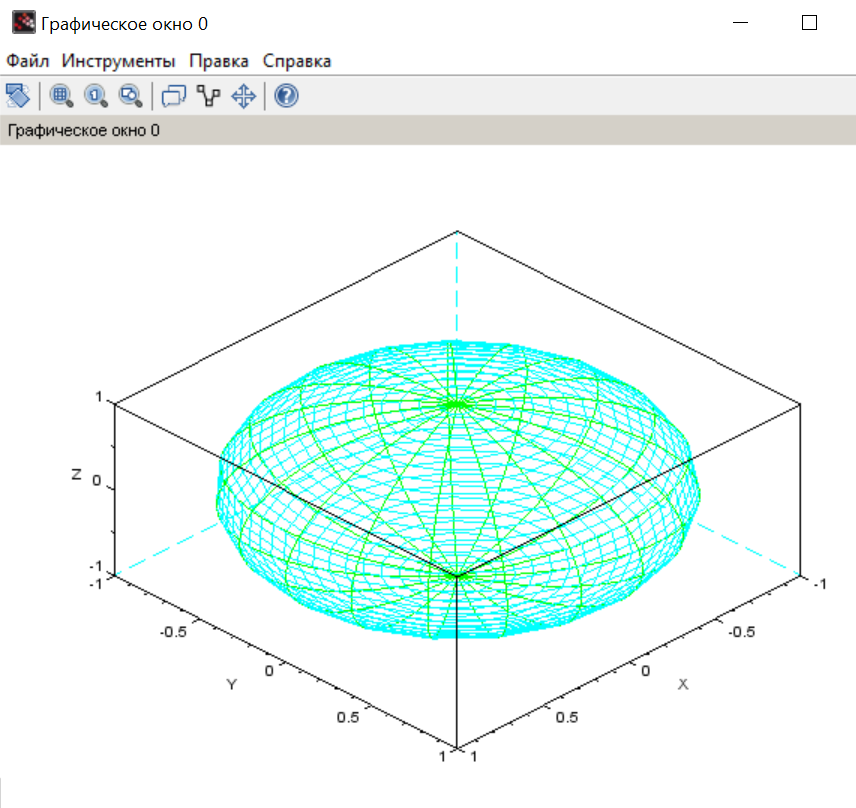
Пример 5. Построить сферу при помощи функции plot3d3.

u = linspace(-%pi/2,%pi/2,20);
v = linspace(0,2*%pi,20);
X = cos(u)’*cos(v);
Y = cos(u)’*sin(v);
Z = sin(u)’*ones(v);
plot3d3(X,Y,Z);
Список использованных источников
Алексеев, Е. Р. Авторский курс лекций по пакету Scilab на странице Е. Р. Алексеева. – Текст : электронный // Личный сайт Е. Р. Алексеева – Работа в пакете Scilab. – URL : https://teacher.ucoz.net/index/rabota_v_pakete_scilab/0-9
Алексеев, Е.Р. Scilab: решение инженерных и математических задач / Е. Р. Алексеев, О. В. Чеснокова, Е. Р. Рудченко. – Москва: ALT Linux; БИНОМ. Лаборатория знаний, 2008. 260 с.
Андриевский, Б. Элементы математического моделирования в программных средах MATLAB 5 и Scilab / Б. Андриевский, А. Фрадков. – Санкт-Петербург: Наука, 2001. - 286 с.
Интегрированные системы компьютерной математики : учебное пособие для бакалавров / Т. В. Кормилицына, М. А. Кокорева ; Мордовский государственный педагогический институт. – Саранск, 2014. – 197 с.
Интерактивная система Scilab: учебное пособие. / И. Е. Плещинская, А. Н. Титов. - Казань: КГТУ, 2009. 144 с.
Интерактивные системы Scilab, Matlab, Mathcad : учебное пособие / И. Е. Плещинская [и др.]. – Текст: электронный // Министерство образования и науки России, Казанский национальный исследовательский технологический университет – Казань : Издательство КНИТУ, 2014. - 195 с. ISBN 978-5-7882-1715-4. – URL : // biblioclub.ru/index.php?page=book&id=428781
Ссылка на скачивание. – Текст : электронный // Официальный сайт Scilab. – URL : http://www.scilab.org/
14


























