Решение арифметических задач с помощью кругов Эйлера.

Муниципальное бюджетное образовательное учреждение «Детский сад № 45 «Октябрёнок» города Смоленска

Презентация

Тема: «Решение арифметических задач с помощью кругов Эйлера»

Подготовила: Апраксина Г.В.-

старший воспитатель

Смоленск, 2023

В соответствии с ФГОС ДО основным принципом дошкольного образования является формирование познавательных интересов и познавательных действий ребёнка в различных видах деятельности, а также развитие интеллектуальных качеств дошкольников. Следуя современным тенденциям развития образования, мы должны выпустить из детского сада, ребёнка любознательного, интересующегося причинно-следственными связями, активного, умеющего наблюдать и экспериментировать, рассуждать и строить умозаключения, обладающего способностью решать интеллектуальные задачи, принимать собственные решения .

Психолог П. Симонов справедливо указывал, что если интуиции бывает достаточно для усмотрения истины, то ее недостаточно, чтобы убедить в этой истине других. Для этого нужны доказательства. Поиск этих доказательств осуществляется с помощью логического мышления. Комплексная программа «Развитие» определяет образовательное содержание по всем направлениям работы с обучающими в условиях детского сада на основе единой педагогической концепции. Особое место занимает ознакомление с логическими отношениями - с помощью специальных приемов и средств (картинок, схем, кругов) обучающиеся узнают о простейших логических операциях.

Данная программа дает нам возможность использовать скрытые резервы умственной деятельности детей, поиск путей эффективного обучения. Наглядное моделирование - это наиболее универсальное средство, которое соответствует специфике наглядно-образного мышления детей. Метод помогает ребенку зрительно представить абстрактные понятия и научиться работать с ними. Позволяет предотвратить быструю утомляемость, создать интерес к образовательной деятельности, а главное видеть главное, систематизировать полученные знания.

Логическое мышление

Наглядно-образное мышление

Способность «действовать в уме»

Дети очень быстро и легко

понимают разного

рода схематические

изображения и с успехом

пользуются ими.

Эффективность развития

логического мышления дошкольников возрастает, если в качестве средств обучения выступают наглядные модели в форме кругов Эйлера или сериационного ряда классификационного древа. В процессе развивающей работы воспитателю не надо стремиться детям все объяснять, а надо лишь направлять на путь поиска, давать им возможность самим искать и находить варианты ответов.

Задача педагога

• В старшей группе : освоение действий моделирования отношений между числами числового ряда при помощи модели «Круги Эйлера».

• В подготовительной группе:

овладение действиями

сравнения чисел с заданным

числом, пользуясь моделями:

• «Круги Эйлера»
• «Логическое древо».

Что же представляют собой круги Эйлера

Круги Эйлера – это геометрическая схема, благодаря которой можно наглядно отобразить отношения между понятиями или множествами объектов, цифр и фигур.  

Круги Эйлера были изобретены математиком, физиком

и астрономом Леонардом

Эйлером в 18 веке и с тех пор

широко используются в

математике, логике и

в различных прикладных направлениях.

Круги Эйлера - очень интересный способ развития математического и логического мышления детей дошкольного возраста. При решении многих задач метод Эйлера просто незаменим и значительно упрощает рассуждение. «Круги очень подходят для того, чтобы облегчить наши размышления» говорил Л.Эйлер. Модели кругов Эйлера – просты и наглядны, поэтому они с большим успехом используются для математического развития детей дошкольного возраста.

Если ребенок научится строить модели, отражающие обобщенные, существенные черты множеств объектов, он получит в свои руки инструмент, с помощью которого в дальнейшем сумеет познавать и конструировать действительность, а также самостоятельно анализировать те множества, которые перед ним. Именно поэтому в старших и подготовительных группах большое количество образовательных ситуаций посвящено действиям наглядного моделирования с помощью кругов Эйлера.

Имея опыт работы по развитию логического мышления в старшей группе наши воспитатели применяют круги Эйлера в решении математических задач в подготовительной к школе группе. Работа с детьми по развитию математических способностей

включается во все

основные структуры

педагогического процесса: - учебные занятия в форме

прямых образовательных

ситуаций; - организацию совместной

деятельности с детьми; - предоставление детям

возможности для свободной самостоятельной деятельности;

- наличие центра по познавательному развитию.

Для проведения образовательной деятельности с кругами Эйлера воспитатели используют игры-путешествия, видео - встречи со сказочными героями, мультимедийную технику, телевизор, интерактивную доску.

А сейчас мы Вам предлагаем варианты арифметических задач с кругами Эйлера, и числовой оси. Данные задачи педагоги составляют самостоятельно.

Задача 1

• Для 12 детей купили на елочном базаре деревья. Из них 7 елок, остальные сосны. Сколько купили сосен?

Ёлок - 7

Сосен - ?

0 1 2 3 4 5 6 7 8 9 10 11 12

• Воспитатель: Скажите чего больше сосен или елок? (елок)

?

Задача 2

• У нас с вами 7 елок и 5 сосен. Вопрос: На сколько елок больше чем сосен?
• Ответ: на 2 елки больше.

0 1 2 3 4 5 6 7 8 9 10 11 12

?

Задача 3

• Ребята, а давайте узнаем сколько елок можно купить на 12 рублей если одна ёлочка стоит четыре рубля.

0 1 2 3 4 5 6 7 8 9 10 11 12

Ответ: 3 елки

Задача 4

На праздник в детский сад заказали костюмы. Привезли 4 костюма снежинок и 5 костюмов гномов. Сколько всего костюмов привезли?

0 1 2 3 4 5 6 7 8 9 10 11 12

Ответ: 9 костюмов

Воспитатель: с помощью кругов Эйлера можно решать не только арифметические задачи, но и неравенства.

Задача 5

• Давайте расположим числа от 1 до 12 в кругах Эйлера по следующему правилу:

5  

9 10 11 12

1 2 3 4 5

6

7

8

Задача 6

На праздник пришло 12 детей. Под елкой лежат подарки . 4 подарка в пакетах и 8 в коробках. Давайте проверим хватает ли на всех подарков?

0 1 2 3 4 5 6 7 8 9 10 11 12

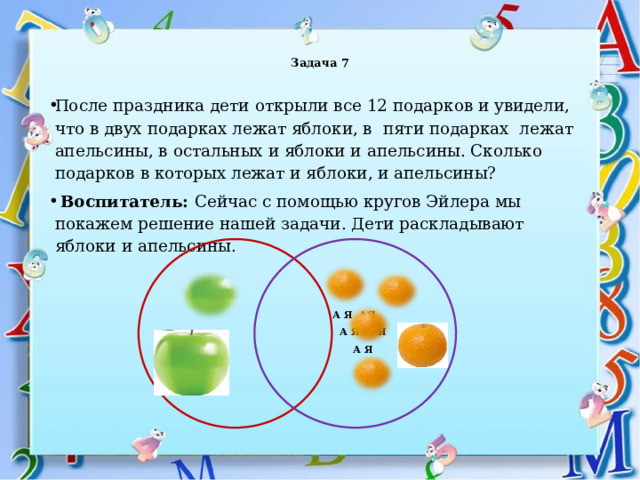
Задача 7

• После праздника дети открыли все 12 подарков и увидели, что в двух подарках лежат яблоки, в пяти подарках лежат апельсины, в остальных и яблоки и апельсины. Сколько подарков в которых лежат и яблоки, и апельсины?
• Воспитатель: Сейчас с помощью кругов Эйлера мы покажем решение нашей задачи. Дети раскладывают яблоки и апельсины.

А Я АЯ

А Я А Я

А Я

Вывод:

• Решая арифметические задачи при помощи кругов Эйлера мы наглядно представляем детям отношения между множествами. Они учатся строить довольно сложные модели с несколькими кругами, рассуждают и делают умозаключения. Из чего следует, что мы вооружаем детей необходимыми инструментами для дальнейшего успешного обучения в школе. Учиться станет легче и процесс учебы и школьная жизнь будут приносить ребенку радость и удовольствие.

• Литература:
• Программа «Развитие» Л.Венгера

УЦ им. Венгера «Развитие» Москва, 2002

• Планы занятий по программе «Развитие» для подготовительной группы. УЦ им. Венгера «Развитие» Москва, 2000
• Сборник практических материалов для ДОУ к программе «Развитие», АРКТИ Москва, 2007
• Интернет ресурсы.