Открытый урок алгебры в 8 классе по теме:
Решение дробно-рациональных уравнений.
Подготовила учитель математики Халявка Т.В.
2019г.
Тема: Решение дробно-рациональных уравнений.
Цель: познакомить с новым видом уравнений - дробными рациональными уравнениями, дать представление об алгоритме решения дробных рациональных уравнений.
Задачи:
Образовательные
Формирование умения и навыков решения дробных рациональных уравнений.
Применение ЗУН упрощения рациональных выражений.
Развивающие
Развитие умений выделять главное, существенное в изученном материале.
Формирование умений сравнивать, классифицировать, обобщать факты и понятия.
Формировать умение пользоваться алгоритмом.
Развитие у учащихся самостоятельности в мышлении и в учебной деятельности.
Развитие у учащихся познавательного интереса, внимания, математической зоркости.
Воспитательные
Содействовать формированию мировоззренческих понятий.
Воспитывать чувство коллективизма, сопереживания за группу, товарища.
Предметные УУД:
Формировать умения решать простейшие дробно-рациональные уравнения, находить область допустимых значений переменной.
Познавательные УУД:
умение анализировать примеры с целью выделения общих признаков, классифицировать по группам, самостоятельное выделение и формулирование познавательной задачи.
Регулятивные УУД: умение оценивать результат своих действий, контролировать самого себя, находить и исправлять свои ошибки.
Коммуникативные УУД: умение работать в группе, умение выражать свои мысли.
Формы работы учащихся: индивидуальная, фронтальная, групповая.
Образовательные технологии: технология деятельностного подхода, технология проблемного диалога, элементы технологии кроссенс
СЦЕНАРИЙ УРОКА
Организационный момент
Мотивация к учебной деятельности
Математическое лото
-На доске карточка игры ЛОТО. У вас на карточках записаны числовые выражения, а у меня части из фразы, которую я выбрала для девиза нашего урока. Каждая группа должна определить к какой паре дробей относится общий знаменатель и к какому выражению предложено ОДЗ.
| х2-9 Поверь в себя - | х(х-2) и ты всё | х(х-3) сможешь, |
| х≠-3 Иди | х≠0, х≠5 вперёд - | х≠1 и победишь! |
- Как понимаете эти слова?
-Поставьте в оценочном листе по 2 балла за правильный ответ.
Мини-кроссенс1
Прежде чем перейти к изучению нового материала, давайте проведем разминку для нашего мозга и решим первый мини-кроссенс, который нам подскажет, какие задания будем выполнять.
а,в,с


Франсуа Виет
х1,х2
Ответ:
ах2+вх+с=0, а≠0

-Поставьте в оценочном листе по 1 баллу за правильный ответ.
Французский ученый XVI в. Франсуа Виет первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин.
Фронтальный опрос (правильный ответ – 1 балл)
-Что называется квадратным уравнением?
-Как называются коэффициенты квадратного уравнения?
-Какое квадратное уравнение называется полным?
-Какие квадратные уравнения называются неполными?
-Какое квадратное уравнение называется приведенным?
-Какое неприведенным?
-Что называется корнями квадратного уравнения?
- Что значит решить квадратное уравнение?
- Вспомните алгоритмы решения квадратных уравнений.
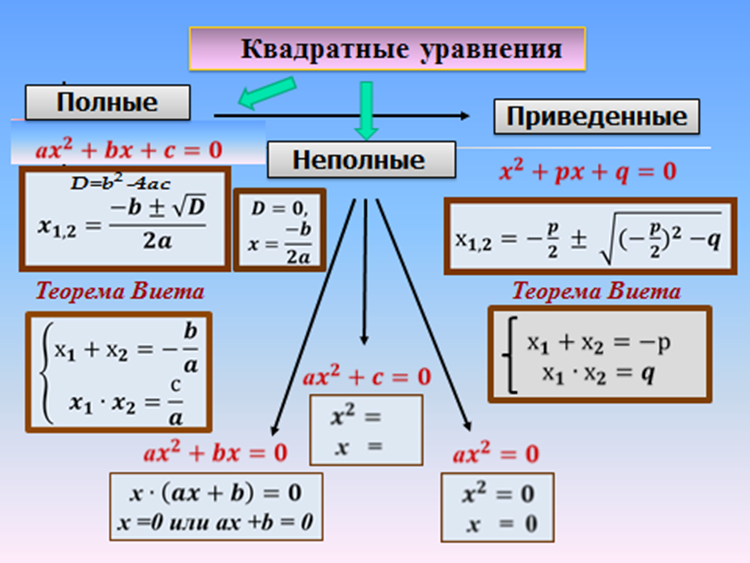
-Поставьте в оценочном листе по 1 баллу за правильный ответ.
Математический кросс
-А теперь предлагаю вам принять участие в математическом кроссе. Вам необходимо решить следующие уравнения, первые три ученика (победители кросса – помощники), выполнившие правильно задание заработают 2 балла, остальные, после проверки результатов помощниками, по 1 баллу:
 5х2-125=0 х1=5, х2= - 5
5х2-125=0 х1=5, х2= - 5
х2-5х=0 х1=0, х2= - 5
х2=36 х1=6, х2= - 6
-6х2=0 х=0
х2-5х+6=0 х1=2, х2= 3
Проверка результатов путем комментирования решения и ответа
-Поставьте в оценочном листе соответственно по 1-2 баллу за правильные решения.
Мини-кроссенс2
-А теперь мини-кроссенс поможет определить тему нашего урока. Посмотрите на набор картинок, найдите между ними связь и попробуйте сформулировать тему и цели урока


Они являются математическими моделями реальных ситуаций, поэтому решение различных практических задач сводится к их решению
-Поставьте в оценочном листе по 1 баллу за правильный ответ.
- Запишем тему урока: Дробно-рациональные уравнения
Цели урока:
1. Познакомиться с определением дробно- рационального уравнения, научиться их отличать от целых рациональных уравнений
2. Научиться решать простейшие дробно- рациональные уравнения (составить алгоритм решения).
3. Совершенствовать навыки решения квадратных уравнений
Актуализация и фиксирование индивидуальных затруднений в пробном учебном действии
-Какие выражения записаны на доске? (рациональные)
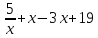
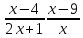
-Что объединяет следующие уравнения? (в левой и правой части рациональные выражения)
2х+5=3(8-х)
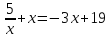
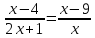
- Какое из следующих рациональных уравнений можем назвать дробным, а какое - целым?
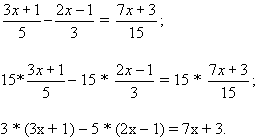

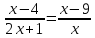
- Почему сложно определить? (Не знаем их определения)
-Откройте учебники на странице 139 и прочитайте:
-Какие уравнения называются рациональными?
-целыми рациональными?
-дробно-рациональными?
-Так какое из этих уравнений называется целым? А какое - дробным?
Выявление места и причины затруднения
-Рассмотрите пример 1 на стр. 139. Почему данное уравнение является целым? Сколько корней имеет это уравнение? Такие уравнения мы с вами уже решали.
- Рассмотрите Пример2 на стр. 140. Какой вид уравнения предлагается? А можем ли мы решать такие уравнения? Что нам необходимо сделать? (составить алгоритм решения)
Построение проекта выхода из затруднения и его реализация
-Ребята, перед вами составляющие алгоритма решения дробно-рационального уравнения. Работая в группе, определите правильную последовательность этих составляющих и приготовьтесь прокомментировать. На выполнение этого задания 2 минуты. Группа, которая справится раньше и сможет прокомментировать, заработают по 2 балла.
Алгоритм решения дробно - рационального уравнения
1. Найти наименьший общий знаменатель
2. Определить область допустимых значений данного уравнения
3. Определить дополнительные множители к каждой дроби и умножить на них числители уравнения, составив новое уравнение из выражений, полученных в числителях дробей
4. Упростить данное уравнение и решить его
5. Исключить корни, не входящие в область допустимых значений дробей уравнения
6. Записать ответ
(вариант для разрезания)
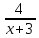 +
+ 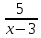 =
= 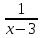 - 1
- 1
Найти наименьший общий знаменатель
(х-3)(х+3)
Определить область допустимых значений данного уравнения
ОДЗ: (х-3)(х+3) ≠0
х ≠-3, х≠3
Определить дополнительные множители к каждой дроби и умножить на них числители уравнения, составив новое уравнение из выражений, полученных в числителях дробей
4(х-3)+5(х+3)=(х+3)-(х+3)(х-3)
Упростить данное уравнение и решить его
 х2+8х-9=0
х2+8х-9=0
По теореме Виета: х1+х2=-8
х1*х2=-9 имеем х1=-9 х2=1
Исключить корни, не входящие в область допустимых значений дробей уравнения
Корни уравнения удовлетворяют ОДЗ
Записать ответ
Ответ: х1=-9 х2=1
-Поставьте в оценочном листе по 2 балла за правильный ответ.
Первичное закрепление с проговариванием во внешней речи
-Следующие уравнения будем решать вместе. Учащиеся, выполнившие задание у доски заработают по 2 балла за решение каждого уравнения



-Поставьте в оценочном листе по 2балла за правильный ответ.
7. Физминутка – зрительная гимнастика
-А теперь немного отдохнем, выполнив упражнения для глаз:
Сядьте ровно, расслабьтесь и, только водя зрачками, напишите ряд чисел от 0 до 9. Закройте глаза, откройте и быстро поморгайте. Хорошо, мы можем работать дальше.
Самостоятельная работа с самопроверкой по эталону
-Следующие уравнения решите по вариантам

- А теперь проверьте, правильно ли вы решили и поставьте себе за правильное решение – 2 балла.
1 вариант:
ОДЗ: х2+1≠0, х – все числа
х2+1 является дополнительным множителем к числу 2, получаем:
х2+3-2х2-2=0
-х2+1=0 – неполное квадратное уравнение, в=0
-х2=-1
х2=1
х1=1, х2= -1
Ответ: х1=1, х2= -1
2 вариант:
ОДЗ: х(х+2)≠0, х≠0, х≠-2
К первой дроби дополнительный множитель - х, ко второй – (х+2), получаем:
2х2-2х-4=0, разделим обе части уравнения на 2
 х2-х-2=0 – полное приведенное квадратное уравнение, решим по теореме Виета:
х2-х-2=0 – полное приведенное квадратное уравнение, решим по теореме Виета:
х1+ х2=1
х1*х2=-2, х1=2, х2= -1
Ответ: х1=2, х2= -1
-Поставьте в оценочном листе по 2 балла за правильный ответ.
Включение в систему знаний и повторения
-Кто правильно справился с самостоятельной работой, можете решать №602 (д,е,ж) и заработаете 2 балла
-Кому сложно, давайте проработаем следующие упражнения вместе № 601 (2 столбик), правильно выполняя которое, также можно заработать 2 балла
-Индивидуальное задание получают:
Боделан и Бенько № 605 (а,в) 3 балла
Панков и Шпара 604 (а) 3 балла
Рындин, Левчук, Руганова, Купринюк (карточка на повторение: назвать вид квадратного уравнения, выписать коэффициенты):
5х2-125=0 за выполнение задания получат 1 балл
х2-5х=0
х2=36
-6х2=0
х2-5х+6=0
Проверка работ
-Поставьте в оценочном листе по 1-3 балла соответственно за правильные ответы.
Рефлексия учебной деятельности
-А теперь давайте подсчитаем баллы, заработанные на уроке, если их количество 11 -13, то оценка «5», если – 8 -10 баллов, то – «4», если 5 - 7 баллов, то – «3».
- на уроке мне все было понятно,
я получил хорошие знания.
- усвоил материал, но осталось
выяснить некоторые вопросы.
- усвоил материал частично,
многого не понял.
Домашнее задание
-Проработать п. 25 стр. 139 , выполнить № 601 (в,г), 602 (в,г) , если материал усвоен на «4и 5», если ваш уровень достижений на «3», то № 601 (а,б)







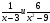
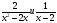
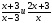
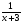
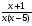
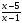




 5х2-125=0 х1=5, х2= - 5
5х2-125=0 х1=5, х2= - 5


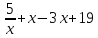
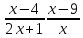
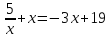
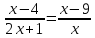
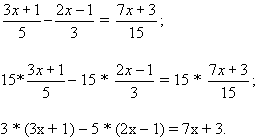

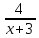 +
+ 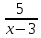 =
= 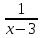 - 1
- 1 х2+8х-9=0
х2+8х-9=0




















