Решение геометрических задач ОГЭ №23 по теме "Окружность"

Решение задач ОГЭ

Геометрия № 23

Окружность

Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ = 24, а расстояние от центра окружности до хорд АВ и CD равны соответственно 16 и 12.

D

Дано: окр (О,r), АВ, СD- хорды, АВ=24,

OH ꓕ СD, ОТ ꓕ АВ, ОН=12, ОТ=16

Найти: CD

Н

С

О

Решение.

1) Рассмотрим треугольник АОВ- равнобедренный, так как ОА=ОВ=r, тогда высота ОТ является и медианой, т.е. АТ=ТВ=24:2=12.

А

Т

В

2)Треугольник АОТ- прямоугольный, по т.Пифагора

АО=20=ОВ=r=ОС=ОD

3) Аналогично, треугольник СОD-равнобедренный, СО=ОD, тогда ОH-высота,

является и медианой, т.е. СН=НD.

4) Рассмотрим треугольник прямоугольный СОН, по т.Пифагора найдем СН

СН=16=НD

5) Таким образом СD=16·2=32

Ответ: СD=32

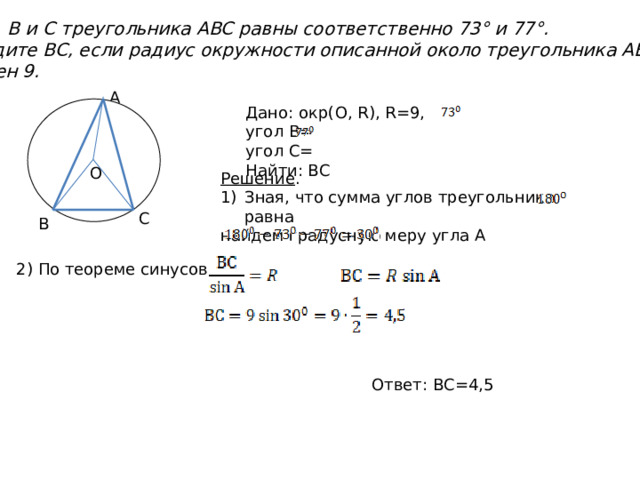
Углы B и C треугольника ABC равны соответственно 73° и 77°.

Найдите BC, если радиус окружности описанной около треугольника ABC,

равен 9.

А

Дано: окр(О, R), R=9, угол В=

угол С=

Найти: ВС

О

Решение .

• Зная, что сумма углов треугольника равна

найдем градусную меру угла А

С

В

2) По теореме синусов

Ответ: ВС=4,5

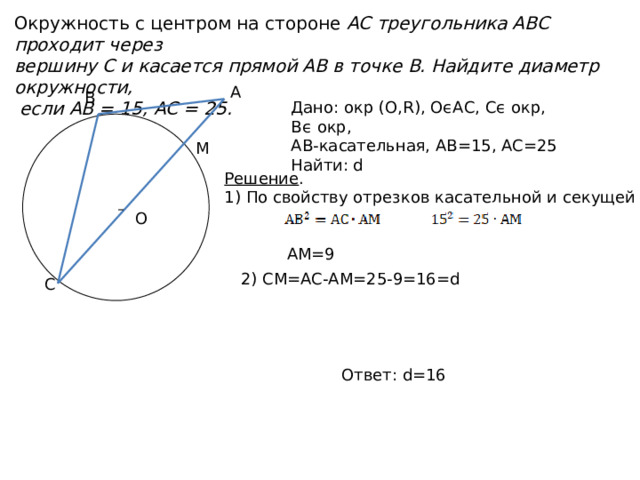
Окружность с центром на стороне AC треугольника ABC проходит через

вершину C и касается прямой AB в точке B. Найдите диаметр окружности,

если AB = 15, AC = 25.

А

В

Дано: окр (О,R), ОϵАС, Сϵ окр, Вϵ окр,

АВ-касательная, АВ=15, АС=25

Найти: d

М

Решение .

1) По свойству отрезков касательной и секущей

О

АМ=9

2) СМ=АС-АМ=25-9=16=d

С

Ответ: d=16

Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 2:3:7. Найдите радиус окружности,

если меньшая из сторон равна 16.

С

Дано: ∆ АВС, окр (О, R), А,В,С ϵ окр,

В

АВ=16

Найти: R

О

А

Решение .

• Градусная мера окружности равна

Тогда вычислим градусные меры дуг

2) Угол АСВ опирается на дугу АВ, вписанный, поэтому градусная мера угла АСВ=

половине градусной меры дуги АВ=

3) По теореме синусов

R=16

Ответ: R=16

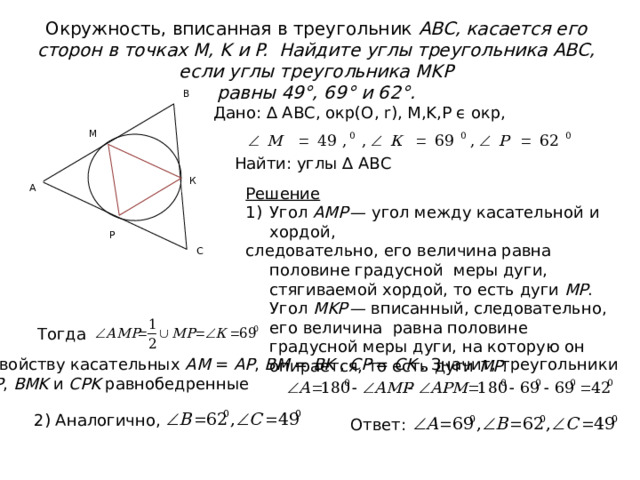
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP

равны 49°, 69° и 62°.

В

Дано: ∆ АВС, окр(О, r), М,K,P ϵ окр,

M

Найти: углы ∆ АВС

К

А

Решение

• Угол  AMP  — угол между касательной и хордой,

следовательно, его величина равна половине градусной меры дуги, стягиваемой хордой, то есть дуги  MP . Угол  MKP  — вписанный, следовательно, его величина равна половине градусной меры дуги, на которую он опирается, то есть дуги  MP .

P

С

Тогда

По свойству касательных  AM  =  AP ,  BM  =  BK  ,  CP  =  CK  . Значит, треугольники

  AMP ,  BMK  и  CPK  равнобедренные

2) Аналогично,

Ответ:

Окружность пересекает стороны AB и AC треугольника ABC в точках K и P

соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC.

Дано: окр(О, R), ∆ АВС, В,С ϵ окр,

АВ ∩ окр=К, АС ∩ окр =Р, АК=18,

АС ˃ ВС в 1,2 раза

Найти: КР

А

К

В

Р

Решение .

• Рассмотрим четырехугольник ВСРК- вписанный в окружность,

значит сумма противоположных углов равна 180 0 , т.е.

С

2) Рассмотрим треугольники АВС и АРК: угол А – общий,

Следовательно, эти треугольники подобны по двум углам.

Запишем пропорциональность сторон

Ответ: КР=15

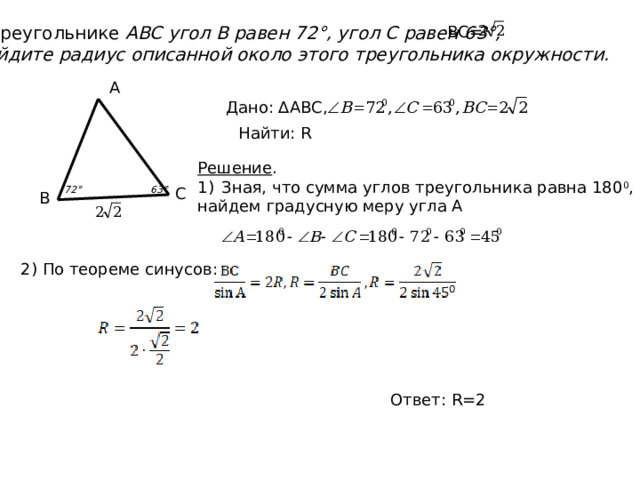
В треугольнике ABC угол B равен 72°, угол C равен 63°,

ВС=

Найдите радиус описанной около этого треугольника окружности.

А

Дано: ∆АВС,

Найти: R

Решение .

• Зная, что сумма углов треугольника равна 180 0 ,

найдем градусную меру угла А

63°

72°

С

В

2) По теореме синусов:

Ответ: R=2

В треугольнике ABC угол C равен 90°, вписанной окружности равен 2.

площадь треугольника ABC, если 12. АB=12

Дано: ∆АВС,

окр(О,r), r=2, АВ=12

В

Найти:

F

Решение .

1) По свойству отрезков касательных, проведенных

из одной точки: МС=СК=r=2, а также АМ=АF,BF=BK

К

О

С

2)

А

М

3)

Ответ:

Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если 14. BH =14