ЗАДАНИЕ 26 ОГЭ.
ГЕОМЕТРИЧЕСКАЯ ЗАДАЧА ПОВЫШЕННОЙ СЛОЖНОСТИ.
ОКРУЖНОСТИ
(316245) Три окружности с центрами 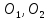 и
и 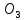 и радиусами
и радиусами  и
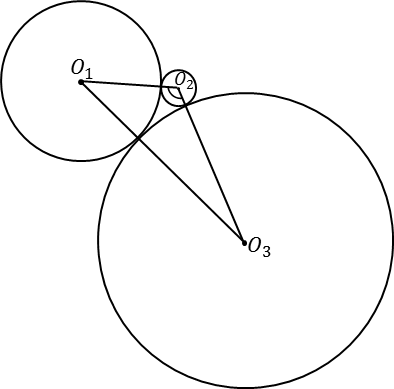
и 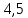 соответственно попарно касаются внешним образом. Найдите угол
соответственно попарно касаются внешним образом. Найдите угол 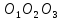 .
.
Решение.
1). Найдём стороны треугольника 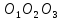 .
.
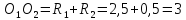

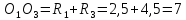
2). Воспользуемся теоремой косинусов для стороны  .
.


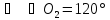
Ответ: 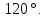
(316335) Две окружности с центрами  и
и 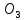 и радиусами
и радиусами 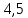 и
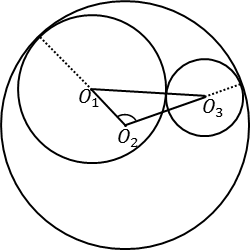
и 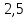 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром
касаются друг с другом внешним образом и внутренним образом касаются окружности с центром 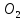 и радиусом
и радиусом  . Найдите угол
. Найдите угол 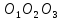 .
.
Решение.
1). Найдём стороны треугольника 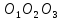 .
.


2). Воспользуемся теоремой косинусов для стороны  .
.


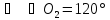
Ответ: 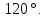
(311568) Три окружности, радиусы которых равны  и
и  , попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.
, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.
Решение.
1). Найдём стороны треугольника 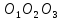 .
.



2). Окружность, вписанная в треугольник 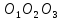 имеет радиус
имеет радиус  . Найдём этот радиус из формулы площади треугольника.
. Найдём этот радиус из формулы площади треугольника.

Ответ: 
(333027) Две касающиеся внешним образом в точке  окружности, радиусы которых равны
окружности, радиусы которых равны  и
и  , вписаны в угол с вершиной
, вписаны в угол с вершиной  . Общая касательная к этим окружностям, проходящая через точку
. Общая касательная к этим окружностям, проходящая через точку  , пересекает стороны угла в точках
, пересекает стороны угла в точках  и
и  . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника  .
.
Решение. Дан угол  ; две касающиеся внешним образом окружности с центрами в точках
; две касающиеся внешним образом окружности с центрами в точках  и
и 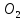 , и радиусами
, и радиусами  и
и  соответственно; общая касательная
соответственно; общая касательная  , проходящая через точку
, проходящая через точку  .
.
1). По теореме: «Если окружность вписана в угол, то её центр лежит на биссектрисе этого угла» получаем, что биссектриса угла  проходит через центры
проходит через центры  и
и 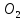 данных окружностей. К тому же она проходит через точку
данных окружностей. К тому же она проходит через точку  , т.к. эта точка является точкой касания двух окружностей, значит, лежит на прямой
, т.к. эта точка является точкой касания двух окружностей, значит, лежит на прямой  (более развёрнуто: радиусы
(более развёрнуто: радиусы  и
и  перпендикулярны касательной
перпендикулярны касательной  , значит, , т.е.
, значит, , т.е.  – развёрнутый).
– развёрнутый).
2). Так как  является биссектрисой и высотой, то
является биссектрисой и высотой, то  – равнобедренный, и
– равнобедренный, и  является медианой, т.е.
является медианой, т.е.  и
и  .
.
3). Проведём радиусы  и
и  в точки касания данных окружностей и касательной
в точки касания данных окружностей и касательной  . Рассмотрим
. Рассмотрим  и
и  .
.
по I признаку подобия треугольников. Следовательно, соответствующие стороны у них пропорциональны, т.е. .
Пусть  , тогда . Рассмотрим первые два отношения первой пропорции.
, тогда . Рассмотрим первые два отношения первой пропорции.
Значит,  , тогда , и из
, тогда , и из  по теореме Пифагора, .
по теореме Пифагора, .
Рассмотрим первое и третье отношение во второй пропорции.
.
4). В треугольнике 
 , т.е. катет равен половине гипотенузы, значит, по свойству угла, равного
, т.е. катет равен половине гипотенузы, значит, по свойству угла, равного  ,
,  . Следовательно,
. Следовательно,  . Так как
. Так как  – равнобедренный, то, по сумме углов треугольника,
– равнобедренный, то, по сумме углов треугольника,
. Все три угла в треугольнике равны, значит,  – равносторонний, т.е.
– равносторонний, т.е.  .
.
5). В равностороннем треугольнике центры вписанной и описанной окружности совпадают, значит, радиусом окружности, описанной около  является отрезок
является отрезок  .
.
Ответ: 
(311562) Окружность радиуса  касается внешним образом второй окружности в точке
касается внешним образом второй окружности в точке  . Общая касательная к этим окружностям, проходящая через точку
. Общая касательная к этим окружностям, проходящая через точку  , пересекается с некоторой другой их общей касательной в точке
, пересекается с некоторой другой их общей касательной в точке  . Найдите радиус второй окружности, если
. Найдите радиус второй окружности, если  .
.
Решение. Даны две касающиеся внешним образом окружности с центрами с точках  и
и 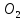 , и радиусами
, и радиусами  и
и  ; общая касательная
; общая касательная  , проходящая через точку касания окружностей
, проходящая через точку касания окружностей  и общая касательная
и общая касательная  , пересекающая касательную
, пересекающая касательную  в точке
в точке  ;
;  .
.
1). Проведём радиусы  и
и  . Отрезок, соединяющий радиусы касающихся окружностей проходит через точку касания, т.е.
. Отрезок, соединяющий радиусы касающихся окружностей проходит через точку касания, т.е.  . Значит,
. Значит,  . Касательная перпендикулярна радиусу, проведённому в точку касания, поэтому,
. Касательная перпендикулярна радиусу, проведённому в точку касания, поэтому,  и
и  . Следовательно,
. Следовательно,  .
.
2). Поскольку отрезки касательных, проведённых из одной точки (точки  ), равны, то
), равны, то  и
и  , значит,
, значит,  , тогда
, тогда  .
.
3). Проведём  , тогда
, тогда  и четырёхугольник
и четырёхугольник  является прямоугольником, и
является прямоугольником, и  , и
, и  . Значит,
. Значит,  .
.
4). Рассмотрим треугольник  . Он прямоугольный, значит, мы вправе использовать теорему Пифагора.
. Он прямоугольный, значит, мы вправе использовать теорему Пифагора.





Значит, радиус второй окружности  .
.
Ответ: 
(311670) В окружности с центром в точке  проведены две хорды
проведены две хорды  и
и  . Прямые
. Прямые  и
и  перпендикулярны и пересекаются в точке
перпендикулярны и пересекаются в точке  , лежащей вне окружности. При этом, . Найдите
, лежащей вне окружности. При этом, . Найдите  .
.
Решение.
1). Проведём радиусы  . Опустим перпендикуляры
. Опустим перпендикуляры  и
и  на хорды
на хорды  и
и  . Тогда четырёхугольник
. Тогда четырёхугольник  является прямоугольником, значит,
является прямоугольником, значит,  и
и  .
.
2). По свойству высоты равнобедренного треугольника,  и
и  являются медианами, т.е.
являются медианами, т.е.
 .
.
3). . Из треугольника  , по теореме Пифагора, находим радиус
, по теореме Пифагора, находим радиус  .
.
4). Из треугольника  , по теореме Пифагора, находим высоту
, по теореме Пифагора, находим высоту  .
.
5). Из треугольника  , по теореме Пифагора, находим искомый отрезок
, по теореме Пифагора, находим искомый отрезок 
Ответ: 
(311708) В прямоугольном треугольнике  с прямым углом
с прямым углом  , проведена биссектриса угла
, проведена биссектриса угла  . Известно, что она пересекает серединный перпендикуляр, проведённый к стороне
. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне  , в точке
, в точке  . Найдите угол
. Найдите угол  , если известно, что угол
, если известно, что угол  равен
равен  .
.
Решение.
1). Дан (по сумме углов треугольника).
2).  – биссектриса
– биссектриса  .
.
3).  – серединный перпендикуляр к стороне
– серединный перпендикуляр к стороне  , следовательно, он параллелен стороне
, следовательно, он параллелен стороне  , и, значит, делит гипотенузу пополам (по теореме Фалеса: «Если параллельные прямые отсекают на одной стороне угла равные отрезки, то на другой стороне угла они отсекают также равные отрезки»).
, и, значит, делит гипотенузу пополам (по теореме Фалеса: «Если параллельные прямые отсекают на одной стороне угла равные отрезки, то на другой стороне угла они отсекают также равные отрезки»).
4).  – секущая, тогда (как внутренние накрест лежащие при параллельных прямых). Тогда
– секущая, тогда (как внутренние накрест лежащие при параллельных прямых). Тогда  – равнобедренный, т.е.
– равнобедренный, т.е.  .
.
5). Точка  – середина гипотенузы является центром окружности, описанной около треугольника
– середина гипотенузы является центром окружности, описанной около треугольника  , значит,
, значит,  и
и  являются радиусами этой окружности, т.е. окружность проходит через вершины треугольника и точку
являются радиусами этой окружности, т.е. окружность проходит через вершины треугольника и точку  .
.
6). По свойству вписанных углов, опирающихся на одну дугу (или хорду), вписанные углы  и
и  равны, т.е.
равны, т.е.  .
.
Ответ: 
(333132) Окружности радиусов  и
и  касаются внешним образом. Точки
касаются внешним образом. Точки  и
и  лежат на первой окружности, точки
лежат на первой окружности, точки  и
и  – на второй. При этом,
– на второй. При этом,  и
и  – общие касательные окружностей. Найдите расстояние между прямыми
– общие касательные окружностей. Найдите расстояние между прямыми  и
и  .
.
Решение. Даны две касающиеся внешним образом окружности с центрами в точках  и
и 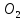 , и радиусами
, и радиусами  ; две общие касательные этих окружностей
; две общие касательные этих окружностей  и
и  , которые мы продлим до пересечения в точке
, которые мы продлим до пересечения в точке  .
.
1). По свойству касательных, выходящих из одной точки,  и
и  . Поэтому,
. Поэтому,  .
.
2). Рассмотрим  и
и  .
.
по II признаку подобия треугольников, значит,  и т.к. они соответственные, то
и т.к. они соответственные, то  (по свойству параллельных прямых).
(по свойству параллельных прямых).
3). Расстоянием между двумя параллельными прямыми является длина общего перпендикуляра к этим прямым. В нашем случае это отрезок  . Почему? Объясняем.
. Почему? Объясняем.
Поскольку  и
и  равнобедренные, то биссектриса
равнобедренные, то биссектриса  угла
угла  является высотой и медианой, т.е.
является высотой и медианой, т.е.  и
и  . Значит, отрезок
. Значит, отрезок  , который является частью биссектрисы
, который является частью биссектрисы  также перпендикулярен
также перпендикулярен  и
и  . Итак, наша задача найти
. Итак, наша задача найти  .
.
4). Проведём перпендикуляр  из точки
из точки  на радиус второй окружности
на радиус второй окружности  . Четырёхугольник
. Четырёхугольник  является прямоугольником, т.к. радиусы
является прямоугольником, т.к. радиусы  и
и  перпендикулярны касательной, проведённой в точку касания. Значит,
перпендикулярны касательной, проведённой в точку касания. Значит,  . Тогда .
. Тогда .
5). Из треугольника  , находим косинус угла
, находим косинус угла 
6).  как соответственные при параллельных прямых, поэтому, из треугольника
как соответственные при параллельных прямых, поэтому, из треугольника 
.
Из треугольника  .
.
7). Теперь найдём  .
.
Ответ: 
(353564) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
Решение.
1). В четырёхугольнике  точка
точка  – середина стороны
– середина стороны  , значит,
, значит,  . По условию задачи, точка
. По условию задачи, точка  равноудалена от всех вершин четырёхугольника, значит,
равноудалена от всех вершин четырёхугольника, значит,  . А это означает, что точка
. А это означает, что точка  является радиусом окружности, описанной около четырёхугольника
является радиусом окружности, описанной около четырёхугольника  . По свойству описанной окружности, . Тогда .
. По свойству описанной окружности, . Тогда .
2).  – равнобедренный, значит,
– равнобедренный, значит,  . Тогда
. Тогда 
 .
.  – тоже равнобедренный, значит,
– тоже равнобедренный, значит,  .
.
3). По сумме углов треугольника .
4). Из , по теореме Пифагора, . Тогда  .
.
Ответ:  .
.
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(311862, 316272) Три окружности с центрами 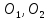 и
и 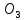 и радиусами
и радиусами  и
и  соответственно попарно касаются внешним образом. Найдите угол
соответственно попарно касаются внешним образом. Найдите угол 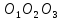 .
.
(316298) Три окружности с центрами 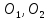 и
и 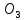 и радиусами
и радиусами  и
и  соответственно попарно касаются внешним образом. Найдите угол
соответственно попарно касаются внешним образом. Найдите угол 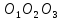 .
.
(311774) Две окружности с центрами  и
и 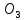 и радиусами
и радиусами  и
и  касаются друг с другом внешним образом и внутренним образом касаются окружности с центром
касаются друг с другом внешним образом и внутренним образом касаются окружности с центром 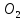 и радиусом
и радиусом  . Найдите угол
. Найдите угол 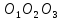 .
.
(333106) Две касающиеся внешним образом в точке  окружности, радиусы которых равны
окружности, радиусы которых равны  и
и  , вписаны в угол с вершиной
, вписаны в угол с вершиной  . Общая касательная к этим окружностям, проходящая через точку
. Общая касательная к этим окружностям, проходящая через точку  , пересекает стороны угла в точках
, пересекает стороны угла в точках  и
и  . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника  .
.
(340378) Две касающиеся внешним образом в точке  окружности, радиусы которых равны
окружности, радиусы которых равны  и
и  , вписаны в угол с вершиной
, вписаны в угол с вершиной  . Общая касательная к этим окружностям, проходящая через точку
. Общая касательная к этим окружностям, проходящая через точку  , пересекает стороны угла в точках
, пересекает стороны угла в точках  и
и  . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника  .
.
(353476) Две касающиеся внешним образом в точке  окружности, радиусы которых равны
окружности, радиусы которых равны  и
и  , вписаны в угол с вершиной
, вписаны в угол с вершиной  . Общая касательная к этим окружностям, проходящая через точку
. Общая касательная к этим окружностям, проходящая через точку  , пересекает стороны угла в точках
, пересекает стороны угла в точках  и
и  . Найдите радиус окружности, описанной около треугольника
. Найдите радиус окружности, описанной около треугольника  .
.
(333159) Окружности радиусов  и
и  касаются внешним образом. Точки
касаются внешним образом. Точки  и
и  лежат на первой окружности, точки
лежат на первой окружности, точки  и
и  – на второй. При этом,
– на второй. При этом,  и
и  – общие касательные окружностей. Найдите расстояние между прямыми
– общие касательные окружностей. Найдите расстояние между прямыми  и
и  .
.
(352993) Окружности радиусов  и
и  касаются внешним образом. Точки
касаются внешним образом. Точки  и
и  лежат на первой окружности, точки
лежат на первой окружности, точки  и
и  – на второй. При этом,
– на второй. При этом,  и
и  – общие касательные окружностей. Найдите расстояние между прямыми
– общие касательные окружностей. Найдите расстояние между прямыми  и
и  .
.
(350474) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(350898) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(350970) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(351323) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(351705) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(352889) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(353463) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
(353491) Середина  стороны
стороны  выпуклого четырёхугольника равноудалена от всех его вершин. Найдите
выпуклого четырёхугольника равноудалена от всех его вершин. Найдите  , если
, если  , а углы
, а углы  и
и  четырёхугольника равны соответственно
четырёхугольника равны соответственно  и
и  .
.
ОТВЕТЫ
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
|
| № задания | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| ответ | 
| 
| 
| 
| 
| 
| 
| 
|
4







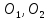 и
и 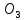 и радиусами
и радиусами  и
и 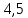 соответственно попарно касаются внешним образом. Найдите угол
соответственно попарно касаются внешним образом. Найдите угол 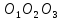 .
.
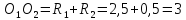

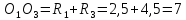
 .
.

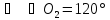
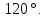
 и
и 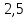 касаются друг с другом внешним образом и внутренним образом касаются окружности с центром
касаются друг с другом внешним образом и внутренним образом касаются окружности с центром 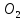 и радиусом
и радиусом  . Найдите угол
. Найдите угол 











