ЗАДАНИЕ 24 ОГЭ.
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ВЫЧИСЛЕНИЕ.
ОКРУЖНОСТИ.
(311650) В треугольнике  угол
угол 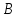 равен
равен 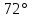 , а угол
, а угол 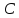 равен
равен 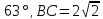 . Найдите радиус описанной около этого треугольника окружности.
. Найдите радиус описанной около этого треугольника окружности.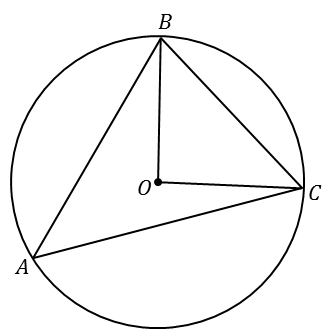
Решение.
I способ. Проведём радиусы 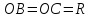 . По сумме углов треугольника:
. По сумме углов треугольника:
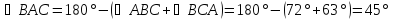 . Этот угол является вписанным, а ему соответствующий центральный угол -
. Этот угол является вписанным, а ему соответствующий центральный угол - 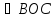 . По свойству вписанного угла: «Вписанный угол равен половине центрального угла, опирающегося на ту же дугу»,
. По свойству вписанного угла: «Вписанный угол равен половине центрального угла, опирающегося на ту же дугу», 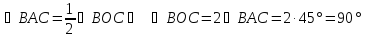 . Значит,
. Значит, 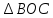 – прямоугольный. По теореме Пифагора:
– прямоугольный. По теореме Пифагора:
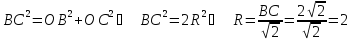 .
.
II способ. 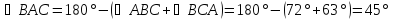 (т.к. сумма углов треугольника равна
(т.к. сумма углов треугольника равна 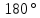 ). Воспользуемся теоремой синусов: «Стороны треугольника пропорциональны синусам противолежащих углов, причём, коэффициент пропорциональности равен диаметру описанной окружности», т.е.
). Воспользуемся теоремой синусов: «Стороны треугольника пропорциональны синусам противолежащих углов, причём, коэффициент пропорциональности равен диаметру описанной окружности», т.е.
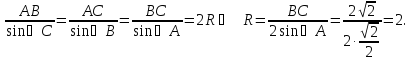
Ответ: 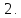
(340853) Окружность с центром на стороне  треугольника
треугольника  проходит через вершину
проходит через вершину 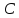 и касается прямой
и касается прямой  в точке
в точке 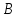 . Найдите диаметр окружности, если
. Найдите диаметр окружности, если 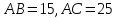 .
.
Решение.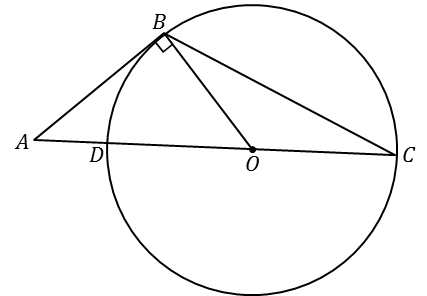
I способ.  – касательная к окружности,
– касательная к окружности,  – секущая,
– секущая,  . Воспользуемся свойством: «Произведение секущей на её внешнюю часть равна квадрату отрезка касательной», т.е.
. Воспользуемся свойством: «Произведение секущей на её внешнюю часть равна квадрату отрезка касательной», т.е. 
. Тогда диаметр .
II способ. Не все помнят свойство касательной и секущей, поэтому приведём другой способ решения. Т.к.  – касательная, то она перпендикулярна радиусу, проведённому в точку касания, т.е.
– касательная, то она перпендикулярна радиусу, проведённому в точку касания, т.е.  . Из прямоугольного треугольника
. Из прямоугольного треугольника  , где
, где  , по теореме Пифагора,
, по теореме Пифагора,  . Так как
. Так как  , то
, то
.
Значит, диаметр .
Ответ:  .
.
(340879) Окружность, вписанная в треугольник  , касается его сторон в точках
, касается его сторон в точках  и
и  . Найдите углы треугольника
. Найдите углы треугольника  , если углы треугольника
, если углы треугольника  равны
равны  и
и  .
.
Решение. Пусть .
I способ.
Введём обозначения: .
Воспользуемся свойством касательных: «Отрезки касательных, проведённых из общей точки, равны», т.е. . Значит, – равнобедренные, следовательно,
. Найдём выражение этих углов через введённые обозначения, используя свойство углов треугольника.
Составим формулы для нахождения углов треугольника  .
.
Составим систему уравнений, учитывая, что .
Значит, .
II способ. Угол между касательными иногда называют описанным углом. Известно свойство, что описанный угол равен полуразности дуг, на которые он опирается, т.е. . Также известно, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается. Поэтому
. Значит,
.
Выполняя аналогичные рассуждения, определяем другие два угла треугольника  .
.
, .
Так как углы треугольника  – вписанные в окружность, то они равны половине соответствующих центральных углов, т.е.
– вписанные в окружность, то они равны половине соответствующих центральных углов, т.е.
Теперь можем найти искомые углы.
Ответ: 
(339492) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 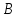 и
и 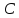 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
Решение.
I способ. Стороны  и
и  являются секущими для окружности, поэтому,
являются секущими для окружности, поэтому,  («Произведения длин отрезков секущих, проведённых из общей точки, равны»). Значит,
(«Произведения длин отрезков секущих, проведённых из общей точки, равны»). Значит,  .
.
Рассмотрим  и
и  .
.
по II признаку подобия треугольников. Значит,
II способ. Т.к. четырёхугольник  – вписанный, то сумма его противоположных углов равна
– вписанный, то сумма его противоположных углов равна 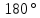 , т.е. . По свойству смежных углов
, т.е. . По свойству смежных углов
. Тогда, .
Рассмотрим  и
и  .
.
по I признаку подобия треугольников. Значит,
Ответ:
(359979) Отрезки  и
и  являются хордами окружности. Найдите длину хорды
являются хордами окружности. Найдите длину хорды  , если
, если  , а расстояние от центра окружности до хорд
, а расстояние от центра окружности до хорд  и
и  равны соответственно
равны соответственно  и
и  .
.
Решение.
Опустим перпендикуляры  и
и  на хорды
на хорды  и
и  соответственно. Так как – радиусы, то треугольники
соответственно. Так как – радиусы, то треугольники  и
и  – равнобедренные. По свойству равнобедренного треугольника («В равнобедренном треугольнике высота, проведённая к основанию является биссектрисой и медианой»), .
– равнобедренные. По свойству равнобедренного треугольника («В равнобедренном треугольнике высота, проведённая к основанию является биссектрисой и медианой»), .
Рассмотрим  и
и 
по признаку равенства прямоугольных треугольников (по катету и гипотенузе). Значит, .
Ответ:  .
.
ЗАДАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(311651) В треугольнике  угол
угол 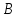 равен
равен  , а угол
, а угол 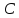 равен
равен  . Найдите радиус описанной около этого треугольника окружности.
. Найдите радиус описанной около этого треугольника окружности.
(339535) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 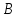 и
и 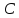 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(339676) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 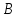 и
и 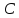 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(339857) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 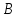 и
и 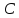 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(339913) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 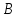 и
и 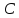 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(339957) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 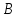 и
и 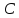 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(350422) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 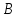 и
и 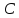 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(350713) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 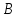 и
и 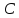 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(350889) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 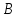 и
и 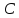 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза меньше стороны
раза меньше стороны  .
.
(351596) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 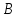 и
и 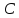 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза меньше стороны
раза меньше стороны  .
.
(351668) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 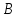 и
и 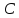 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(351686) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 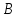 и
и 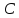 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза меньше стороны
раза меньше стороны  .
.
(351714) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 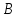 и
и 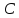 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза больше стороны
раза больше стороны  .
.
(353588) Окружность пересекает стороны  и
и  треугольника
треугольника  в точках
в точках  и
и  соответственно и проходит через вершины
соответственно и проходит через вершины 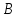 и
и 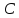 . Найдите длину отрезка
. Найдите длину отрезка  , если
, если  , а сторона
, а сторона  в
в  раза меньше стороны
раза меньше стороны  .
.
(360042) Отрезки  и
и  являются хордами окружности. Найдите длину хорды
являются хордами окружности. Найдите длину хорды  , если
, если  , а расстояние от центра окружности до хорд
, а расстояние от центра окружности до хорд  и
и  равны соответственно
равны соответственно  и
и  .
.
ОТВЕТЫ
| № задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| ответ | 3 | 17 | 7 | 14 | 3 | 4 | 20 | 25 | 25 | 14 | 10 | 7 | 5 | 3 | 30 |
3







 угол
угол 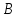 равен
равен 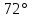 , а угол
, а угол 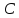 равен
равен 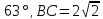 . Найдите радиус описанной около этого треугольника окружности.
. Найдите радиус описанной около этого треугольника окружности.
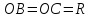 . По сумме углов треугольника:
. По сумме углов треугольника: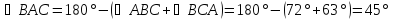 . Этот угол является вписанным, а ему соответствующий центральный угол -
. Этот угол является вписанным, а ему соответствующий центральный угол - 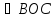 . По свойству вписанного угла: «Вписанный угол равен половине центрального угла, опирающегося на ту же дугу»,
. По свойству вписанного угла: «Вписанный угол равен половине центрального угла, опирающегося на ту же дугу», 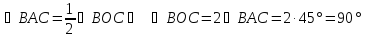 . Значит,
. Значит, 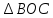 – прямоугольный. По теореме Пифагора:
– прямоугольный. По теореме Пифагора: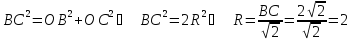 .
. ). Воспользуемся теоремой синусов: «Стороны треугольника пропорциональны синусам противолежащих углов, причём, коэффициент пропорциональности равен диаметру описанной окружности», т.е.
). Воспользуемся теоремой синусов: «Стороны треугольника пропорциональны синусам противолежащих углов, причём, коэффициент пропорциональности равен диаметру описанной окружности», т.е.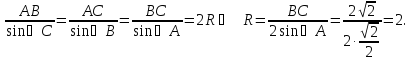
 треугольника
треугольника  в точке
в точке 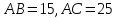 .
.