Теоретическая часть разработки содержит всевозможные задачи, которые используются на экзамене в 9 классе. Приведены все задачи, относящиеся к заданию № 25 "Окружности и их элементы". К аналогичным заданиям приведены решения, некоторые содержат 2 способа решения. В практической части разработки приведены все остальные задачи, по своему содержанию схожие с решёнными. Разработка поможет тем, кто хочет получить хорошую оценку на ОГЭ, а также будет полезна и тем, кто готовится к ЕГЭ.
Просмотр содержимого документа
«Задание 25. Окружности и их элементы.»
ЗАДАНИЕ 25 ОГЭ.
ОКРУЖНОСТИ И ИХ ЭЛЕМЕНТЫ.
(311241) В окружности с центром 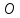 проведены две хорды
проведены две хорды 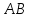 и
и  так, что центральные углы
так, что центральные углы 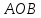 и
и  равны. На эти хорды опущены перпендикуляры
равны. На эти хорды опущены перпендикуляры  и
и  . Докажите, что
. Докажите, что  и
и  равны.
равны.
Решение. Рассмотрим 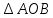 и
и  .
.
 (по I признаку равенства треугольников). Следовательно, все соответствующие элементы этих треугольников равны, а именно:
(по I признаку равенства треугольников). Следовательно, все соответствующие элементы этих треугольников равны, а именно:  , ч.т.д.
, ч.т.д.

(341422) Окружности с центрами в точках  и
и  пересекаются в точках
пересекаются в точках  и
и  , причём, точки
, причём, точки  и
и  лежат по одну сторону от прямой
лежат по одну сторону от прямой 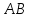 . Докажите, что отрезки
. Докажите, что отрезки 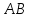 и
и 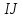 перпендикулярны.
перпендикулярны.
Решение.
Т.к. окружности пересекаются по прямой 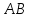 , то
, то  , т.е. точка
, т.е. точка  равноудалена от точек
равноудалена от точек  и
и  , и точка
, и точка  равноудалена от точек
равноудалена от точек  и
и  . Значит, они лежат на серединном перпендикуляре к отрезку
. Значит, они лежат на серединном перпендикуляре к отрезку 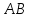 . Т.к. серединный перпендикуляр единственный, то точки
. Т.к. серединный перпендикуляр единственный, то точки  и
и  лежат на одной прямой, и эта прямая
лежат на одной прямой, и эта прямая  , значит,
, значит,  , ч.т.д.
, ч.т.д.
(311258) В окружности с центром 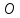 проведены две равные хорды
проведены две равные хорды  и
и  . На эти хорды опущены перпендикуляры
. На эти хорды опущены перпендикуляры  и
и  . Докажите, что
. Докажите, что  и
и  равны.
равны.
Решение. Рассмотрим  и
и  .
.
(по III признаку равенства треугольников). Следовательно, все соответствующие элементы этих треугольников равны, а, значит, и их высоты:  , ч.т.д.
, ч.т.д.
(316360) В окружности через середину 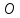 хорды
хорды  проведена хорда
проведена хорда  так, что дуги
так, что дуги 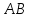 и
и  равны. Докажите, что
равны. Докажите, что 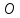 – середина хорды
– середина хорды  .
.
Решение.
I способ. Вспомним свойство хорды: «Если радиус (диаметр) проходит через середину хорды, то он перпендикулярен этой хорде»
По условию, точка 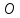 - середина хорды
- середина хорды  , значит,
, значит,  перпендикулярна радиусу, проведённому через точку
перпендикулярна радиусу, проведённому через точку 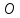 . Если
. Если 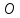 - середина хорды
- середина хорды  , то
, то  перпендикулярна тому же самому радиусу, проведённому в точку
перпендикулярна тому же самому радиусу, проведённому в точку 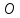 . Мы получаем, что через точку
. Мы получаем, что через точку 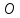 проведены две прямые, перпендикулярные одной и той же прямой, а это невозможно. Это означает, что середина хорды
проведены две прямые, перпендикулярные одной и той же прямой, а это невозможно. Это означает, что середина хорды  совпадает с центром окружности. Так как хорда
совпадает с центром окружности. Так как хорда  проходит через точку
проходит через точку 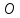 – центр окружности, то она является диаметром, значит,
– центр окружности, то она является диаметром, значит,  , т.е.
, т.е. 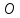 - середина
- середина  , ч.т.д.
, ч.т.д.
II способ. Проведём отрезки  и
и  . Вписанные углы
. Вписанные углы  и
и  опираются на одну и ту же дугу
опираются на одну и ту же дугу  , значит, они равны (по свойству вписанных углов). Аналогично, вписанные углы
, значит, они равны (по свойству вписанных углов). Аналогично, вписанные углы  и
и  опираются на одну и ту же дугу
опираются на одну и ту же дугу 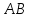 , значит, они тоже равны. По условию задачи, дуги
, значит, они тоже равны. По условию задачи, дуги 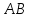 и
и  равны, поэтому все эти вписанные углы равны между собой, т.е.
равны, поэтому все эти вписанные углы равны между собой, т.е.  .
.
Значит,  и
и  равнобедренные, и
равнобедренные, и  . А т.к.
. А т.к.  , то и
, то и  , т.е. точка
, т.е. точка 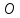 - середина хорды
- середина хорды  , ч.т.д.
, ч.т.д.
(340324) Окружности с центрами в точках  и
и  не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении
не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении  . Докажите, что диаметры этих окружностей относятся как
. Докажите, что диаметры этих окружностей относятся как  .
.
Решение.
Пусть  – общая касательная к данным окружностям. Она касается этих окружностей в точках
– общая касательная к данным окружностям. Она касается этих окружностей в точках  и
и  и пересекает отрезок
и пересекает отрезок  в точке
в точке  . По свойству касательной: «Касательная перпендикулярна радиусу окружности, проведённому в точку касания», получаем, что
. По свойству касательной: «Касательная перпендикулярна радиусу окружности, проведённому в точку касания», получаем, что  .
.
Рассмотрим  и
и  .
.
(по I признаку подобия треугольников) . Другими словами,  . Но , ч.т.д.
. Но , ч.т.д.
ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(357110) Окружности с центрами в точках  и 𝑁 пересекаются в точках
и 𝑁 пересекаются в точках  и
и  , причём, точки
, причём, точки  и
и  лежат по одну сторону от прямой
лежат по одну сторону от прямой  . Докажите, что отрезки
. Докажите, что отрезки  и
и  перпендикулярны.
перпендикулярны.
(352846) Окружности с центрами в точках  и Q пересекаются в точках
и Q пересекаются в точках  и
и  , причём, точки
, причём, точки  и
и  лежат по одну сторону от прямой
лежат по одну сторону от прямой  . Докажите, что прямые
. Докажите, что прямые  и
и  перпендикулярны.
перпендикулярны.
(316386) В окружности через середину 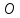 хорды
хорды  проведена хорда
проведена хорда  так, что дуги
так, что дуги 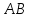 и
и  равны. Докажите, что
равны. Докажите, что 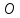 – середина хорды
– середина хорды  .
.
(349626) Окружности с центрами в точках  и
и  не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении
не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении  . Докажите, что диаметры этих окружностей относятся как
. Докажите, что диаметры этих окружностей относятся как  .
.
(357111) Окружности с центрами в точках  и
и  не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении
не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении  . Докажите, что диаметры этих окружностей относятся как
. Докажите, что диаметры этих окружностей относятся как  .
.
2







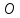 проведены две хорды
проведены две хорды 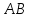 и
и  так, что центральные углы
так, что центральные углы 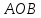 и
и  равны. На эти хорды опущены перпендикуляры
равны. На эти хорды опущены перпендикуляры  и
и  . Докажите, что
. Докажите, что 
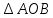 и
и  .
. (по I признаку равенства треугольников). Следовательно, все соответствующие элементы этих треугольников равны, а именно:
(по I признаку равенства треугольников). Следовательно, все соответствующие элементы этих треугольников равны, а именно:  , ч.т.д.
, ч.т.д.
 и
и  пересекаются в точках
пересекаются в точках  и
и  , причём, точки
, причём, точки 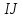 перпендикулярны.
перпендикулярны.









