Решение квадратных уравнений различными способами

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 28

ИНН 2632056869 ОГРН 1022601617829 тел/факс 8(8793) 30-21-00, 30-21-01

г. Пятигорск Ставропольского края, ул. Подстанционная, 23; е-mail: [email protected]

ПРОЕКТ

на тему «Дискриминант. Решение квадратных уравнений различными способами»

(математика)

ученика 8А класса

Ковтун Артема Артемовича

Руководитель проекта:

учитель, математика

Силькунова Ольга Владимировна

г. Пятигорск, 2024

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ……………………………………………………………………..…3

1. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ДИСКРИМИНАНТА...…..………..………5

1. Квадратные уравнения в древнем мире ..……………………..….. …..……5

1.2 Квадратные уравнения в средние века…..………………………………......6

2 РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ СПОСОБАМИ …………………………………………………………….....................................10

2.1 Решение квадратных уравнений дискриминантом …………………….....10

2.2 Теорема Виета….………….………………..………………………………13

2.3 Графический способ решения квадратных уравнений……………………15

2.4 Решения квадратных уравнений по свойствам коэффициента…………..20

ЗАКЛЮЧЕНИЕ………………………………………………………………….22

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ……………………..……..…..23

ВВЕДЕНИЕ

Практически все, что окружает современного человека - это всё так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые достаточно часто сводятся к уравнениям второй степени (квадратным).

На протяжении многих лет людей интересовал вопрос о решении квадратных уравнений. Необходимость решать уравнения второй степени в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. На сегодняшней день одним из простейших способов решений квадратных уравнений является дискриминант. Причина такой популярности: это простота и широкая значимость. Дискриминант является одним из самых узнаваемых понятий школьной математики. В алгебре, обозначаемое буквами D или Δ. Слово “дискриминант” мы слышим при решение квадратных уравнений, в которых обязательна должна присутствовать переменная во второй степени. Однако, в большинстве случаев школьники просто запоминают его формулу и общую формулу для нахождения корней квадратного уравнения. Не зная его историю возникновения и даже определения.

Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением  квадратных  уравнений.  Поэтому каждый ученик должен уметь верно и рационально решать  квадратные уравнения,  это также может мне  пригодится при решении более сложных задач, в том числе и при сдаче экзаменов. Дискриминант имеет огромное значение: она применяется в алгебре буквально на каждом шагу и тот факт, что дискриминант является одним из известнейшим способом решение квадратных уравнений и делает его основной темой моего проекта.

Цель данного индивидуального проекта состоит в рассмотрении формулировки, практического применения, а также история возникновения «Дискриминанта».

Задачи индивидуального проекта включают в себя:

• исследовать историю открытия дискриминанта

• привести формулировки дискриминанта

• определить направления применения

• привести примеры использования дискриминанта при решении квадратных уравнений.

В ходе написания индивидуально проекта использовались следующие методы исследования:

• теоретический анализ изучаемого объекта;

• анализ учебной и научно-популярной литературы;

• сравнительный анализ;

• систематизация данных;

• обобщение информации и формирование выводов.

1.ИСТОРИЯ ВОЗНИКНОВЕНИЯ ДИСКРИМИНАНТА

1.1 Квадратные уравнения в древним мире

Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются неполные и полные квадратные уравнения: X² + X = ¾; X² - X = 14,5 Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, как дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Решением квадратных уравнений занимались и в Древней Греции такие ученые как Диофант, Евклид и Герон. . Герон – греческий математик и инженер впервые в Греции в I век н.э. дает чисто алгебраический способ решения квадратного уравнения

Диофант Диофант Александрийский – древнегреческий математик, живший предположительно в III веке нашей эры. Нередко упоминается как «отец алгебры». Автор книги «Арифметики», посвящённой нахождению положительных рациональных решений неопределённых уравнений. В «Арифметике» Диофанта нет систематического изложения алгебры, но есть ряд задач, сопровождаемых и решаемых при помощи составления уравнений. Вот, к примеру, одна из его задач «Найти два числа, зная, что их сумма равна 20, а произведение — 96».

Мы бы стали решать эту задачу, обозначив за x — одно неизвестное число, (x – 20) — другое, и составив уравнение:

X(X-20)=96

X2-20X-96=0

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как, если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + x, другое же меньше, т.е. 10 – x. Разность между ними 2x. Отсюда уравнение:

(10X+X)(10-X)=96

100-X²=96

X²-4=0

X=2

Тогда одно из искомых 10 + 2 = 12, другое 10 – 2 = 8.

Решение x = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.

В качестве неизвестного Диофант выбирает полуразность искомых чисел, тем самым он упрощает решение, ему удаётся свести задачу к решению неполного квадратного уравнения.

1.2 Квадратные уравнения в средние века.

Занимались решением квадратных уравнений и в Индии. Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:

Ах² + bх = с, а 0. (1)

Задачи часто облекались в стихотворную форму, вот одна задача индийского математика Бхаскары.

Задача

«Обезьянок резвых стая

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавляясь,

А двенадцать по лианам…

Стали прыгать, повисая.

Сколько ж было обезьянок,

Ты скажи мне, в этой стае?»

Бхаскара пишет под видом:

х² - 64х = -768

и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32², получая затем:

х² - 64х + 32² = -768 + 1024

(х - 32)² = 256

х - 32 = 16

х₁ = 16, х₂ = 48.

В период Раннего Средневековья Средняя Азия становится мировым центром наук, подарившим миру многочисленных учёных. К числу знаменитых учёных того времени принадлежит аль-Хорезми Мухаммед бен Муса (полное имя Абу Абдуллах Мухаммед ибн Муса́ аль-Хорезми).  В мировой науке Мухаммед бен Муса известен своим трактатом по математике «О числах и действиях с ними». В этом сочинении впервые дано систематическое изложение арифметики, основанной на десятичной позиционной системе исчисления. И хотя подлинный арабский текст утерян, благодаря переводу его в XII веке с арабского на латинский язык европейские учёные впервые познакомились с индийско-арабским способом счёта. С этого времени «арабские» цифры навсегда вошли в европейскую и мировую математику.

Второй трактат бен Муса – учебник математики, выпущенный им под заглавием «Китаб аль-джебр валь мукабала» около 830 года, посвящён в основном решению уравнений первой и второй степени. Бен Муса подчёркивал, что написал свою книгу, чтобы помочь людям решать их проблемы в повседневной жизни. Он рассматривал такие важные для того времени вопросы, как деление наследства, купеческие счета, судебные дела, торговые сделки и т.д.

Учёный дал классификацию числовых линейных и квадратных уравнений и метод их решения. В алгебраическом трактате Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:

1)  «Квадраты равны корням», т. е. ах² = bх.

2)  «Квадраты равны числу», т. е. ах²= с.

3)  «Корни равны числу», т. е. ах = с.

4)  «Квадраты и числа равны корням», т. е. ах² + с = bх.

5)  «Квадраты и корни равны числу», т. е. ах²+ bх =с.

6)  «Корни и числа равны квадратам», т. е. bх + с == ах².

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-джабр и ал-мукабала. Его решение, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида Аль-Хорезми, как и все математики до XVII в., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений Аль-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.

Формулы решения квадратных уравнений в Европе впервые были изложены в «Книге абака» (1202 г.) итальянским математиком Леонардо Фибоначчи. Эта книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из этой книги переходили почти во все европейские учебники XIV-XVII вв. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду x2 + bх = с при всевозможных комбинациях знаков и коэффициентов b, c, было сформулировано в Европе в 1544 г. М. Штифелем.

Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошёл к введению отрицательных чисел.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета. Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A - A2, равно BD, то A равно В и равно D».

Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D - коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место

(а + b)х - х2 = ab, т.е.

х2 - (а + b)х + аb = 0, то

х1 = а, х2 = b.

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и при решении уравнений рассматривал лишь случаи, когда все корни положительны.

Лишь в XVII в., благодаря трудам Жирара, Декарта, Ньютона и других учёных, способ решения принимает современный вид. Первым, кто написал дискриминант в математическом виде, считается немецкий ученый Иога́нн Карл Фри́дрих  Гаусс. А назвал дискриминант дискриминантом британский математик Джеймс Джозеф Сильвестр в 1851.

Таким образом, квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.

2. Решение квадратных уравнений различными способами

2.1 РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ ДИСКРИМИНАНТОМ

Квадратным уравнением называют уравнение вида ах²+bх+с=0, где коэффициенты а, b, с - любые действительные числа, причем, а≠0. Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.

Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени.

Квадратное уравнение называют приведенным, если старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.

х²+рх+q=0 – стандартный вид приведенного квадратного уравнения

Кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.

Полное квадратное уравнение – это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля.

Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b и с равен нулю.

Решение квадратных уравнений

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо. Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0. Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

Не имеют корней;

Имеют ровно один корень;

Имеют два различных корня.

Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант. Дискриминант:

Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b² − 4ac. Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

Если D

Решим уравнение:

2x²+ x + 1 = 0.

Обозначим коэффициенты: a=2 b=1, c=1. Далее находим дискриминант по формуле: D = b ² –4ac, D = 1 ² – 4 ∗ 2 ∗ 1 = 1 – 8 = − 7 D

Значит, уравнение корней не имеет

Если D = 0, есть ровно один корень:

Решим уравнение: 4x ² + 4x + 1 = 0.

Обозначим коэффициенты: a = 4, b = 4, c = 1. Далее находим дискриминант по формуле: D = b² – 4ac, D = 4² – 4 ⋅ 4 ⋅ 1 = 16 – 16 = 0 D=0 значит, уравнение имеет 1 корень. Находим корень уравнения по следующей формуле: x = − b/2a

Подставляем численные значения: x = − 4 / 2 ⋅ 4 = − 4 / 8 = − 1 / 2 = − 0,5 x

Если D 0, корней будет два:

Решим уравнение: 3 x 2 + 7 x − 6 = 0.

Обозначим коэффициенты: a = 3, b = 7, c = − 6. Далее находим дискриминант по формуле: D = b²– 4ac, D = 7 2 – 4 ∗ 3 ∗ ( − 6 ) = 49 + 72 = 121 = 11² D 0 значит, уравнение имеет 2 корня. Находим корни уравнения по следующим формулам:

x 1 = − b + √ D / 2a

x 2 = (− b − √ D / 2a

Подставляем численные значения:

x 1 = ( − 7 + 11 ) / 2 ∗ 3 = 4 / 6 = 2 /3

​x 2 = ( − 7 – 11 ) / 2 ∗ 3 = − 18 / 6 = − 3

Ответ: (x1 = 2 /3, x2 = − 3)

Если второй коэффициент уравнения четный, можно решать уравнение через k, тогда будет другая формула дискриминанта: D1=k²-ac. Решим уравнение: − x²+ 2x + 8 = 0.

Обозначим коэффициенты: a = − 1, b = 2, c = 8 b – четное. Далее находим дискриминант по формуле: D1 = k ² – ac, D1 = 1 ² – ( − 1 ) ∗ 8 = 1 + 8 = 9 = 3 ²

D1 ​ 0 – значит, уравнение имеет 2 корня. Находим корни уравнения по следующим формулам:

x 1 = ( − k + √ D 1 ) / a

x 2 = ( − k − √ D 1 ) / a

Подставляем численные значения:

x 1 = ( − 1 + 3 ) / ( − 1 ) = 2 / ( − 1 ) = − 2

x 2 = ( − 1 – 3 ) / ( − 1 ) = − 4 / ( − 1 ) = 4

Ответ: x1 = -2, x2 = 4.

2.2 ТЕОРЕМА ВИЕТА

В математике существуют специальные приемы, с которыми многие квадратные уравнения решаются очень быстро и без дискриминантов. Более того, при надлежащей тренировке многие начинают решать квадратные уравнения устно, буквально «с первого взгляда». Мы рассмотрим один из таких приемов — теорему Виета. Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета.

Теорема звучит так: сумма корней приведённого квадратного уравнения x² + bx + c = 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Сумма корней приведенного квадратного трехчлена x²+px+q=0 равна его второму коэффициенту p с противоположным знаком, а произведение - свободному члену q.

x1+x2=−p, x1 x2=q

В случае неприведенного квадратного уравнения ax²+bx+c=0формулы Виета имеют вид:

x1+x2=−b/a, x1 x2=c/a

Значимость теоремы Виета заключается в том, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные многочлены от двух переменных  x1+x2 и  x1 x2  . Теорема Виета позволяет угадывать целые корни квадратного трехчлена.

Пример

Задание. Используя теорему Виета, найти корни уравнения x2−5x+6=0

Решение. Согласно теореме Виета, имеем, что

x1+x2=5

x1x2=6

Подбираем значения x1x1 и x2x2, которые удовлетворяют этим равенствам. Легко видеть, что им удовлетворяют значения

x1=2 и x2=3

Ответ. Корни уравнения x1=2,x2=3

Обратная теорема Виета

Если числа x1 и x2 удовлетворяют соотношениям x1+x2=−p, x1x2=q, то они удовлетворяют квадратному уравнению x2+px+q=0,то есть являются его корнями.

Пример

Задание. Зная, что числа x1=3и x2=−1- корни некоторого квадратного уравнения, составить само это уравнение.

Решение. Пусть искомое квадратное уравнение имеет вид:

x2+px+q=0

Тогда, согласно теореме Виета, его коэффициенты связаны с корнями следующими соотношениями:

x1+x2=−p, x1x2=q

Тогда

p=−(x1+x2)=−(3+(−1))=−2

q=x1x2=3⋅(−1)=−3

То есть искомое уравнение

x2−2x−3=0

2.3 ГРАФИЧЕСКИЙ СПОСОБ РЕЩЕНИЯ КВАДРТАНЫХ УРАВНЕНИЙ

Первый способ

Построим график функции x2−2x−8=0.

1. Имеем: a=1, b=−2, x0=−b2a=1,y0=f(1)=12−2−8=−9. Значит, вершиной параболы служит точка (1;−9), а осью параболы является прямая x=1.

2. Возьмём на оси x две точки, симметричные относительно оси параболы, например, точки x=−2 и x=4. Имеем f(−2)=f(4)=0. Построим на координатной плоскости точки (−2;0) и (4;0).

3. Построим параболу по точкам (−2;0), (1;−9), (4;0).

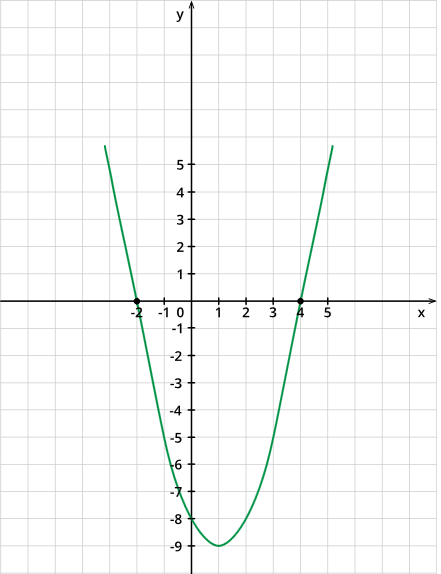
Корни уравнения x2−2x−8=0 — это первые координаты точек, в которых функция равна нулю (то есть в которых график пересекает ось х); поэтому имеем решение: x1=−2;x2=4.

Второй  способ

Запишем уравнение в другом виде x2=2x+8.Рассмотрим функции в  левой и правой частях уравнения y=x2;y=2x+8. В одной системе координат построим их графики и найдём точки пересечения графиков:

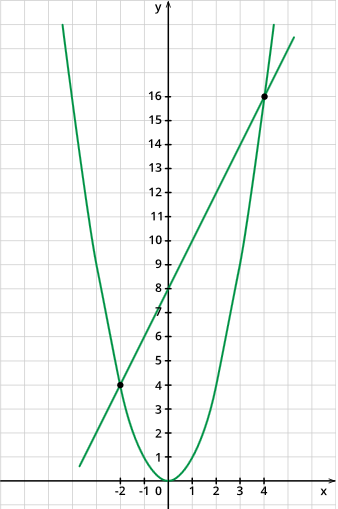
Получили две точки:: C(−2;4) и D(4;16). Решением уравнения будут первые координаты точек C и D, имеем: x1=−2;x2=4.

Третий способ

Преобразуем уравнение к виду x2−8=2x. Построим в одной системе координат графики функций: y=x2−8;y=2x и определим точки их пересечения:

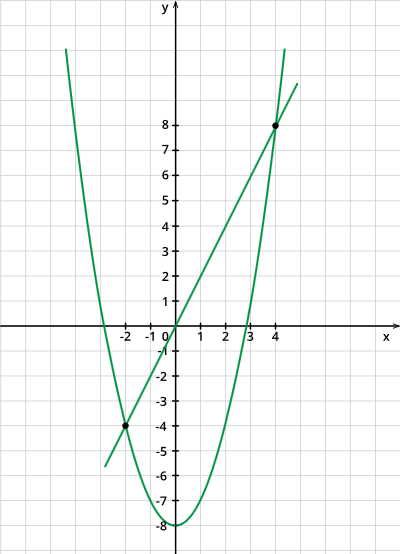
Получили две точки: C(−2;−4) и D(4;8). Решением уравнения будут первые координаты точек C и D, то есть x1=−2;x2=4.

Четвёртый способ

Преобразуем уравнение к виду x2−2x+1−9=0 и далее x2−2x+1=9→(x−1)2=9.
Построим в одной системе координат параболу y=(x−1)2, прямую y=9 и определим точки их пересечения:

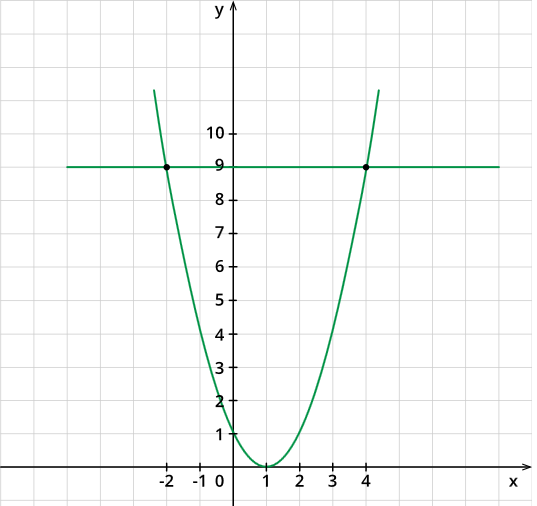
Получили две точки: C(−2;9) и D(4;9). Решением уравнения будут первые координаты точек C и D, поэтому x1=−2;x2=4.

Пятый способ

Так как x=0 не является корнем уравнения, то разделим левую и правую части на x:

x−2−8x=0;x−2=8x.

Рассмотрим функции в  левой и правой частях уравнения y=8x, y=x−2 и определим точки их пересечения:

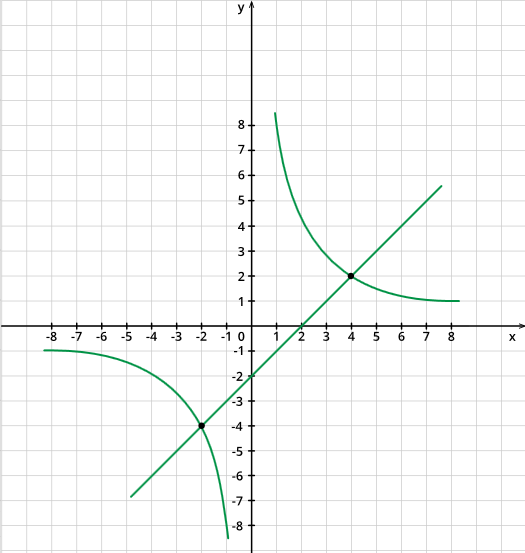
Получили две точки: A(−2;−4) и B(4;2). Решением уравнения будут первые координаты точек A и B, следовательно, x1=−2;x2=4.

2.4 Решения квадратных уравнений по свойствам коэффициента

Свойство 1

Дано квадратное уравнение ax² + bx + c = 0. Если          a + b + c = 0 (сумма коэффициентов), то

x₁ = 1, x₂ = c/a

х² + х – 2 = 0;

а = 1, в = 1, с = -2.

Так как 1+1–2 =0, то х₁ =1, х₂ = -2.

Свойство 2

Дано квадратное уравнение ax² + bx + c = 0. Если          a - b + c = 0 (сумма коэффициентов), когда b взято с противоположным знаком или a + c = b, то 

x₁ = -1, x₂ = -c/a

341x² + 290x - 51 = 0

        Решение:

        Здесь, a = 341, b = 290, c = -51

 Проверим удовлетворяют ли коэффициенты условию  свойства    

       341 - 51 = 290. Получим а + с = b.

Следовательно, мы   можем воспользоваться свойством 2.

x₁ = -1 и х₂ = 51/341

        Ответ: -1; 51/341

Свойство 3

Если в квадратном уравнении ax² + bx + c = 0. Коэффициент b представлен в виде 2k, т.е. является четным числом, то формулу корней уравнения можно переписать в более простом виде

D = (b/2)2 + a*c

  3x² + 2,2x - 0,16 = 0

        Решение:

        Коэффициент b = 2,2 

        D = 1,1² + 3 * (-0,16) = 1,69

x_1,2 = (-1,1 ± 1,3)/3   

Заключение

Человечество прошло длительный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание все более полным и совершенным.

В ходе выполнения проектной работы мы считаем, что с поставленными целями и задачами справились, нам удалось обобщить и систематизировать изученный материал по выше указанной теме.

Способов решения квадратных уравнений очень много. Мы нашли основные способы решения квадратных уравнений. Нужно отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на экзаменах. Для того чтобы усвоить все методы решения уравнений, нужно прорешать несколько уравнений изучаемым способом. В данной работе, не представлены тренировочные задания для каждого из способов решения квадратных уравнений.

Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в математике. Эти знания могут пригодиться нам на протяжении всей жизни, а так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должны заинтересовать увлекающихся математикой.

Литература

1. Глейзер, Г.И. История математики в школе/ Г.И. Глейзер.-М.: Просвещение, 1982- 340с.

2. Гусев, В.А. Математика. Справочные материалы/ В.А. Гусев, А.Г. Мордкович - М.: Просвещение, 1988, 372с.

3. Брадис, В.М. Четырехзначные математические таблицы для средней школы/ В.М, Брадис-М.: Просвещение, 1990-

4. Теорема Виета– Режим доступа:.http://phizmat.org.ua/2009-10-27-13-31-30/817-stihi-o-fransua-vieta/ Теорема Виета(ресурсы удаленного доступа (Internet)). 10.12.2013.

5. Квадратные уравнения– Режим доступа: http://revolution.allbest.ru/pedagogics/00249255_0.html(ресурсы удаленного доступа (Internet)). 10.01.2014.

27