576
90 451 
© 2021, Прилагаева Ольга Владимировна 203 0
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Решение неравенства второй степени.
Категория:
Алгебра
28.12.2021 08:27
Просмотр содержимого документа
«Решение неравенства второй степени.»
Алгебра 9 кл
Урок № 40
Тема урока : Решение неравенств второй степени
Цель урока: ввести понятие неравенств второй степени с одной переменной, дать определение
-познакомить с алгоритмом решения неравенств на основе свойств квадратичной функции
-сформировать умение решать неравенства второй степени с помощью графика квадратичной функции
Ход урока
Организационный этап.
Повторяем § 6 п.14 .Решить №315 ,№ 312(а,г)
. Сократите дробь (задание даётся выборочно)
а) 
; б) 
.
Р е ш е н и е
а) 
Упростите выражение:
а) 
;
б) 
.
Р е ш е н и е
а) 
б) 
Если останется время, то можно предложить учащимся задание на построение графика функции 
.
Р е ш е н и е
Данная функция не является элементарной, и по точкам ее строить неудобно. Сократим дробь, задающую функцию:
Таким образом, график исходной функции совпадает с графиком функции у = х – 4, но точка х = 2 не входит в область определения данной функции, поэтому на графике эта точка будет выколотой.
Фронтальный опрос.
Какой вид имеет неравенство второй степени с одной переменной? (Неравенства вида ах2 + вх + с 0 и ах2 + вх + с ).
Что такое а, в, с?
Какие ограничения для коэффициента а? (а≠0)
3.Актуализация опорных знаний
Что значит решить неравенство? (Решить неравенство – значит найти все его решения или док Выберите из данных неравенств неравенства второй степени с одной переменной.
х2 + 2х – 48
2) (х – 1)(х – 2) ≥ 0
3) х2 – 6 ≤ 0
4) 7х + 2 х2 4
5) х – 3 0
6) – 20 х2 ≤ 5
2.Изучение нового материала(учебник § 6 п.15 Решить №325(а,б )
Изучить § 6п.14.Решить, №306 (а-г),315,320(а,б),332
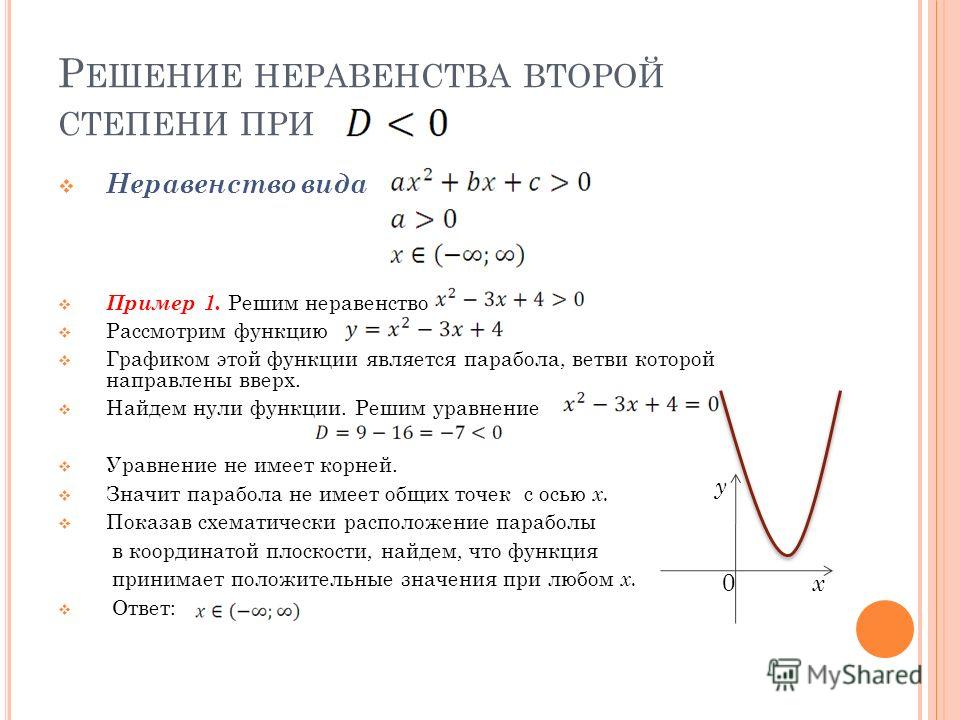
Алгоритм решения неравенств:
1. находим дискриминант квадратного трехчлена и выясняем, имеет ли трехчлен корни.
2. если имеет – корни отмечают на оси х и через точки проводят схематически параболу, учитывая направление ветвей (а0 – ветви вверх, aa0) или в нижней (a
3. находят промежутки, для которых точки параболы расположены выше или ниже оси х.
Физминутку делаем обязательно, не забываем в любое время.
Домашняя работа : Изучить §6 п. 15 . Решить №327(б,в ) , № 333,№ 337 (а,б).
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
