Практико-значимая работа
«Решение параметрических уравнений.
Доказательство тождеств»
МБОУ «Коробовский лицей»
Родина А.И
2019г
Решение уравнения – задача по нахождению таких значений аргументов, при которых это равенство достигается. Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет [Википедия].
§1. Уравнения , содержащие параметр.
ПРИМЕР 1. Решите уравнение
a2 (
x 1) 6
x (5
x 2)
a . После преобразований данное уравнение примет вид: (
a 2)(
a 3
)x
a(
a 2) . Для того, чтобы выразить х нужно будет поделить а(а-2) на (а-2)(а-3). Но выполнение этой операции возможно не всегда (делить на нуль нельзя). Все выше сказанное определяет дальнейший ход рассуждений: исследовать случаи, когда коэффициент при х равен нулю и когда – отличен от нуля. Если
а = 2, то уравнение примет вид 0
х=0. Решением полученного уравнения является любое действительное число. Если
а = 3, то уравнение примет вид 0
х = 3
. Решений нет. Если
a 2 и
a 3, то х=(а(а-2))/(а-2)(а-3)=а/(а-3) Ответ: при
а = 2
x
R ; при
а = 3 решений нет; при
a 2 и
a 3 х=а/(а-3) ПРИМЕР 2
. Найти все а, при каждом из которых уравнение ln(xa2+xa+2x−x3)=ln(2x−x2) имеет ровно один корень.
Решение Итак, т.к стоит логарифм, то обязательно пишем ОДЗ (можно написать на одну из двух функций), убираем логарифмы и получаем систему xa2+xa+2x−x3−2x+x2=0 (1) 2x−x20 (2) Решением второго будет x∈(0;2) Разберемся с первым (1) x(a2+a−x2+x)=0 x2−a2−(a+x)=0 (x−a)(x+a)−(x+a)=0 (x−a−1)(x+a)=0 Мы получаем два корня уже. Но нужен один, поэтому рассматриваем два случая, когда один корень подходит под ОДЗ, а второй нет. 1) x=−a и при этом −a∈(0;2) x=a+1 и при этом a+1∉(0;2) Решим ее −2 Получаем что a∈(−2;1] причем 1 входит в решение, в этом можно убедится подстановкой и получить один корень 2) x=−a и при этом −a∉(0;2) x=a+1 и при этом a+1∈(0;2) Решая аналогично получаем, что a∈[0;1) 3) Когда корни совпадают То есть a+1=−a и отсюда a=−0.5 Ответ: a∈[0;1) и a∈(−2;1] {0.5}
ПРИМЕР 3. При каких значениях параметра уравнение x^4-8x^3-2x^2+24x+a=0 имеет ровно 3 различных корня?
Решение Преобразуем
(x−2)4=26x2−56x+16−a Построим график функции
y=(x−2)4 и будем строить параболу в зависимости от а
y=26x2−56x+16−a Графики будут пересекаться в трех точках в том случае, когда они пересекаются в двух точках и касаются друг друга. Рассмотрим функцию
g(x)=26x2−56x+16−a . Найдем их производные функций:
y′=4(x−2)3
g′(x)=26∗2x−26 Пусть
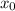
— абсцисса точки касания двух графиков, тогда
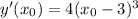
и
g′(x)=26∗2x0−56. Приравнивая функции, получим Произведение равно нулю в том случае, когда хотя бы один из множителей равен нулю
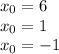
Найдем теперь ординату точку касания
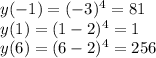
Подставим координаты
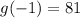
и
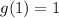
и
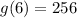
, мы получим Но при а = 360 графики пересекаются в одной точке. То есть, при а = -15 и а = 17 данное уравнение имеет три различных корня.
Ответ: a = -15 и a = 17. ПРИМЕР 4. Найдите все значения
а, при каждом из которых уравнение 3
x4
– 6
х2
– а = 0 имеет ровно один корень на промежутке (-1; 2).
Приведем уравнение к виду 3x4–6х2=а. Исследуем функцию у=3x4–6х2.
у12x3 12х; у0 при х=0 или х=1. При этом у(0)=0, у(-1)=-3, у(1)=-3
На координатной плоскости изобразим график функции у=3x4–6х2,
где х(1; 2). Заметим, что у(2)=24.

По графику видим, что уравнение 3x4–6х2=а имеет ровно один корень
при а=-3 или 0a
Ответ: а=-3, 0a
ПРИМЕР 5.
Найдите все значения
а, при каждом из которых функция
f (
x)
x3 3
ax2 3
a2
x 3
x 1 имеет ровно один экстремум на промежутке (0;3].
f (x) 3x2 6ax3a2 3. f (x) 0 при х=а-1 или х=а+1. Очевидно, что обе
найденные точки будут являться точками экстремума данной функции.
Выясним, при каких значениях а только одна из них попадает в про-
межуток (0;3].
0a 13, 1a 4. 2) 0 a 13, - 1a 2 .

Видим, что искомые значения 1a 1, 2 a 4 (одна штриховка).
Ответ: 1a 1, 2 a 4
ПРИМЕР 6.



Пример7. 





Пример 8. 



§2. Доказательство тождеств.
Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят.
Пример 1.
Докажите тождество x*(a+b) + a*(b-x) = b*(a+x).
Решение.
Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.
Имеем,
Приведем подобные слагаемые и вынесем общий множитель за скобку.
Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.
Пример 2.
Докажите тождество a^2 + 7*a + 10 = (a+5)*(a+2).
Решение.
В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.
Получим,
Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.
Способы доказательства тождеств Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным. Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным. Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным. Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
12





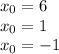 Найдем теперь ординату точку касания
Найдем теперь ординату точку касания 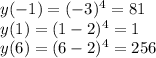 Подставим координаты
Подставим координаты 






















