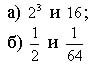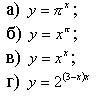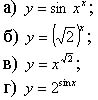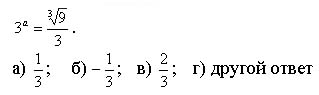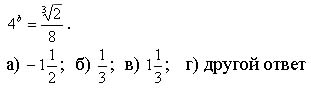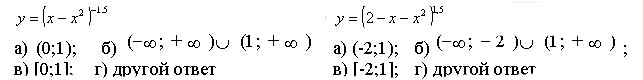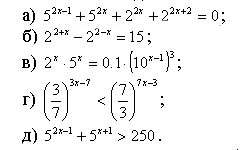Тема урока:
"Решение показательных уравнений и неравенств"
Девиз урока:
«Реши сам – помоги товарищу!»

План
1. Организационный момент урока.
2. Актуализация знаний.
а) Проверка домашнего задания при помощи кодоскопа.
б) Индивидуальная работа по карточкам (2 человека):
в) Групповая работа (работу оценивают консультанты).
3. Разминка.
4. Математический диктант (I - II варианты).
5. Беседа с классом.
6. Историческая минутка.
7. Закрепление изученного материала.
Работа в тетрадях:
| Решить уравнения: 1. 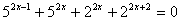 2. 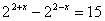 3. 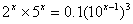 | Решить неравенства: 1.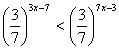 2. 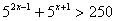 |
Решить графически (на миллиметровой бумаге):
| I вариант
1. 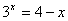 | II вариант
1. 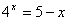 |
8. Подведение итогов урока.
9. Выставление оценок.
10. Постановка домашнего задания.
| Решить неравенства:
а) 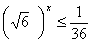 б) 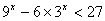 | Решить уравнения: а)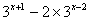 б)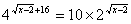 |
| Индивидуальные задания из КИМов ЕГЭ по карточкам. |
План - конспект урока
Цели и задачи урока:
образовательные: создавать ситуацию успеха, в ходе которой учащиеся актуализируют свои знания по теме и приобретут новые. Формировать умение решать показательные уравнения и неравенства, используя алгоритм решения на основе свойств показательной функции; создавать организационные и содержательные условия, при которых учащиеся открывают и осваивают алгоритм, становятся субъектом деятельности, учатся критически оценивать свои знания, формируют эмоционально - ценностное отношение к своей учебной деятельности;
развивающие: вырабатывать умения анализировать и систематизировать изученный материал, выделять главное, сравнивать, обобщать знания по теме, сознательно воспринимать учебный материал; развивать умения самостоятельно приобретать новые знания, использовать для достижения поставленной задачи полученные знания;
воспитательные: вырабатывать математически грамотную речь, чувство ответственности, культуру диалога, приучать к эстетическому оформлению записи в тетради и на доске, умению выступать перед аудиторией и выслушивать других, умению общаться, прививать навыки самостоятельной работы и самостоятельного выбора вида деятельности, способствовать развитию у учащихся навыков взаимоконтроля и самоконтроля знаний.
Девиз урока: «Реши сам – помоги товарищу!».
Формы работы учащихся: фронтальная, индивидуальная, в группе.
Оборудование: таблицы, кодоскоп, карточки-задания, карточки-подсказки, план урока - на каждой парте.
Ход урока
Организационный момент.
Актуализация знаний.
а) Проверка домашнего задания.
Проверка осуществляется с помощью кодоскопа. Домашнее задание готовится на пленке учащимся и проецируется через кодоскоп. Все учащиеся сверяют свои решения и при необходимости вносят коррективы в решение.
I. Вычислить:
а) 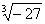 ; б)
; б) 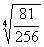 ; в)
; в) 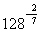 ; г)
; г) 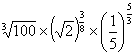 .
.
II. а) Решить уравнения:

б) Решить неравенства:

б) Индивидуальная работа по карточкам.
| Карточка № 1 1) Сформулируйте определение степени числа 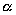 с натуральным показателем n. с натуральным показателем n. 2) Найти значение выражения: 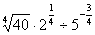 . . 3) Решить уравнение: 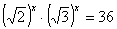 . .
| Карточка № 2 1. Сформулируйте определение степени числа 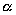 с натуральным показателем n. с натуральным показателем n.
2. Сравнить числа: 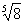 и и 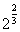 . . 3. Решить неравенство: 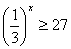 . .
|
в) Групповая работа
(консультант работает с группой учащихся, которые выполняют работу по индивидуальным карточкам, и оценивает их работу).
- Сегодня мы продолжим учиться решать показательные уравнения и неравенства и попытаемся успешно справиться с заданиями. Эта тема очень важна, она является ступенькой для дальнейшего обучения. Благодаря полученным умениям и навыкам, мы сможем успешно сдать ЕГЭ, а также сможем решать задачи практической направленности.
- Математику не зря называют “царицей наук”, ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики – любознательность. Постараемся доказать это на уроке. Вы уже умеете решать показательные уравнения и неравенства. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке.
- Сейчас мы будем работать в группах и каждый этап урока зафиксируем в рабочей карте. Вашу работу на каждом этапе урока оценивает консультант. Рабочая карта урока:
| Фами-лия и имя учаще-гося | Проверка домашней
работы | Работа
по карточкам
(по алгоритму) | Работа
в группах | Устная работа | Матема-
тический диктант | Доклад | Добы-вай знания сам | Итог урока |
|
|
|
|
|
|
|
|
|
|
Работа по карточкам:
1 карточка
Решить уравнение: 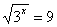 .
.
Решить графически неравенство: 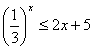 .
.
Свойства показательной функции.
2 карточка
3 карточка
3. Устная работа.
1. Приведите степени к одному основанию:
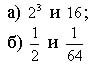
2. Представить в виде корня из числа выражений:
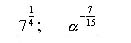

4. Математический диктант.
(Самопроверка через кодоскоп, выставление оценок).
Диктант пишется на листочках под копирку. Задание готовится заранее с ответами на табличках.
1 экземпляр сдается учителю.
2 экземпляр проверяют сами учащиеся.
| I вариант | II вариант |
| 1. Какая из данных функций является показательной: |
| 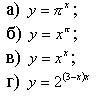
| 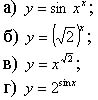
|
| 2. При каких значениях а верно равенство 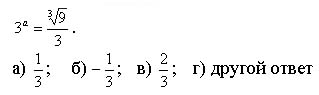 |
2. При каких значениях b верно равенство 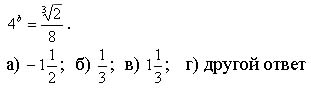
|
| 3. Найдите наибольшее целое решение неравенства: |
| 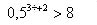
| 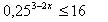
|
| а) -2; б) -3; в) -4; г) 3 | а) 2; б) 3; в) -2; г) -3 |
| 4. Найдите сумму корней уравнения: |
| 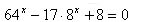
| 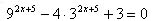
|
| 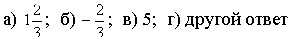
| а) -4,5; б) 5; в) 4,5; г) другой ответ |
| 5. Найдите область определения функции |
| 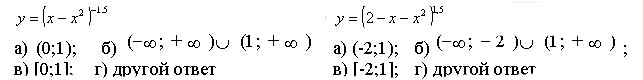
|
Норма оценок: «5» - 5 заданий; «4» - 4 задания; «3» - 3 задания; «2» - 2, 1, 0 заданий.
5. Беседа с классом.
Какое уравнение называется показательным?
(Уравнение вида 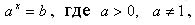 , где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому виду, называется показательным.)
, где а – положительное число, отличное от 1, и уравнения, сводящиеся к этому виду, называется показательным.)
На какой теореме основано решение показательных уравнений?
(Если 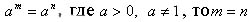 ).
).
Назовите основные методы решения показательных уравнений.
( а) Метод введения новой переменной.
б) Вынесение за скобки общего множителя.
в) Приведение показательного уравнения к квадратичному:
(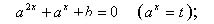 );
);
г) Функционально-графический метод, который основан на использовании графических иллюстраций или каких-либо свойств функции.
д) Метод уравнивания показателей, который основан на теореме о том, что если
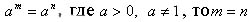 .
.
е) Рассказать о свойствах показательной функции.
6. Историческая минутка.
Учащийся зачитывает приготовленный доклад.
Учитель и учащийся рассказывают о показательной функции, показательных уравнениях и неравенствах.
Сегодня мы дополнили знания о показательной функции, о ее применении в различных областях жизнедеятельности человека, и сейчас на уроке мы продолжим работу по решению показательных уравнений и неравенств.
7. Закрепление изученного материала.
В.Г. Белинский говорил: «Без стремления к новому нет жизни, нет развития, нет прогресса». Мы будем руководствоваться этими словами в своей работе на уроке.
На доске записаны уравнения и неравенства (у школьников эти уравнения записаны в плане урока, который лежит на каждой парте). Учащиеся выполняют задания на доске и в тетрадях.
№ 1. Решите уравнения и неравенства:
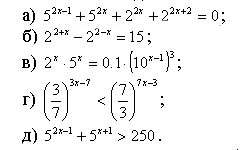
№ 2. Решить графически (учащиеся выполняют самостоятельно при помощи таблицы-подсказки, на миллиметровой бумаге и сдают на проверку учителю).
I вариант. 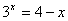
II вариант. 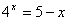
Проверку делают при помощи кодоскопа, каждый ученик видит свою ошибку и может заранее оценить свою работу.
8. Подведение итогов урока.
Учащиеся подводят сами. Участники группы оценивают степень участия каждого ученика в решении уравнений и неравенств, и выставляют им оценки в рабочую карту урока. Итоговую оценку в рабочей карте выставляет учитель.
9. Выставление оценок
Каждый ученик получил по две оценки, а те школьники, которые отвечали у доски и по карточкам, выполняли домашнее задание - по три оценки.
10. Домашнее задание
Домашнее задание записано в начале плана урока.
В конце урока учитель предлагает ученикам взять листик в форме снежинки и, если учащийся уходит с урока в хорошем настроении, приклеить его на заранее подготовленный (нарисованный) ствол ели. В результате получилось нарядное вечнозеленое дерево.
Анализ усвоения материала урока учащимися
11 класс изучает математику по программе профильного уровня. В классе 17 учеников, из них условно можно выделить 3 группы: высокий, средний и низкий уровень развития и учебных возможностей.
У восьми учащихся высокий уровень, они умеют анализировать, сравнивать, обобщать. Эти учащиеся работоспособны, умеют отстаивать свою точку зрения, объективно оценивать себя, самоорганизованы и замотивированы. Шесть учеников могут работать на продвинутом уровне, но степень самостоятельности низкая. Трем учащимся с трудом дается материал базового уровня, у них низкая работоспособность, имеются пробелы в знаниях, не всегда могут выполнять задания по образцу.
Исходя из характеристики учебных возможностей учащихся, был выбран именно такой замысел урока, как самостоятельный выбор уровня заданий, опорные карточки с алгоритмом решения показательных уравнений и неравенств, для третьей группы, что создает комфортные условия изучения материала и составляет здоровьесберегающий компонент урока.
Специфика урока заключается в самостоятельном определении личных целей и задач в изучении материала. Преобладающий метод - познавательный, через самостоятельную деятельность. При такой организации урока учащиеся несут ответственность за выполнение заданий, самостоятельно определяют уровень заданий на урок, т.к. у них есть возможность перейти на более высокий уровень знаний. Они учатся формулировать вопросы не типа «Я не могла (не мог…)…», а «Я решаю, но сомневаюсь так или нет…» и т.д., определять самому себе объем, уровень заданий, ищут методы.
Урок организован таким образом, что каждый учащийся, выполняя деятельность на уроке самостоятельно, может рассчитывать на помощь учителя, подсказку в виде опорной карточки, образца, которыми может пользоваться и при выполнении домашнего задания. С интересом учащиеся относятся к заданиям из банка задач к ЕГЭ.





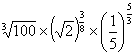 .
.
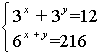 .
.