Введение
Значительная часть специальностей, для поступления на которые требуется математика профильного уровня, носит практико ориентированную, в том числе экономическую направленность. В связи с этим с 2015 года в КИМ ЕГЭ по математике профильного уровня введена практико ориентированная задача повышенного уровня сложности, за решение которой установлен максимальный первичный балл 2. Текстовая задача проверяет применение знаний в практической деятельности и повседневной жизни, умение строить и исследовать математические модели.
В открытом банке заданий ФИПИ содержатся данные задачи трех сюжетных линий: задачи на кредиты, задачи на вклады и задачи на оптимальный выбор. Статистика выполнения данного задания следующая:
| год | % учащихся, получивших ненулевые баллы | % учащихся, получивших максимальный балл |
| 2015 | 12 | 6,5 |
| 2016 | 13 | 7,8 |
| 2017 | 14,8 | 8,6 |
| 2018 | 2,2 | Нет данных |
Многие учащиеся без предварительной подготовки не могут решать задачи с экономическим содержанием, поэтому задача учителя помочь учащимся овладеть приемлемыми для них способами решения данных задач.
Для этого необходимо познакомить учащихся с понятиями банк, банковские услуги, кредиты и вклады (депозиты).
Целью данной разработки является рассмотрение главных функций банков:
— кредитование и его основные принципы, различные схемы погашения кредитов, расчет платежей;
— накопление денежных средств, различные схемы начисления процентов.
Задачей данной разработки является умение применять учащимися полученные знания для решения практико-ориентированных задач в ГИА по математике в 11 классе.
Кредит – это экономические отношения, связанные с передачей одной стороной другой каких-либо материальных ценностей (денег, товара) при выполнении следующих условий: возвратности заемных средств в установленный срок за определенную плату.
Существует 2 способа погашения кредита:
-
Выплата суммы долга одинаковыми платежами. Эта схема называется аннуитетным графиком платежа;
-
Выплата суммы долга по принципу убывания, т. е. в начале срока погашения сумма наибольшая, а к концу – наименьшая. Принцип таков: долг по кредиту делится на равные части, а проценты начисляются на остаток платежа. Такой график погашения называется дифференцированным.
Кроме этого существуют индивидуальные схемы погашения кредитов.
Депозит (или как его ещё называют — банковский вклад) — это определённая сумма денежных средств, которая передаётся каким-либо лицом кредитному учреждению (например, банку).
Цель передачи денежных средств — получить какой-либо доход (обычно в виде процентов), который образуется в результате проведения тех либо иных финансовых операций с денежными средствами.
Все проценты на общую сумму банковского депозита начисляют со дня, который следует за днём поступления депозита в банковское учреждение. Начисление происходит до того дня, когда сумма будет возвращена вкладчику или же до дня, когда банковский депозит будет закрыт самим вкладчиком.
Обычно вкладчик имеет право по распоряжению своими же процентами. Вкладчик имеет возможность изъять проценты по истечению периода выплаты всех процентов, которые были заранее указаны в договоре, или присоединить проценты ко всей сумме банковского депозита. Присоединение процентов к общей сумме депозита называется капитализацией процентов. Капитализация процентов позволяет (в некоторых случаях, когда речь идёт о высокой процентной ставке) существенно увеличить всю сумму вклада, по которой и начисляют оставшиеся проценты.
Задачи на кредиты
При решении задач на кредиты рекомендую заполнять следующую таблицу
| Период | Сумма долга на начало периода | Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | rS |
|
|
|
| п |
|
|
|
|
|
| Итого | _____________ |
| S |
| _____________ |
В задачах на кредиты введены следующие переменные:
S – сумма кредита;
r – проценты, выраженные в десятичной дроби;
n – количество периодов (выплат по кредиту, срок кредитования).
Задачи на дифференцированные платежи
При решении данных задач используется формула суммы арифметической прогрессии. На дифференцированные платежи существует четыре типа задач:
– нахождение общей суммы выплат;
– нахождение процента по кредиту;
– нахождение количества выплат (периодов, срока кредитования).
– нахождение суммы кредита.
Задача 1. Нахождение общей суммы выплат.
В июле планируется взять кредит 13 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: каждый январь долг возрастет на 20% по сравнению с концом предыдущего года; в июле каждого года необходимо выплатить часть долга; в конце июля каждого года долг должен быть на одну и ту же сумму меньше долга по сравнению с концом предыдущего года. Чему равна общая сумма выплат после полного погашения кредита, если наименьший годовой платеж равен 1,56 млн рублей?
Решение:
Заполним таблицу по данным задачи
| Период | Сумма долга на начало периода | Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 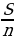
| Sr+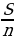 | 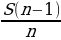
|
| п | 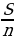
| 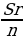
| 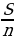
| 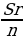 + +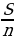
| 0 |
| Итого | ________ | (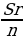 +Sr) +Sr)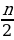 = = 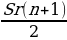 | S | 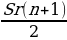 +s +s
| ________ |
Найдем n из строки 1:
13*0,2+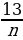 =1,56 n=10 (кредит взят на 10 лет)
=1,56 n=10 (кредит взят на 10 лет)
Найдем сумму платежей из строки Итого:
13*0,2*11/2+13=27,3 млн руб.
Ответ: 27,3 млн руб.
Задача 2. Нахождение процента по кредиту.
15-го января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы: 1-го числа каждого месяца долг возрастет на r% по сравнению с концом предыдущего месяца; со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 24% больше суммы, взятой в кредит. Найдите r.
Решение:
Заполним таблицу по данным задачи:
| Период | Сумма долга на начало периода | Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 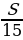
| Sr+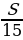 | 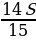
|
| 15 | 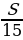
| 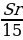
| 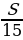
| 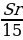 + +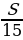
| 0 |
| Итого | ________ | (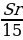 +Sr) +Sr)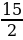 = 8Sr = 8Sr | S | 1,24S | ________ |
Составим уравнение по данным таблицы:
8Sr+S=1,24S
8r=0,24
r=0,03
Ответ: 3%
Задача 3. Нахождение количества выплат (периодов).
В июле планируется взять кредит в банке на сумму 16 млн рублей
на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Решение:
Заполним таблицу по данным задачи:
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 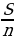
| Sr+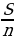 | 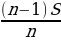
|
| n | 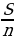
| 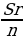
| 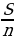
| 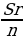 + +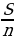
| 0 |
| Итого | ________ | (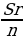 +Sr) +Sr)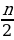 | S | 38 | ________ |
Составим уравнение по данным таблицы:
(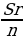 +Sr)
+Sr)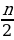 + S=38, подставим в уравнение S и r
+ S=38, подставим в уравнение S и r
(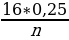 +16*0,25)
+16*0,25)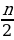 + 16=38
+ 16=38
(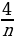 +4)
+4)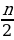 + 16=38
+ 16=38
2+2n =22
п=10(лет)
Ответ: 10 лет.
Задача 4. Нахождение суммы кредита.
15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн рублей?
Решение: Заполним таблицу по данным задачи:
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 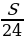
| Sr+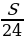 | 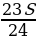
|
| 24 | 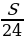
| 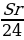
| 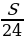
| 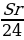 + +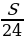
| 0 |
| Итого | ________ | (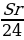 +Sr) +Sr)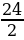 = =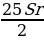 | S | 1 | ________ |
Составим уравнение по данным таблицы:
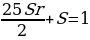 1,25S=1
1,25S=1
S=0,8 (млн руб.)
Ответ: 0,8 млн руб.
Задачи на аннуитетные платежи
При решении данных задач используется формула суммы геометрической прогрессии. На аннуитетные платежи существует четыре типа задач:
– нахождение общей суммы выплат (размера одного платежа);
– нахождение процента по кредиту;
– нахождение количества выплат (периодов, срока кредитования);
– нахождение суммы кредита.
Задача 1. Нахождение общей суммы выплат.
В июле 2020 года планируется взять кредит в банке на сумму 419 375 рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?
Решение:
Заполним таблицу по данным задачи:
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | x- Sr | x | S(1+r)- x |
| 2 | S(1+r)- x | Sr(1+r)- xr | (1+r)( x- Sr) | x | S(1+r)²- x(r+2) |
| 3 | S(1+r)²- x(r+2) | Sr(1+r)²- xr(r+2) | (1+r)²( x- Sr) | x | S(1+r)³- x((x+1)(r+2)+1) |
| 4 | S(1+r)³- x((x+1)(r+2)+1) | Sr(1+r)³- xr((x+1)(r+2)+1) | (1+r)³( x- Sr) | x | 0 |
| Итого | ________ |
| 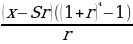
| 4x | ________ |
Составим уравнение по данным таблицы:
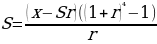
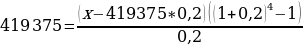
419 375 = (х- 83875)* 5,368
5,368х=450241+419375
5,368х=869616
х=162000 (руб.) – ежегодная выплата
4*162000=648000 (руб.) – общая сумма выплат.
Ответ: 648000 руб.
Задача 2. Нахождение суммы кредита.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года) и банку будет выплачено 292 820 рублей?
Решение: Заполним таблицу по данным задачи:
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | x- Sr | x | S(1+r)- x |
| 2 | S(1+r)- x | Sr(1+r)- xr | (1+r)( x- Sr) | x | S(1+r)²- x(r+2) |
| 3 | S(1+r)²- x(r+2) | Sr(1+r)²- xr(r+2) | (1+r)²( x- Sr) | x | S(1+r)³- x((x+1)(r+2)+1) |
| 4 | S(1+r)³- x((x+1)(r+2)+1) | Sr(1+r)³- xr((x+1)(r+2)+1) | (1+r)³( x- Sr) | x | 0 |
| Итого | ________ |
| 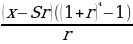
| 292 820 | ________ |
Составим уравнение по данным таблицы:
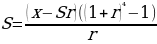
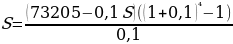
S= 339744,405-0,4641S
1,4641S=339744,405
S= 232050 (руб.) – сумма кредита.
Ответ: 232050 руб.
Задача 3. Нахождение количества выплат.
Максим хочет взять в банке кредит 1,5 миллиона рублей. Погашение кредита происходит раз в год равными платежами (кроме, может быть, последней) после начисления процентов. Процентная ставка 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?
Решение:
Заполним таблицу по данным задачи:
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | x- Sr | x | S(1+r)- x |
| 2 | S(1+r)- x | Sr(1+r)- xr | (1+r)( x- Sr) | x | S(1+r)²- x(r+2) |
| 3 | S(1+r)²- x(r+2) | Sr(1+r)²- xr(r+2) | (1+r)²( x- Sr) | x |
|
| n |
|
|
| х | 0 |
| Итого | ________ |
| 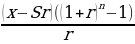
| пх | ________ |
Составим неравенство по данным таблицы:
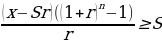
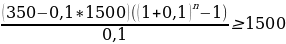
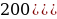
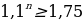 n≥
n≥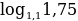 n=6 (лет)
n=6 (лет)
Ответ: 6 лет.
Задача 4. Нахождение процента по кредиту.
В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.
Решение: Заполним таблицы по данным задачи:
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 106964- Sr | 106964 | S(1+r)- 106964 |
| 2 | S(1+r)- 106964 | Sr(1+r)- 106964r | (1+r)( 106964- Sr) | 106964 | 0 |
| Итого | ________ | Sr(2+r)-106964r | (2+r)(106964-Sr)=
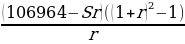 | 213928 | ________ |
| Период | Сумма долга на начало периода |
Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 58564- Sr | 58564 | S(1+r)- 58564 |
| 2 | S(1+r)- 58564 | Sr(1+r)- 58564r | (1+r)( 58564- Sr) | 58564 | S(1+r)²- 58564 (r+2) |
| 3 | S(1+r)²- 58564 (r+2) | Sr(1+r)²- 58564r(r+2) | (1+r)²( 58564- Sr) | 58564 | S(1+r)³- 58564(r²+3r+3) |
| 4 | S(1+r)³- 58564(r²+3r+3) | Sr(1+r)³- 58564r (r²+3r+3) | (1+r)³( 58564- Sr) | 58564 | 0 |
| Итого | ________ |
| 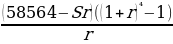
| 234256 | ________ |
Составим систему уравнений по данным таблиц:
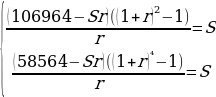
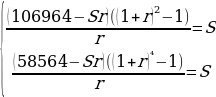 Произведем замену
Произведем замену 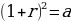
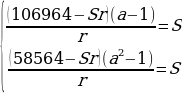
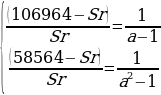
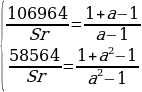
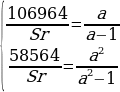

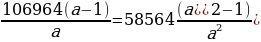
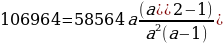
106964a=58564a+58564
48400a=58564
a=1,21
Обратная замена 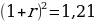 r=0,1
r=0,1
Ответ: 10% годовых.
Задачи с индивидуальным графиком погашения кредита
Существует три типа задач с индивидуальным графиком погашения кредита:
– нахождение общей суммы выплат;
– нахождение процента по кредиту;
– нахождение суммы кредита.
Задача 1. Нахождение процента по кредиту.
15-го января планируется взять кредит в банке на шесть месяцев
в размере 1 млн рублей. Условия его возврата таковы:
— 1-го числа каждого месяца долг увеличивается на r процентов
по сравнению с концом предыдущего месяца, где r — целое число;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в млн рублей) | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
Решение:
Заполним таблицу по данным задачи
| Период | Сумма долга на начало периода | Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 0,4S | Sr+0,4S | 0,6S |
| 2 | 0,6S | 0,6Sr | 0,2S | 0,6Sr+0,2S | 0,4S |
| 3 | 0,4S | 0,4Sr | 0,1S | 0,4Sr+0,1S | 0,3S |
| 4 | 0,3S | 0,3Sr | 0,1S | 0,3Sr+0,1S | 0,2S |
| 5 | 0,2S | 0,2Sr | 0,1S | 0,2Sr+0,1S | 0,1S |
| 6 | 0,1S | 0,1Sr | 0,1S | 0,1Sr+0,1S | 0 |
| Итого | ________ | 2,6Sr | S | 2,6Sr+S | ________ |
Составим неравенство по данным таблицы:
2,6Sr+S˂1,2
S(2,6r+1) ˂1,2
1(2,6r+1) ˂1,2
2,6r˂0,2
r˂ 0,076…
Ответ: 7% годовых.
Задача 16. Нахождение суммы кредита.
В июле 2016 года планируется взять кредит в банке на четыре года
в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 | Июль 2020 |
| Долг(в млн рублей) | S | 0,7S | 0,4S | 0,2S | 0 |
Найдите наименьшее значение S, при котором общая сумма выплат будет больше 10 млн рублей.
Решение:
Заполним таблицу по данным задачи
| Период | Сумма долга на начало периода | Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-4 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | Sr | 0,3S | Sr+0,3S | 0,7S |
| 2 | 0,7S | 0,7Sr | 0,3S | 0,7Sr+0,3S | 0,4S |
| 3 | 0,4S | 0,4Sr | 0,2S | 0,4Sr+0,2S | 0,2S |
| 4 | 0,2S | 0,2Sr | 0,2S | 0,2Sr+0,2S | 0 |
| Итого | ________ | 2,3Sr | S | 2,3Sr+S | ________ |
Составим неравенство по данным таблицы:
2,3Sr+S˃10
S (2,3*0,2+1) ˃10
S*1,46˃10
S˃10:1,46
S˃ 6,84…
Ответ: 7 млн. руб.
Задача 3. Нахождение общей суммы выплат.
В июле 2016 года планируется взять кредит в банке на 5 лет в размере S тысяч рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле 2017, 2018 и 2019 годов долг остается неизменно равным S тысяч рублей;
- выплаты в 2020 и 2021 годах равны по 360 тыс рублей;
- к июлю 2021 года долг будет выплачен полностью.
Найдите общую сумму выплат за 5 лет.
Решение:
Заполним таблицу по данным задачи
| Период | Сумма долга на начало периода | Сумма процентов | Погашение основной суммы долга | Сумма платежа | Сумма долга на конец периода |
| 1 | 2 | 3=5-3 | 4=5-3 | 5=3+4 | 6=2-4 |
| 1 | S | 0,2 S |
| 0,2 S | S |
| 2 | S | 0,2 S |
| 0,2 S | S |
| 3 | S | 0,2 S |
| 0,2 S | S |
| 4 | S | 0,2 S | 360- 0,2 S | 360 | 1,2 S -360 |
| 5 | 1,2 S -360 | 0,24 S-72 | 432-0,24 S | 360 | 0 |
| Итого | ________ | 1,04 S-72 | S | 0,6 S+720 | ________ |
Составим уравнение по данным таблицы:
1,04 S-72 + S=0,6 S+720
1,44 S = 792
S=792:1,44
S= 550 (тыс. руб.) – сумма кредита.
0,6*550+720 = 1050 (тыс. руб.) – общая сумма выплат.
Ответ: 1050 тыс. руб.
Задачи на вклады (вложения в бизнес-проекты)
При решении задач на кредиты рекомендую заполнять следующую таблицу
| Период | Вклад на начало периода | Пополнение вклада | Проценты | Вклад на конец периода |
| 1 | 2 | 3 | 4=(2+3)r | 5=2+3+4 |
| 1 | S |
| r |
|
| n |
| х |
|
|
| ИТОГО | ______________ |
|
| ______________ |
В задачах на кредиты введены следующие переменные:
S – сумма вклада;
r – проценты, выраженные в десятичной дроби;
n – количество периодов (начисления процентов).
Задача 1. Нахождение размера первоначального вклада.
Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года,
а, кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 1 млн рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 10 млн рублей.
Решение:
Заполним таблицу по данным задачи
| Период | Вклад на начало периода | Пополнение вклада | Проценты | Вклад на конец периода |
| 1 | 2 | 3 | 4=(2+3)r | 5=2+3+4 |
| 1 | S |
| 0,1S | 1,1S |
| 2 | 1,1S |
| 0,11S |
|
| 3 | 1,21S | 1 | 0,121S+0,1 | 1,331S+1,1 |
| 4 | 1,331S+1,1 | 1 | 0,1331S+0,21 | 1,4641S+2,31 |
| ИТОГО | ______________ | 2 | 0,4641S+0,31 | ______________ |
Составим неравенство по данным таблицы:
1,4641S+2,31˃10
1,4641S˃7,69
S˃7,69:1,4641
S˃5,25…
Ответ: 6 млн. руб.
Задача 2. Нахождение суммы пополнения вклада.
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвертого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х – целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 7 млн рублей.
Решение:
Заполним таблицу по данным задачи
| Период | Вклад на начало периода | Пополнение вклада | Проценты | Вклад на конец периода |
| 1 | 2 | 3 | 4=(2+3)r | 5=2+3+4 |
| 1 | 10 |
| 1 | 11 |
| 2 | 11 |
| 1,1 | 12,1 |
| 3 | 12,1 | х | 1,21+0,1 х | 13,31+ 1,1х |
| 4 | 13,31+ 1,1х | х | 1,331 + 0,21х | 14,641 + 2,31 х |
| ИТОГО | ______________ | 2х | 4,641 + 0,31 х | ______________ |
Составим неравенство по данным таблицы:
4,641 + 0,31 х˃7
0,31 х 7 - 4,641
х 2,359 : 0,31
х 7,60…
Ответ: 8 млн. руб.







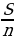
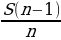
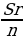
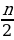 =
= 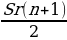
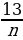 =1,56 n=10 (кредит взят на 10 лет)
=1,56 n=10 (кредит взят на 10 лет)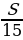
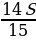
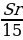
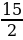 = 8Sr
= 8Sr 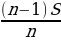
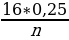 +16*0,25)
+16*0,25)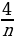 +4)
+4)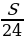
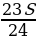
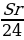
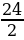 =
=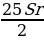
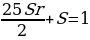 1,25S=1
1,25S=1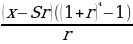
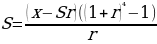
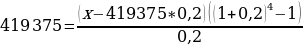
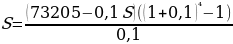
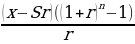
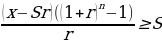
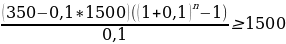
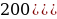
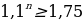 n≥
n≥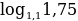 n=6 (лет)
n=6 (лет)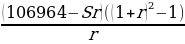
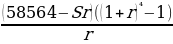
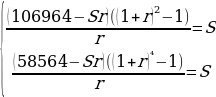
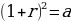
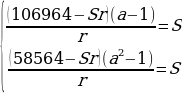
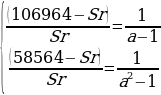
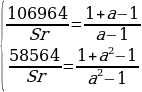
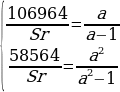

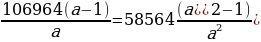
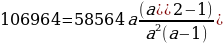
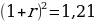 r=0,1
r=0,1


















