Конспект урока алгебры в 8 классе
Тема: «Решение систем уравнений с двумя переменными»
Цель: Обобщение и закрепление знаний и умений учащихся при решении систем уравнений различными способами.
Решать методом подстановки и сложения системы уравнений с двумя переменными, составленные из уравнения первой степени и уравнения второй степени.
Задачи:
Закрепить навыки решения систем методом подстановки, методом сложения
Развивать навыки самостоятельной работы и работы по заданному алгоритму.
Воспитывать чувство ответственности за начатое дело, чувство коллективизма, товарищества. Прививать интерес к предмету.
4.Формировать математическую грамотность.
Тип урока: обобщающее повторение, совершенствование ЗУН.
Оборудование, оформление: на столах у учащихся тетради, карточки с заданиями, листочки для самостоятельной работы, проектор, экран, ПК.
Планируемый результат:
Знать:
-способы решения систем линейных уравнений
Уметь:
применять удобный способ решения систем линейных уравнений
Методы работы:
а) методы организации учебно-познавательной деятельности: словесный, наглядный, практический, самостоятельная работа.
б) методы контроля и самоконтроля: устный опрос, фронтальный опрос, письменный контроль – самостоятельная работа.
Эпиграф урока слова советского математика, специалиста по теории вероятностей Бориса Владимировича Гнеденко: “Ничто так не содействует усвоению предмета, как действие с ним в разных ситуациях”.
Ход урока
1.Организационный момент. Мотивация.
Сегодняшний урок я хотела начать с философской загадки Вальтера: Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и краткое, самое дорогое, но и дёшево ценимое нами? (время).
Итак, у нас всего 40 минут и мне очень хотелось, чтобы это время пролетело для вас незаметно и с пользой.
Один из великих философов сказал: «Где есть желание – найдется путь!» Надеюсь, что вы сегодня на уроке с желанием будете решать задания, определяя свой рациональный путь.
- Какую тему мы с вами изучаем?
-Несколько уроков назад мы начали изучать системы уравнений второй степени.
-Когда впервые вы встретились с системами уравнений?
Впервые с системами, только линейных уравнений, мы столкнулись в 7 классе. Поэтому способы решения систем нам известны, Вы уже умеете решать системы уравнений различными способами.
Осталось только выбрать нужный способ при решении той или иной системы. В следующем году вам предстоит итоговая аттестация и хочу отметить, что системам уделяется внимание не только в более сложной во 2 части, но и в простой 1 части экзаменационной работы. На сегодняшнем уроке мы продолжим говорить о системах и способах их решения, вспомним всё, что умеем и знаем о системах уравнений с двумя переменными. Скоро эти знания вам пригодятся при решении задач с помощью систем уравнений. Эпиграф (на доске)
- Запишите число и тему урока. (слайд 1)
Проверка домашнего задания. №706(д, е), 711(б).
Осуществляется фронтально. Дома учащиеся решали системы линейных уравнений с двумя переменными различными способами. Проверка проводится устно, учащиеся называют ответ и указывают способ решения.
Повторение пройденного материала (Фронтальный опрос)
Слайд 2,3
-Успеха при решении систем уравнений без знания теории не будет. Итак,
-Какие виды уравнений с двумя переменными вы знаете? (Линейные и нелинейные)
Какое уравнение называется линейным с двумя переменными? Пример. (Уравнение вида ax + by = c, где a, b, c - некоторые числа).
Приведите пример нелинейного уравнения с двумя переменными, назовите его степень? (Н-р, x2 =4- y2 (вторая степень), 5x3+ у2 =9 (третья степень));
Что называется решением уравнения с двумя переменными? (Пара чисел (x;y), которая обращает уравнение в верное числовое равенство).
Что является графиком уравнения с двумя переменными?
Что является графиком линейного уравнения? (Прямая линия).
Что является графиком уравнения второй степени?
Что называется решением системы уравнений с двумя переменными?
(Пара чисел (х; у), которая одновременно является решением и первого, и второго уравнений системы).
Сколько решений может иметь система двух линейных уравнений с двумя переменными? (Одно, нет решений и бесконечно много решений).
Как сопоставить количество решений системы с расположением прямых в координатной плоскости? (Прямые пересекаются – одно решение; прямые параллельны – решений нет, прямые совпадают – решений много).
Как определить количество решений системы, не решая её алгебраическим способом?
(Система двух линейных уравнений с двумя переменными может быть представлена в виде:
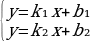
1) Если k1 ≠ k2, то прямые пересекаются и система имеет единственное решение ;
2) Если k1 = k2, но b1 ≠ b2, то прямые параллельны и система не имеет решений;
3) Если k1 = k2, но b1 = b2, то прямые совпадают и система имеет бесконечно много решений.
3.Устный счёт (Слайд 4)
- Назовите методы решения систем уравнений.
(Графический метод, метод подстановки и метод алгебраического сложения)
-В чём недостаток графического метода решения систем уравнений?
(Даёт приближённые решения данной системы)
-Сколько решений имеет система уравнений
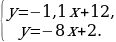

 Ответ: Одно Нет Много
Ответ: Одно Нет Много
-Укажите какое либо значение «а», при котором система имеет единственное решение; не имеет решений
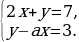
- Проходят ли через одну точку прямые:
а) 2х + у = 20 и 3х – у = 11 (да)
б) у + 3х = 5 и 3х + у = 8 (нет) ?
4. Решение систем линейных уравнений
- Давайте вспомним на практике известные вам способы решения систем уравнений с двумя переменными.
- Сейчас решим системы линейных уравнений различными способами. Я предлагаю вам в каждом случае выбрать наиболее удобный метод решения.
Задания из учебника №705(б, г), 706(в). Работаем у доски (3 ученика)
Три ученика выполняют задание, объясняя почему выбрали такой способ решения и проговаривая алгоритм решения, остальные работают на месте.
1. 
2. 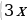 2 – 2у = 1
2 – 2у = 1
2х2 – у2 = 1
3. х2 + у2 = 5,
х + у = -3
5.Гимнастика для глаз (Слайд 5)
Смотрим в окошко на самый дальний предмет и переносим взгляд на кончик носа, потом на предмет на столе. (5-6 раз)
Закрыть глаза. Сделать 10 кругов глазами по часовой стрелке и 10 кругов против часовой. Нарисовать глазами + (вверх-вниз, вправо- влево)
4.Самостоятельная работа
- А теперь проверим, как вы усвоили материал. Выполните самостоятельно следующее задание на карточках.
После выполнения работы, дети обмениваются тетрадями, проверяют и оценивают.
| Вариант 1 1. 
2. 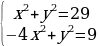
| Вариант 2 1. 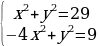 2. 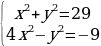 |
| Вариант 3 1. 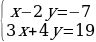 2. 2. 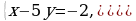 . . |
7 . Оценки за самостоятельную работу.
8. Подведение итогов, домашнее задание. Рефлексия.
— Вот и подходит к концу наш урок.
Мы рассмотрели закрепили различные способы решения системы уравнений.
Одну и туже систему можно решить различными способами. Каждый выберет для себя способ, который ему больше всего понравился, самое главное – чтобы каждый из Вас научился решать системы такого вида и поэтому эпиграфом урока могли служить слова советского математика, специалиста по теории вероятностей Бориса Владимировича Гнеденко: “Ничто так не содействует усвоению предмета, как действие с ним в разных ситуациях”.
- Спасибо вам, ребята, за урок.
Домашнее задание.
А теперь запишите домашнее задание: №709 и каждому составить кроссворд на тему «Уравнения с двумя переменными и их системы»
Приложение №1
Корточки для самостоятельной работы
| Вариант 1 1. 
2. 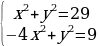
|
| Вариант 2 1. 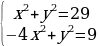 2. 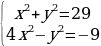 |
| Вариант 3 1. 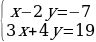 2. 2. 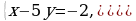 . . |
“Ничто так не
содействует усвоению предмета, как действие с ним в разных ситуациях”
Борис Владимирович Гнеденко






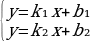
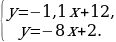

 Ответ: Одно Нет Много
Ответ: Одно Нет Много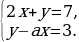

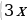 2 – 2у = 1
2 – 2у = 1
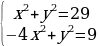
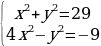
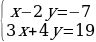 2.
2. 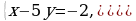 .
.









