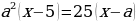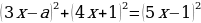Решение уравнений с параметром.
-
Линейное уравнение с параметром.
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Пример 1. 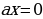
-
Если 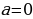 , то
, то 
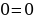
х – любое действительное число
-
Если 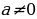 , то
, то 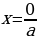
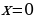
Ответ: при 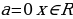 ; при
; при 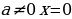
Пример 2. 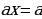
-
Если 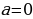 , то
, то 
х – любое действительное число
-
Если 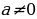 , то
, то 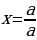
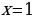
Ответ: при 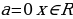 ; при
; при 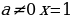
Пример 3. 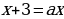
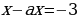
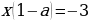
-
Если 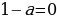 т.е.
т.е. 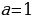 , то
, то 

уравнение корней не имеет
-
Если 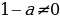 , т.е.
, т.е. 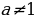 , то
, то 
Ответ: при 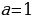 корней нет; при
корней нет; при 
Пример 4. 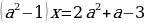
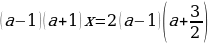
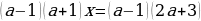
-
Если 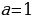 , то
, то 
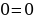
х – любое действительное число
-
Если 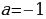 , то
, то 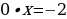
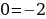
Корней нет
-
Если  , то
, то  (единственное решение).
(единственное решение).
Это значит, что каждому допустимому значению а соответствует единственное значение х.
Ответ: при 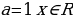 ; при
; при 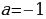 корней нет; при
корней нет; при 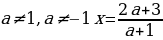
Примеры для самостоятельной работы:
Решить уравнение с параметром:
-
Квадратное уравнение с параметром.
Пример 1. 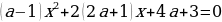
-
Если 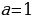 , то
, то 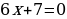

-
Если 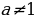 , то решим квадратное уравнение с помощью дискриминанта.
, то решим квадратное уравнение с помощью дискриминанта.

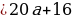
Если  , то
, то  и уравнение не имеет действительных корней.
и уравнение не имеет действительных корней.
Если  , то
, то  и уравнение имеет единственный корень:
и уравнение имеет единственный корень: 
Если  , то
, то  и уравнение имеет два корня:
и уравнение имеет два корня:
Ответ: при 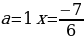 ; при
; при 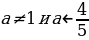 корней нет,
корней нет, 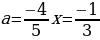 ,
,
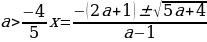
Пример 2. При каких значениях параметра а уравнение 
имеет 2 различных отрицательных корня?
-
Если 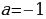 , то
, то 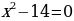
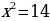

Т.е. уравнение имеет 2 корня: положительный и отрицательный, что противоречит заданию.
-
Если 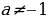 , то уравнение имеет два корня, при
, то уравнение имеет два корня, при  . Находим дискриминант.
. Находим дискриминант.
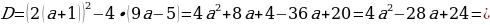

Так как  , то
, то 
В этом случае уравнение имеет 2 два корня. Воспользуемся теоремой Виета.
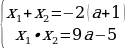
Так как по условию задачи 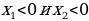 , то
, то 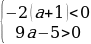
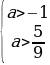
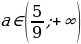
В результате: 
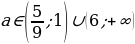
Значит, уравнение имеет два различных отрицательных корня при
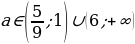
Ответ: 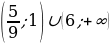
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
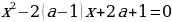
-
Если 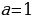 , то
, то  и уравнение корней не имеет.
и уравнение корней не имеет.
-
Если 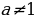 , то уравнение имеет корни при
, то уравнение имеет корни при 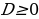 .
.
Находим дискриминант: 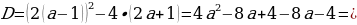
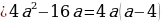
Так как 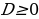 , то
, то 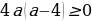
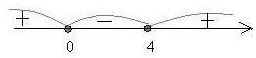
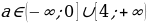
Ответ: 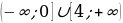
Вопросы для закрепления:
-
При каком значении а уравнение 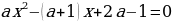 имеет один корень?
имеет один корень?
-
При каком значении а уравнение 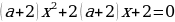 имеет один корень?
имеет один корень?
-
При каких значениях а уравнение 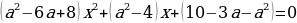 имеет более двух корней?
имеет более двух корней?
-
При каких значениях а уравнение 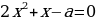 имеет хотя бы один общий корень с уравнением
имеет хотя бы один общий корень с уравнением 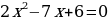 ?
?
-
При каких значениях а уравнения 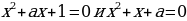 имеют хотя бы один общий корень?
имеют хотя бы один общий корень?
-
При каких значениях k произведение корней квадратного уравнения
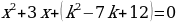 равно 0?
равно 0?
-
При каких значениях k сумма корней квадратного уравнения:
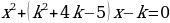 равна 0?
равна 0?
-
В уравнении 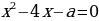 сумма квадратов корней равна 16. Найдите а.
сумма квадратов корней равна 16. Найдите а.
-
При каком значении параметра т сумма квадратов корней уравнения
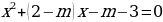 наименьшая?
наименьшая?
-
При каком значении параметра т сумма квадратов корней уравнения
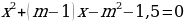 наибольшая?
наибольшая?
-
Найдите сумму квадратов всех корней уравнения 
-
При каких значениях р и q корни уравнения  равны
равны 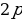 и
и 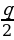 ?
?
-
При каких значениях параметра а один из корней квадратного уравнения
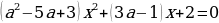 в два раза больше другого?
в два раза больше другого?
-
Известно, что корни уравнения 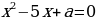 на 1 меньше корней уравнения
на 1 меньше корней уравнения
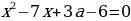 . Найдите а и корни каждого уравнения.
. Найдите а и корни каждого уравнения.
-
Известно, что корни уравнения 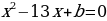 равны соответственно квадратам корней уравнения
равны соответственно квадратам корней уравнения 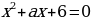 . Найти a, b и корни каждого уравнения.
. Найти a, b и корни каждого уравнения.
-
При каких значениях параметра с уравнение 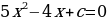 :
:
-
имеет различные действительные корни;
-
имеет один корень;
-
не имеет действительных корней;
-
имеет хотя бы один общий корень с уравнением 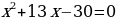 .
.
-
При каких значениях параметра b уравнение 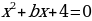 :
:
-
имеет один из корней, равный 3;
-
имеет различные действительные корни;
-
имеет один корень;
-
не имеет действительных корней.
-
При каких значениях параметра b корни уравнения 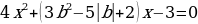 равны по модулю?
равны по модулю?
-
Найдите наибольшее целое значение k, при котором уравнение  не имеет действительных корней.
не имеет действительных корней.
-
Найдите наименьшее целое значение а, при котором уравнение
 имеет два различных действительных корня.
имеет два различных действительных корня.
-
При каком значении а уравнение 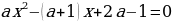 имеет один корень?
имеет один корень?
-
При каком значении а уравнение 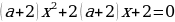 имеет один корень
имеет один корень
-
При каких значениях а уравнение 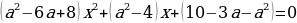 имеет более двух корней?
имеет более двух корней?
-
При каких значениях а уравнения 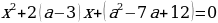 и
и
 равносильны?
равносильны?
-
Докажите, что корни уравнения  , где p и q – нечётные числа, иррациональны.
, где p и q – нечётные числа, иррациональны.
Примеры для самостоятельной работы
-
Решить уравнения с параметром:
=0 имеет два различных действительных корня.
)=0 имеет более двух корней?
3







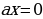
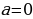 , то
, то 
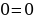
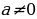 , то
, то 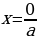
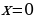
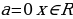 ; при
; при 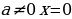
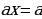
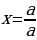
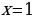
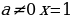
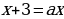
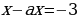
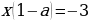
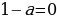 т.е.
т.е. 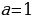 , то
, то 

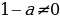 , т.е.
, т.е. 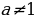 , то
, то 

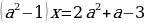
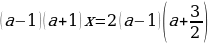
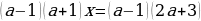
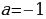 , то
, то 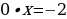
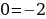
 , то
, то  (единственное решение).
(единственное решение).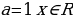 ; при
; при 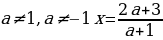
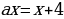
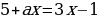

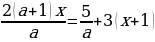
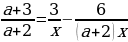
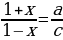
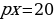
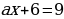
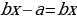
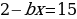


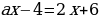
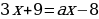
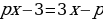
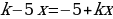
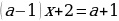
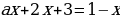
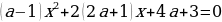
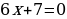


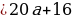
 , то
, то  и уравнение не имеет действительных корней.
и уравнение не имеет действительных корней. , то
, то  и уравнение имеет единственный корень:
и уравнение имеет единственный корень: 
 , то
, то  и уравнение имеет два корня:
и уравнение имеет два корня:
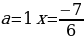 ; при
; при 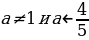 корней нет,
корней нет, 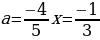 ,
,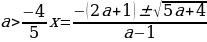

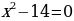
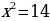

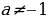 , то уравнение имеет два корня, при
, то уравнение имеет два корня, при 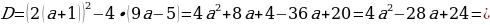


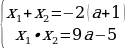
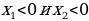 , то
, то 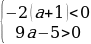
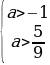
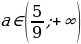

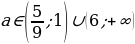
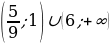
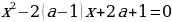
 и уравнение корней не имеет.
и уравнение корней не имеет.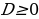 .
.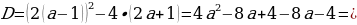
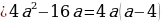
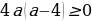

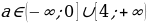
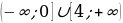
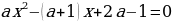 имеет один корень?
имеет один корень?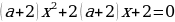 имеет один корень?
имеет один корень?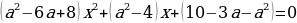 имеет более двух корней?
имеет более двух корней?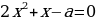 имеет хотя бы один общий корень с уравнением
имеет хотя бы один общий корень с уравнением 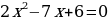 ?
?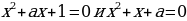 имеют хотя бы один общий корень?
имеют хотя бы один общий корень?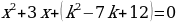 равно 0?
равно 0?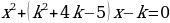 равна 0?
равна 0?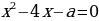 сумма квадратов корней равна 16. Найдите а.
сумма квадратов корней равна 16. Найдите а.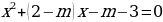 наименьшая?
наименьшая?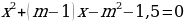 наибольшая?
наибольшая?
 равны
равны 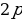 и
и 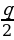 ?
?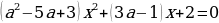 в два раза больше другого?
в два раза больше другого?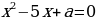 на 1 меньше корней уравнения
на 1 меньше корней уравнения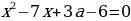 . Найдите а и корни каждого уравнения.
. Найдите а и корни каждого уравнения.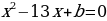 равны соответственно квадратам корней уравнения
равны соответственно квадратам корней уравнения 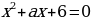 . Найти a, b и корни каждого уравнения.
. Найти a, b и корни каждого уравнения.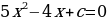 :
: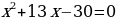 .
.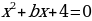 :
: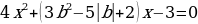 равны по модулю?
равны по модулю? не имеет действительных корней.
не имеет действительных корней. имеет два различных действительных корня.
имеет два различных действительных корня.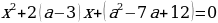 и
и  равносильны?
равносильны?