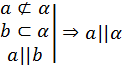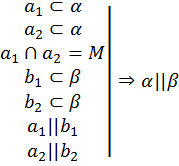Раздел. Прямые и плоскости в пространстве
Практическое занятие.
Тема: Решение задач на признаки взаимного расположения прямых в пространстве, расположения прямых и плоскостей
Цель: обобщить теоретические знания по данной теме
Оборудование: тетрадь, ручка, карандаш, линейка методические рекомендации по выполнению работы
Указания: Практическая работа состоит из двух частей теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.
1. Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
2. Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы:
Три аксиомы, выражающие основные свойства плоскостей в пространстве.
Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2. Если две точки прямой принадлежат плоскости, то и вся прямая лежит в этой плоскости.
Аксиома 3. Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (т.е. плоскости имеют общую прямую, на которой лежат все общие точки этих плоскостей).
Следствием этих аксиом являются следующие теоремы (доказательства этих теорем и всех последующих опускаем):
Теорема 1. Через прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.
Теорема 2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
Теорема 3. Через две параллельные прямые можно провести единственную плоскость.
Взаимное расположение прямых.
Возможны три случая: две прямые параллельны, пересекаются или скрещиваются.
| Определение. Две прямые называются пересекающимися, если они имеют одну общую точку. Обозначение: a ∩ b = M | α a b  M |
| Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. Обозначение: a || b | a   α b |
| Определение. Две прямые, не лежащие в одной плоскости, называются скрещивающимися. Обозначение: a ∸ b | a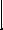 b M α  |
| Теорема 4 (признак скрещивающихся прямых): Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются. | 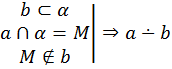
|
| Пример: Две прямые, содержащие ребра AA1 и CD куба ABCDA1B1C1D1 являются скрещивающимися. | С 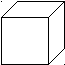 1 1 В1 D 1 1 А1 В С D   А |
Взаимное расположение прямой и плоскости.
Возможны три случая: прямая лежит в плоскости; прямая пересекает плоскость; прямая и плоскость параллельны.
| Определение. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в плоскости. Обозначение: a α | a α 
|
| Определение. Прямая и плоскость называются пересекающимися, если у них есть одна общая точка. Обозначение: a ∩ β = M | a β  
|
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Обозначение: a || a ∩ β =
| Теорема 5 (признак параллельности прямой и плоскости): Если прямая, не лежащая в плоскости, параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна данной плоскости. 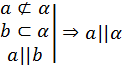
| a   b α |
Взаимное расположение плоскостей.
Возможны два случая: две плоскости пересекаются или параллельны.
Определение. Две плоскости называются параллельными, если они не имеют общих точек
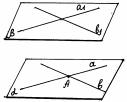
| Теорема 6 (признак параллельности плоскостей): Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны. 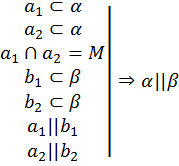
| a1 a 2 2 α  M b   1 1 b2 β |
| Определение. Две плоскости называются пересекающимися, если они имеют общую прямую. В этом случае они не имеют других общих точек вне этой прямой. α ∩ β = a | β 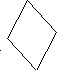         α a |
Задания на закрепление:
1. Дан куб ABCDA1B1C1D1. Точка М – середина ребра B1C1, N – середина C1D1, K – середина DC, О – точка пересечения диагоналей основания ABCD. Укажите взаимное расположение между следующими прямыми:
а) АA1 и CС1; б) A1C1 и B1D1; в) A1C1 и C1D1;
г) A1М и CC1; д) A1D и DC1; е) A1C1 и BD;
ё) A1C и АС; ж) A1B и D1С; з) A1C и ВB1;
и) A1D и АВ; й) A1М и ВС; к) A1М и ВК ;
л) C1К и B1N; м) C1О и AB1; н) A1О и B1D.
2. Дан тетраэдр ABCD. Точка К – середина ребра AD, L – середина DB, М – середина АС, N – середина ВС. Определите взаимное расположение прямых и плоскостей.
а) DB и AMN; б) MN и ABC; в) КС и DMN;
г) MN и ABD; д) KL и DMN; е) LN и KML;
ё) CL и ADN; ж) LN и DMK.
3. Дан куб ABCDA1B1C1D1. Точка К – середина ребра AD, L – середина СC1, М – середина A1B1, N – середина B1C1, Т – середина DC, О – точка пересечения диагоналей четырёхугольника ABCD. Укажите взаимное расположение плоскостей:
а) A1B1C1 и ADC; б) MTK и BB1D; в) MNK и MNT;
г) D1KT и BMN; д) MNK и TLN; е) B1КТ и DMN;
ё) A1DC1 и АB1C; ж) A1C1С и MKT.
3. Отметьте верные утверждения
а) через точку, не принадлежащую данной прямой, можно провести только одну прямую, параллельную этой прямой.
б) через точку, не принадлежащую данной прямой, можно провести только одну прямую, перпендикулярную этой прямой.
в) прямые, перпендикулярные одной и той же прямой, параллельны.
г) прямая, пересекающая одну из двух данных параллельных прямых, пересекает и другую.
4. Даны две параллельные прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.
5. Даны две скрещивающиеся прямые а и b. Как может быть расположена по отношению к ним третья прямая c? Сделайте рисунки.
6. Отметьте верные утверждения:
а) прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.
б) существует единственная прямая, параллельная данной плоскости и проходящая через точку, не принадлежащую этой плоскости.
в) существует бесконечное множество прямых, параллельных данной плоскости и проходящих через точку, не принадлежащую этой плоскости.
г) через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.
д) существует единственная плоскость, параллельная данной прямой и проходящая через точку, не принадлежащую этой прямой.
е) существует бесконечное множество плоскостей, параллельных данной прямой и проходящих через точку, не принадлежащую этой прямой.
7. Прямые а и b скрещиваются. Можно ли провести через одну из них плоскость, параллельную другой? Обоснуйте свой ответ.
8. Отметьте верные утверждения
а) через точку, не принадлежащую данной плоскости, проходит единственная плоскость, параллельная данной.
б) если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.
в) если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.
г) если одна из двух данных плоскостей параллельна двум пересекающимся прямым, лежащим в другой плоскости, то эти плоскости параллельны.
д) если плоскость пересекает две данные плоскости по параллельным прямым, то эти плоскости параллельны.
е) если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
ж) если две плоскости параллельны одной и той же прямой, то они параллельны.
9. Точка B не лежит в плоскости треугольника ADC, точки M, N и Р середины отрезков ВА, BC и BD соответственно. Докажите, что плоскости MNP и ADC параллельны. Найдите площадь треугольника MNP, если площадь треугольника ADC равна 48 cм2.
10. Докажите, что α и β параллельны, если две пересекающиеся прямые m и n плоскости α параллельны плоскости β.
11. Плоскости α и β параллельны, А точка плоскости α. Докажите, что любая прямая, проходящая через точку A и параллельная плоскости β, лежит в плоскости α.
12. Даны пересекающиеся прямые a и b и точка A, не лежащая в плоскости этих прямых. Докажите, что через точку A проходит плоскость, параллельная прямым а и b, и притом только одна.
13. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторона параллельна плоскости α.







 1
1