Решение задач на смеси и сплавы

Решение задач на смеси и сплавы

Основная цель :

Научиться решать задачи на смеси табличным способом.

Распределение задач на проценты по классам

УМК под ред. А.Г. Мордкович

Задачи на %

Алгебра 7кл.

Задачи на растворы

Алгебра 8кл.

№ 12.23-12.25; 14.19-14.22;

Задачи на сплавы

№ 25.34; 25.35; 25.44

14.29; 14.33

нет

Алгебра 9кл.

№ 14.34 ; 14.35

№ 53 (с.11);

нет

№ 27.44; 27.45

№ 7,8,11(с.194)

№ 7.53; 7.54;

№ 12-14,16 (с.195)

№ 7.55;

№ 9, 15 (с.195)

При решении задач на проценты необходимо уметь находить процент от числа, число по его процентам, процентное отношение:

• Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту дробь.

• Чтобы найти число по данным его процентам, нужно выразить проценты в виде дроби. А затем значение процентов разделить на эту дробь.

• Чтобы найти процентное отношение двух чисел, надо отношение этих чисел умножить на 100%.

Решение задач на смеси основано на следующей формуле:

где - процентное содержание вещества в смеси,

или

Для решения задач удобно использовать таблицу

Смесь

Масса смеси, кг

Концентрация вещества, %

Масса вещества, кг

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ

• Внимательно прочитать текст задачи.
• Составить таблицу, заполняя ячейки данными из условия задачи.
• Ввести переменные, заполнить пустые ячейки выражениями, содержащими переменные.
• Составить уравнение по правилу : при объединении двух смесей их массы складываются. Аналогично, складываются и массы веществ, составляющих смеси.
• Решить уравнение.
• Выбрать ответ.

Задачи на нахождение массы исходных растворов и их концентраций

• Задача 1. В сосуд, содержащий 5 литров 12%-ого водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Раствор

Объём раствора, л

Исходный

5

Концентрация вещества, %

Вода

Новый раствор

7

12

Объём растворённого вещества, л

5+7=12

-

-

x

Ответ: 5% концентрация нового раствора .

• Задача 2. Смешали 4 литра 15%-ого водного раствора некоторого вещества с 6 литрами 25%-ого водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Раствор

Объём раствора, л

1

4

Концентрация вещества, %

2

Объём растворённого вещества, л

15

6

Новый раствор

4 + 6 = 10

25

х

Ответ: 21% составляет концентрация нового раствора.

• Задача 3. У ювелира два одинаковых по массе слитка, в одном из которых 36% золота, а в другом 64%. Сколько процентов золота содержится в сплаве, полученном из этих слитков?

Сплав

Масса сплава, г

1

m

Концентрация вещества (золота), %

2

Новый сплав

36

m

Масса вещества (золота), г

m + m = 2m

0,36m

64

0,64m

х

Ответ: 50% содержится золота в новом сплаве.

• Задача 4. Смешали 30% раствор соляной кислоты с 10%-ым и получили 600г 15%-ого раствора. Сколько граммов каждого раствора было взято?

Раствор

1

Масса раствора, г

x

Концентрация вещества, %

2

Масса растворённого вещества, г

30

600 - x

Новый раствор

600

0,3x

10

0,1(600 – x)

15

150г масса первого раствора;

600-150=450г масса второго раствора.

Ответ: 150г, 450г.

• Задача 5. Смешав 70%-й и 60%-й растворы кислоты и добавив 2кг чистой воды, получили 50%-й раствор кислоты. Если бы вместо 2кг воды добавили 2кг 90%-ого раствора той же кислоты, то получили бы 70%-ый раствор кислоты. Сколько кг 70%-ого раствора использовали для получения смеси?

Раствор

Масса раствора, г

1

x

Концентрация вещества, %

2

Масса растворённого вещества, г

Вода

y

70

2

0,7x

60

Новый раствор 1

0,6y

x + y +2

-

-

50

Раствор

Масса раствора, г

1

Концентрация вещества, %

x

2

Масса растворённого вещества, г

70

y

3

0,7x

60

2

Новый раствор 2

x + y + 2

90

0,6y

70

4кг масса 60%-ого раствора;

3кг масса 70%-ого раствора.

Ответ: 3кг.

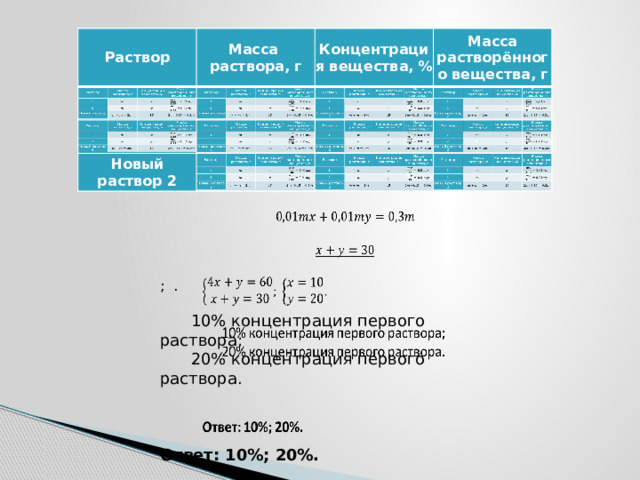
• Задача 6. Если смешать 8кг и 2кг растворов серной кислоты разной концентрации, то получим 12% раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15% раствор. Определите первоначальную концентрацию каждого раствора.

Раствор

Раствор

Масса раствора, кг

Масса раствора, кг

Концентрация вещества, %

Концентрация вещества, %

Новый раствор 1

Масса растворённого вещества, кг

Масса растворённого вещества, кг

Новый раствор 1

Раствор

Раствор

Масса раствора, г

Масса раствора, г

Концентрация вещества, %

Концентрация вещества, %

Масса растворённого вещества, г

Масса растворённого вещества, г

Новый раствор 2

Новый раствор 2

; .

10% концентрация первого раствора;

20% концентрация первого раствора.

Ответ: 10%; 20%.

• Задача 7. В смеси спирта и воды спирта в 4 раза меньше, чем воды. Когда к этой смеси добавили 20 литров воды, получили смесь с процентным содержанием спирта 12%. Сколько воды в смеси было первоначально?

Раствор

Объём раствора, л

Исходный (спирт : вода=1:4)

Концентрация вещества, %

Вода

Объём растворённого вещества, л

Новый раствор

6 литров спирта было в исходном растворе;

24 литра воды было в исходном растворе.

Ответ: 24л.

• Задача 8. Имеется два раствора кислоты. Первый раствор состоит из 1056г кислоты и 44г воды, а второй – из 756г кислоты и 1344г воды. Из этих растворов нужно получить 1500г нового раствора, содержание кислоты в котором 40%. Сколько граммов первого раствора нужно для этого взять?

Раствор

Масса раствора, г

кислота

Масса раствора, г

вода

1056

756

Новый раствор

Концентрация вещества, %

44

1344

Масса растворённого вещества, г

Концентрация кислоты в первом растворе:

Концентрация кислоты во втором растворе:

Ответ: 100г первого раствора нужно взять.

Задачи на сплавы

• Задача 9. Первый сплав серебра и меди содержит 70г меди, а второй сплав – 210г серебра и 90г меди. Сплавили кусок первого сплава с куском массой 75г второго сплава и получили 300г сплава, который содержит 82% серебра. Сколько граммов серебра содержалось в первом сплаве?

Сплав

Сплав

Масса сплава, г

Масса сплава, г

серебро

серебро

Масса куска сплава, г

медь

медь

Масса куска сплава, г

Новый сплав

Новый сплав

Концентрация вещества (серебра), %

Концентрация вещества (серебра), %

Масса серебра, г

Масса серебра, г

Концентрация серебра во втором сплаве:

Концентрация серебра в первом сплаве:

Масса серебра во втором сплаве: 246-52,5=193,5

Ответ: 430г серебра содержалось в первом сплаве.

• Задача 10. Латунь - сплав меди и цинка. Кусок латуни содержит цинка на 80кг меньше, чем меди. Этот кусок латуни сплавили со 120 кг меди и получили латунь, в которой 75% меди. Определите массу (в килограммах) первоначального куска латуни.

Сплав

Масса сплава, кг

Исходный

(медь+ цинк)

Медь

Концентрация меди, %

Новый сплав

Масса меди, кг

100кг масса цинка в исходном сплаве;

кг масса первоначального куска латуни

Ответ: 280кг.

• Задача 11. Отношение массы олова к массе свинца в куске сплава равно 2:3. Этот кусок сплавили с куском олова весом 3кг и получили новый сплав с процентным содержанием свинца 10%. Найдите массу олова в новом сплаве.

Сплав

Сплав

Масса сплава, кг

Масса сплава, кг

(олово +свинец)

(олово +свинец)

Исходный

Концентрация , %

Исходный

Концентрация , %

олово

Олово

Олово

олово

свинец

Новый сплав

Масса олова, кг

Новый сплав

свинец

Масса олова, кг

0,12кг масса одной части исходного сплава; кг масса олова в новом сплаве.

Ответ: 3,24кг.

• Задача 12. Сплав золота с серебром, содержащий 80г золота, сплавили со 100г чистого золота. В результате содержание золота в сплаве повысилось по сравнению с первоначальным на 20%. Сколько граммов серебра в сплаве?

Сплав

Сплав

Исходный

Масса сплава, г

Исходный

Масса сплава, г

Золото

Золото

Концентрация золота, %

Концентрация золота, %

Масса золота, г

Новый сплав

Масса золота, г

Новый сплав

200г масса исходного сплава;

г масса серебра в исходном сплаве.

Ответ: 120г.

Задачи на изменение концентрации (процессы сушки, выпаривания)

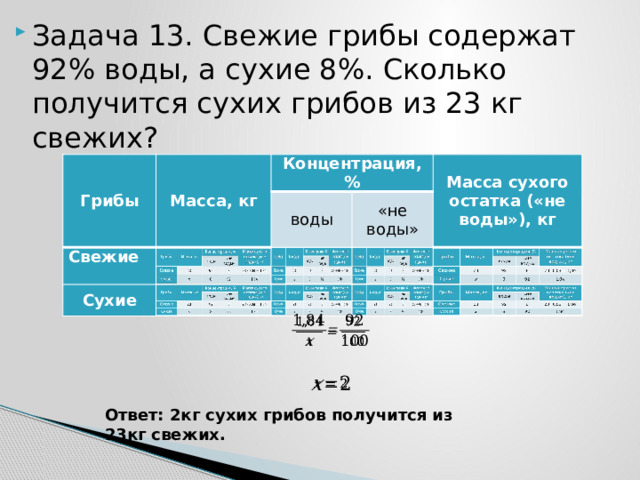
• Задача 13. Свежие грибы содержат 92% воды, а сухие 8%. Сколько получится сухих грибов из 23 кг свежих?

Грибы

Грибы

Масса, кг

Масса, кг

Свежие

Концентрация, %

Концентрация, %

Свежие

Сухие

воды

воды

Сухие

«не воды»

Масса сухого остатка («не воды»), кг

Масса сухого остатка («не воды»), кг

«не воды»

Ответ: 2кг сухих грибов получится из 23кг свежих.

• Задача 14. Сколько кг воды нужно выпарить из 2 тонн целлюлозной массы, содержащей 85% воды, чтобы получить массу с 75% содержанием воды?

Целлюлозная масса

Масса, кг

Исходная масса

Концентрация, %

Масса после выпаривания

воды

85

«не воды»

Масса сухого остатка («не воды»), кг

1200кг масса целлюлозы после выпаривания;

кг воды нужно выпарить

Ответ: 800кг.

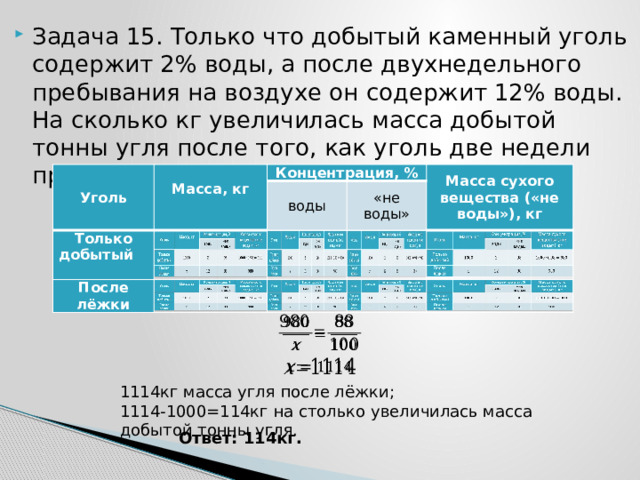
• Задача 15. Только что добытый каменный уголь содержит 2% воды, а после двухнедельного пребывания на воздухе он содержит 12% воды. На сколько кг увеличилась масса добытой тонны угля после того, как уголь две недели пролежал на воздухе?

Уголь

Масса, кг

Только добытый

Концентрация, %

После лёжки

воды

«не воды»

Масса сухого вещества («не воды»), кг

1114кг масса угля после лёжки;

1114-1000=114кг на столько увеличилась масса добытой тонны угля.

Ответ: 114кг.

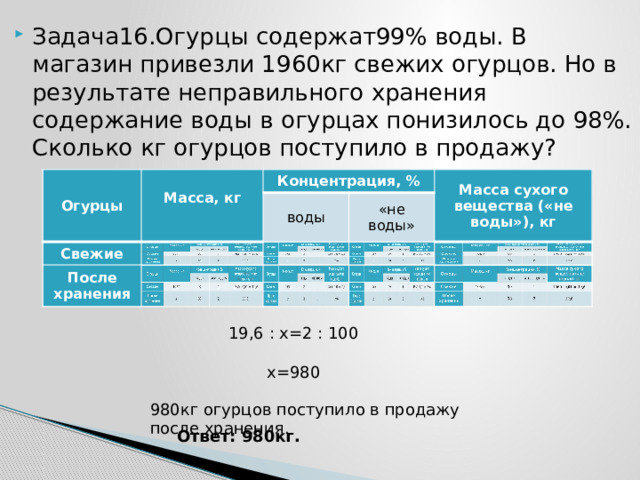
• Задача16.Огурцы содержат99% воды. В магазин привезли 1960кг свежих огурцов. Но в результате неправильного хранения содержание воды в огурцах понизилось до 98%. Сколько кг огурцов поступило в продажу?

Огурцы

Огурцы

Масса, кг

Масса, кг

Концентрация, %

Свежие

Концентрация, %

Свежие

воды

воды

После хранения

После хранения

Масса сухого вещества («не воды»), кг

«не воды»

Масса сухого вещества («не воды»), кг

«не воды»

19,6 : x=2 : 100

x=980

980кг огурцов поступило в продажу после хранения.

Ответ: 980кг.

Задачи на соотношения компонентов

• Задача17. Имеются два сплава с разным содержанием золота. В первом сплаве содержится 30%, а во втором 55% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?

Сплав

Сплав

Масса сплава, г

I

Масса сплава, г

I

II

Концентрация золота, %

Концентрация золота, %

II

Новый сплав

Масса золота, г

Масса золота, г

Новый сплав

(x + y)∙0,4 = 0,3x+0,55y

0,1x = 0,15y

x : y = 3 : 2

Ответ: Сплавы нужно взять в отношении 3:2.

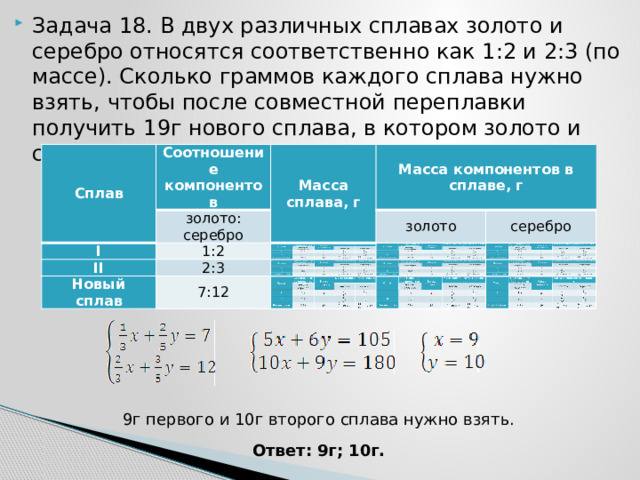
• Задача 18. В двух различных сплавах золото и серебро относятся соответственно как 1:2 и 2:3 (по массе). Сколько граммов каждого сплава нужно взять, чтобы после совместной переплавки получить 19г нового сплава, в котором золото и серебро находятся в отношении 7:12?

Сплав

Сплав

Соотношение компонентов

Соотношение компонентов

Масса сплава, г

Ι

Масса сплава, г

золото: серебро

золото: серебро

Ι

Масса компонентов в сплаве, г

Масса компонентов в сплаве, г

1:2

1:2

ΙΙ

ΙΙ

Новый сплав

2:3

Новый сплав

золото

золото

2:3

7:12

7:12

серебро

серебро

9г первого и 10г второго сплава нужно взять.

Ответ: 9г; 10г.

• Задача 19. Ювелирное изделие состоит из серебра и золота. В начале года серебро дорожает на 5%, а золото на20% по сравнению с предыдущим годом, в результате чего стоимость ювелирного изделия увеличивается на 15%. Какую часть ювелирного изделия составляет золото, если в предыдущем году 1г золота стоил в 18раз дороже 1г серебра? (Ответ записать в виде десятичной дроби)

Стоимость 1грамма

Стоимость 1грамма

серебро

серебро

Было

Было

Стало

Стоимость в изделии

золото

Стало

золото

Стоимость в изделии

серебро

серебро

Стоимость изделия

золото

Стоимость изделия

золото

Пусть в изделии отношение серебро : золото составляет x : y соответственно.

(mx+18my)∙1,15=1,05mx+21,6my

1,15x+20,7y=1,05x+21,6y

0,1x=0,9y

x : y = 9 : 1

Ювелирное изделие состоит из десяти частей сплава серебра и золота. На золото приходится одна часть.

Ответ: 0,1

• Задача 20. Имеются два слитка золота и серебра. В первом отношение золота и серебра равно 1:2. во втором 2:3. Если сплавить 1/3первоначального слитка и 5/6 второго, то в полученном слитке будет столько золота, сколько в первом было серебра.

Если же 2/3 первого слитка сплавить с половиной второго, то в полученном слитке серебра будет на 1кг больше, чем было золота во втором слитке. Сколько золота в каждом слитке?

Сплав

Соотношение компонентов

Ι

Масса сплава

золото: серебро

ΙΙ

Масса компонентов в сплаве

1:2

золото

2:3

серебро

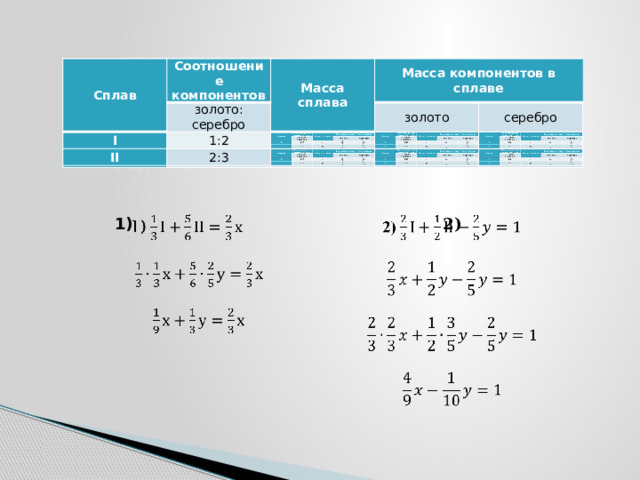
Сплав

Сплав

Соотношение компонентов

Соотношение компонентов

золото: серебро

Масса сплава

Ι

Ι

Масса сплава

золото: серебро

ΙΙ

1:2

ΙΙ

1:2

Масса компонентов в сплаве

Масса компонентов в сплаве

2:3

золото

золото

2:3

серебро

серебро

2)

1)

3,6кг масса первого слитка ; 6кг масса второго слитка .

1,2кг масса золота в первом слитке.

2,4кг масса золота во втором слитке.

Ответ: Масса золота во втором слитке больше, чем в первом.

Задачи на разбавление

• Задача 21. В колбе было 800г 80%-ого спирта. Провизор отлил из колбы 200г этого спирта и затем добавил в неё столько же воды. Определите концентрацию (в %) полученного спирта.

Раствор

Раствор

Масса раствора, г

Было

Было

Масса раствора, г

Отлил раствор

Концентрация вещества, %

Отлил раствор

Концентрация вещества, %

Добавил воду

Масса растворённого вещества, г

Масса растворённого вещества, г

Добавил воду

Новый раствор

Новый раствор

8x=640-160

8x=480

x=60

Ответ: 60% концентрация полученного спирта.

• Задача 22. Из сосуда, доверху наполненного 99% раствором кислоты, отлили 3,5литра жидкости и долили 3,5 литра 51%-ого раствора этой же кислоты. После этого в сосуде получился 89% раствор кислоты. Сколько литров раствора вмещает сосуд?

Раствор

Раствор

Объём раствора, л

Было

Было

Объём раствора, л

Концентрация вещества, %

Отлили исх. раствор

Отлили исх. раствор

Концентрация вещества, %

Добавили раствор

Объём растворённого вещества, л

Добавили раствор

Объём растворённого вещества, л

Новый раствор

Новый раствор

Ответ: 16,8л раствора вмещает сосуд.

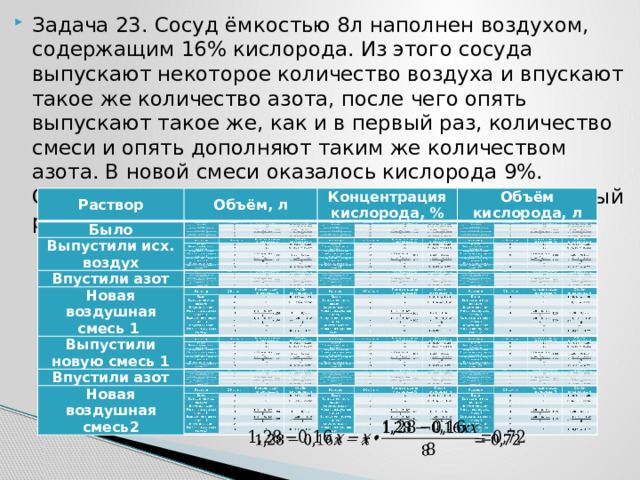
• Задача 23. Сосуд ёмкостью 8л наполнен воздухом, содержащим 16% кислорода. Из этого сосуда выпускают некоторое количество воздуха и впускают такое же количество азота, после чего опять выпускают такое же, как и в первый раз, количество смеси и опять дополняют таким же количеством азота. В новой смеси оказалось кислорода 9%. Определите, по скольку литров выпускалось каждый раз из сосуда.

Раствор

Раствор

Объём, л

Было

Было

Объём, л

Концентрация кислорода, %

Выпустили исх. воздух

Концентрация кислорода, %

Выпустили исх. воздух

Объём кислорода, л

Объём кислорода, л

Впустили азот

Впустили азот

Новая воздушная смесь 1

Новая воздушная смесь 1

Выпустили новую смесь 1

Выпустили новую смесь 1

Впустили азот

Впустили азот

Новая воздушная смесь2

Новая воздушная смесь2

- не удовлетворяет условию задачи;

2л воздушной смеси выпускалось каждый раз.

Ответ: 2л.

• Задача 24. Из бака, наполненного спиртом, вылили часть спирта и долили водой, потом из бака вылили столько же литров смеси. После этого в баке осталось 49 литров чистого спирта. Сколько литров спирта вылили в первый раз и сколько во второй, если вместимость бака 64 литра?

Раствор

Раствор

Было

Объём раствора, л

Было

Объём раствора, л

Отлили спирт

Концентрация вещества, %

Отлили спирт

Концентрация вещества, %

Добавили воду

Объём спирта, л

Добавили воду

Объём спирта, л

Новый раствор 1

Новый раствор 1

Вылили новый раствор 1

Вылили новый раствор 1

Новый раствор 2

Новый раствор 2

– не удовлетворяет условию задачи;

8л спирта вылили первый раз;

7л спирта вылили второй раз.

Ответ:8л; 7л.

Спасибо за внимание!