Решение задач на смеси и сплавы

Тема урока: Решение задач на смеси, растворы, сплавы.

9класс (алгебра)

Верю – не верю

1)

2) Концентрация раствора 3% означает, что в 100 г раствора 30 г вещества.

3) = 30 %

4) Золотое кольцо имеет пробу 583. Это означает, что

на 1 кг сплава содержится 583 грамма чистого золота.

5) 75% = 0,75

Цель урока?

Ч тобы лучше понимать условия задач, необходимо знать следующие понятия:

• Все получающиеся сплавы или смеси однородны.
• При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
• Процент - одна сотая любого вещества.  
• Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.  
• Это отношение может быть выражено либо в дробях, либо в процентах.
• Сумма концентраций всех компонент, составляющих смесь, равна единице.

Задача 1 . Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение: 1 способ – с помощью таблицы:

Наименование веществ, смесей

Наименование веществ, смесей

Исходный раствор

70 % = 0,7

Масса

Воды долили

Новый раствор

-

200

Масса вещества (г)

раствора (г)

8 % = 0,08

0,7·200

x

200 + x

-

0,08(200 + x)

Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение :

0,08(200 + х) = 0,7·200

16 + 0,08х = 140

0,08х = 124

х = 1550

Ответ :1,55 кг воды.

2 способ - с помощью схемы: Пусть в сосуд долили х литров воды. Получаем схему:

Уксусная Уксусная

кислота кислота

70% + х литров 8%

воды

200 г. (200 + х) г.

0,08(200 + х) = 0,7·200

16 + 0,08х = 140

0,08х = 124

х = 1550

Ответ :1,55 кг воды.

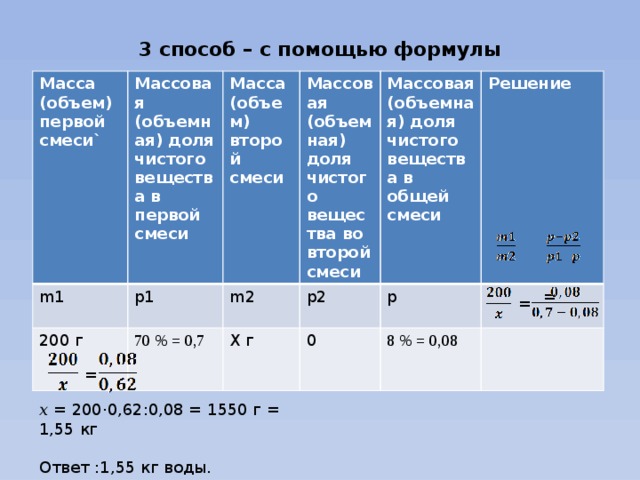
3 способ – с помощью формулы

Масса (объем) первой смеси`

Массовая (объемная) доля чистого вещества в первой смеси

m1

p1

Масса (объем) второй смеси

200 г

m2

70 % = 0,7

Массовая (объемная) доля чистого вещества во второй смеси

Х г

p2

Массовая (объемная) доля чистого вещества в общей смеси

Решение

0

p

8 % = 0,08

=

=

=

𝑥 = 200·0,62:0,08 = 1550 г = 1,55 кг

Ответ :1,55 кг воды.

Задача 2: Смешали некоторое количество 15 % раствора некоторого вещества с таким же количеством 19% раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Ответ: 17%.

Задача 3: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. На сколько граммов масса первого раствора меньше массы второго?

Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора

Самостоятельная работа

Задача : Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Ответ: 9 кг.

Домашнее задание

Учебник алгебра 9 класс А.Г. Мордкович

• 1 уровень: № 12,13 стр. 195
• 2 уровень : № 13,14 стр. 195

Заключение.

Притча

1.Кто сегодня на уроке работал как первый

каменщик?

2. Кто сегодня на уроке работал как второй

каменщик?

3. Кто принимал участие в строительстве

собственного храма знаний сегодня?

• Узнали ли для себя что-нибудь нового и полезного? Что, на ваш взгляд, мешало вам в работе? Что помогло преодолеть эти трудности? Достигли ли поставленной цели. А почему, как думаете? Каковы результаты?
• Узнали ли для себя что-нибудь нового и полезного?
• Что, на ваш взгляд, мешало вам в работе?
• Что помогло преодолеть эти трудности?
• Достигли ли поставленной цели. А почему, как думаете? Каковы результаты?

Спасибо за урок!