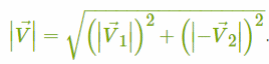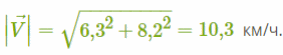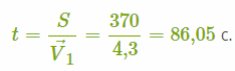Решение задач на тему: "Относительность движения и сложение скоростей".

Решение задач на тему:

Относительное движение и сложение скоростей

1. Относительное движение в одном направлении

По шоссе движется перевозчик со скоростью 13 м/с. В том же направлении движется другой перевозчик со значением скорости, равным 12,2 м/с. В ответе запиши , с какой скоростью по модулю движется первый перевозчик относительно другого.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

∣V⃗₁∣=13 м/с;

∣V⃗₂∣=12,2 м/с;

∣V⃗∣−?

Чтобы найти, с какой скоростью по модулю первый перевозчик движется относительно другого, необходимо заметить, что они оба движутся в одном направлении.

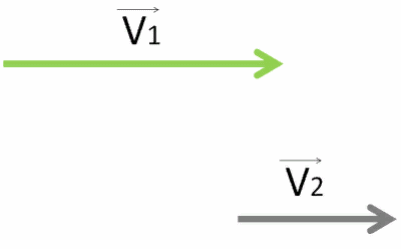
Найти скорость, с которой первый перевозчик движется относительно другого, очень просто.

Нужно отнять от его вектора скорости V⃗₁ вектор V⃗₂ , с которой движется другой перевозчик.

Чтобы это сделать, нужно к вектору V⃗₁ прибавить вектор V⃗₂, только поменяв его направление.

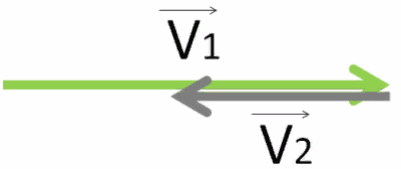
Результирующий вектор V⃗ получим, соединив начало первого вектора с концом последнего.

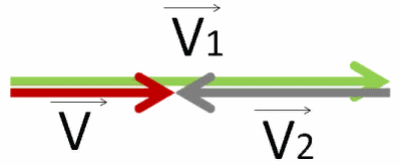
Получим вектор V⃗ красного цвета.

Чтобы найти его числовое значение, нужно от числового значения вектора V⃗₁ отнять числовое значение вектора V⃗₂ и результат взять по модулю.

Получим:

|V|=|13−12,2| = 0,8 м/с.

2. Относительная скорость тел, движущихся под прямым углом друг к другу

По свежеположенной дороге перемещается гусеничный трактор , имея скорость 6,3 км/ч. Перпендикулярно движется другой гусеничный трактор со скоростью 8,2 км/ч. Найди значение модуля скорости, с которой движется первый гусеничный трактор относительно другого.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

∣V⃗₁∣=6,3 км/ч;

∣V⃗₂∣=8,2 км/ч;

∣V⃗ ∣−?

Как мы видим, первый гусеничный трактор движется под углом 90 градусов к другому.

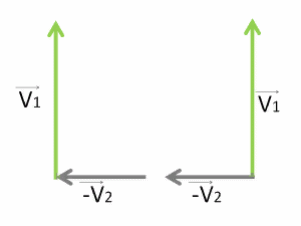
Покажем направления их скоростей с помощью векторов V⃗₁ и V⃗₂.

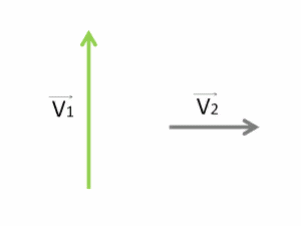
Чтобы найти скорость, с которой движется первый гусеничный трактор относительно другого, необходимо векторно от скорости первого V⃗₁ отнять скорость второго V⃗₂.

Отнимание вектора V⃗₂ проще заменить сложением вектора, противоположного ему: −V⃗₂.

Получим:

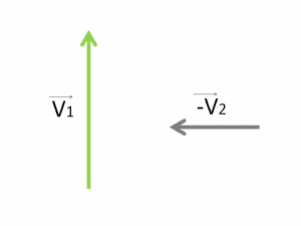
Чтобы найти результирующую скорость V⃗ , необходимо векторно сложить векторы V⃗₁ и −V⃗₂ . Для интереса попробуем это сделать двумя способами.

Выстраиваем их друг за другом, чтобы получились стороны треугольника.

Или соединяем начала этих векторов — тогда будем использовать правило параллелограмма.

Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Должен получиться один и тот же вектор V⃗ . Изобразим его красным.

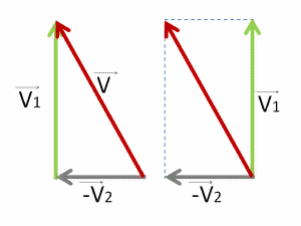
Результат сложения не зависит от выбора правила сложения — по правилу треугольника или параллелограмма.

Как видно, у нас получился прямоугольный треугольник со сторонами V⃗₁ , −V⃗₂ , V⃗ .

По условию задачи нам известны две его стороны, это два катета:

∣V⃗₁∣=6,3 км/ч и ∣−V⃗₂∣=8,2 км/ч.

Используя теорему Пифагора, мы можем найти гипотенузу V⃗:

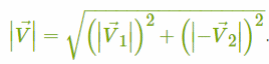
Численно получим:

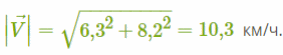
3. Относительная скорость течения реки

Величина скорости пловца вверх по течению реки относительно припаркованного возле магазина мотоцикла — 28,5 км/ч, а вниз по реке — 32,9 км/ч.

Напиши , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

V_po=32,9 км/ч;

V_pro=28,5 км/ч;

V⃗₂−?

Попробуем представить себе, как движется пловец по течению. Если обозначить эту скорость V⃗₁, а течение реки V⃗₂, то, скорее всего, это будет выглядеть так:

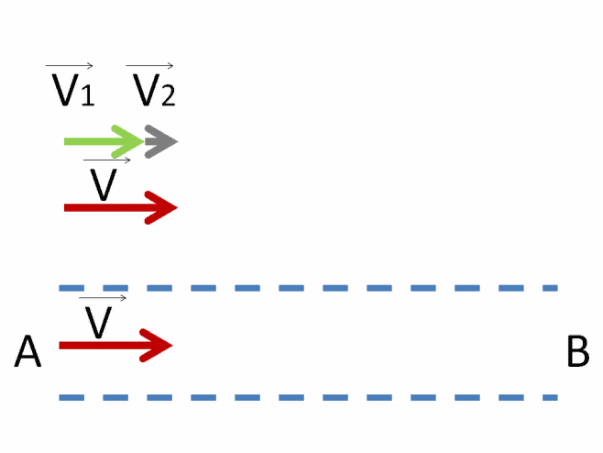
Как видно, результирующий вектор V⃗ получился равным сумме векторов V⃗₁ и V⃗₂ .

Именно с такой скоростью движется пловец по течению.

Если показывать движение пловца против течения, то с теми же обозначениями получим:

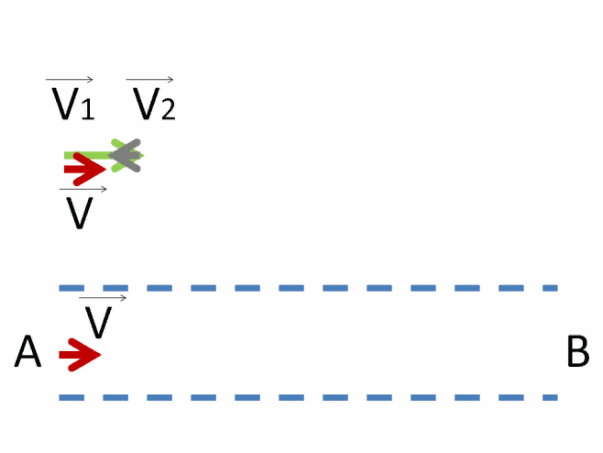
Как видно, уже в этом случае результирующий вектор скорости пловца V⃗ стал меньше, т.к. он равен разности векторов V⃗ 1 и V⃗ 2 . Оно и понятно, ведь против течения двигаться сложнее, скорость пловца меньше из-за встречного течения воды.

Это хорошо, что мы представили себе эту задачу. Но чтобы её решить, нужно составить уравнения движения по течению и против течения реки:

V₁+V₂=32,9;

V₁−V₂=28,5.

В математике это называется системой уравнений.

Не забывай, что найти нам нужно , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла, т.е. V⃗₂.

Попробуем выразить её из первого уравнения. Для этого V⃗₁ перенесётся в правую сторону и поменяет знак:

V₂=32,9−V₁.

Как видно, найти значение V₂ мы пока не можем, т.к. не знаем скорости пловца V₁.

Но для этого нам дано второе уравнение в системе.

Выразим его оттуда.

Получим:

V₁=28,5+V₂.

Нам нужно подставить вместо обозначения V₁ его значение 28,5+V₂ в уравнение:

V₂=32,9−V₁.

Получим:

V₂=32,9−(28,5+V₂);

V₂=32,9−28,5−V₂;

V₂=4,4−V₂;

2V₂=4,4;

V₂=2,2.

В итоге , с какой скоростью по модулю движется река относительно припаркованного возле магазина мотоцикла, мы узнали — 2,2 км/ч.

4. Нахождение времени переплывания реки при движении перпендикулярно к течению реки

Лайнер, двигаясь под углом 90 градусов к течению реки , обладая скоростью 4,3 м/с, переплывает реку шириной 370 м. Скорость течения реки — 2,1 м/с. В ответе укажи время, нужное лайнеру , чтобы переплыть реку.

Шаги решения:

Запишем краткое условие к этой задаче.

Дано:

∣V⃗₁∣=4,3 м/с;

∣V⃗₂∣=2,1 м/с;

|S|=370 м;

|t|−?

Обозначим скорость лайнера V⃗₁, а скорость течения реки V⃗₂.

Покажем на рисунке, как направлены векторы их скоростей.

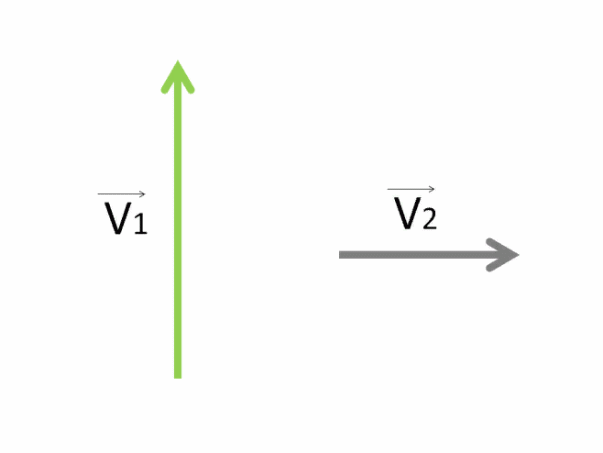
Естественно, лайнер не сможет уже плыть прямо. Течение реки будет действовать вправо и лайнер начнёт смещаться понемногу в ту сторону, куда оно направлено.

Можно показать, конечно, как точно будет направлен результирующий вектор скорости.

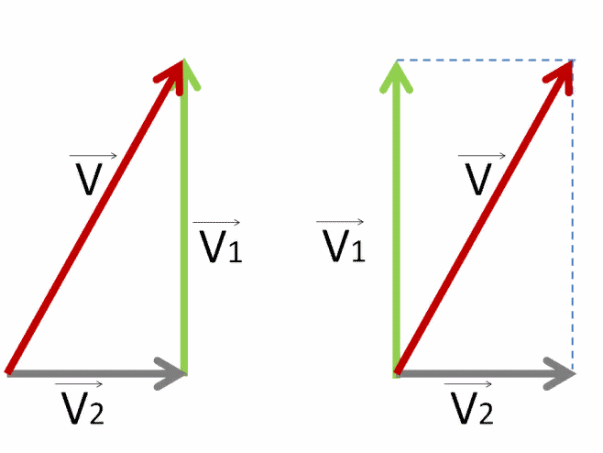
Для этого нужно сложить скорости V⃗₁ и V⃗₂ по правилу треугольника или по правилу параллелограмма.

Правильно это сделать так:

выстраиваем их друг за другом, чтобы получились стороны треугольника

или соединяем начала этих векторов — тогда используем правило параллелограмма.

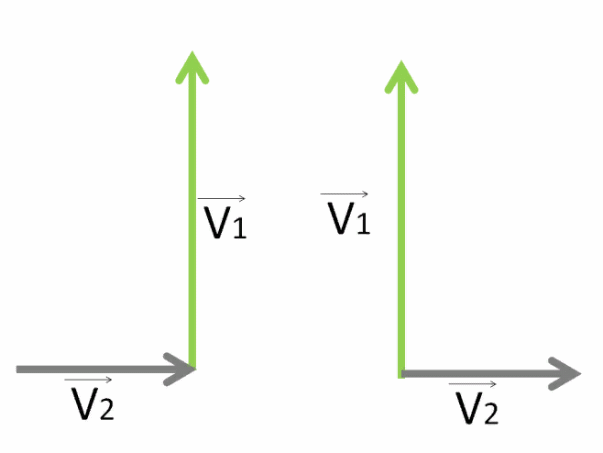
Для сложения по правилу треугольника просто соединяем начало первого вектора с концом последнего.

Для сложения по правилу параллелограмма дорисовываем ещё две стороны напротив уже имеющихся двух.

Должен получиться один и тот же вектор V⃗ . Нарисуем его красным цветом.

Лайнер плывёт, но сносится течением реки.

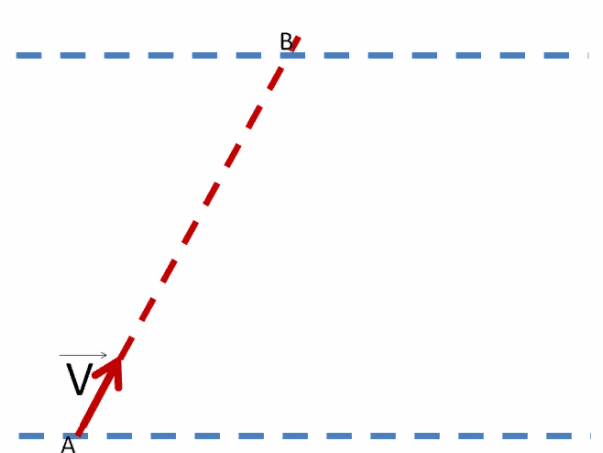
Однако лайнер постоянно стремится переплыть реку со скоростью V⃗₁. Именно с этой скоростью лайнер перемещается к противоположному берегу.

Поэтому в данной задаче нам нужна только скорость лайнера V⃗₁ и ширина реки 370 м.

Чтобы найти время, нужное лайнеру , чтобы переплыть реку, необходимо всё расстояние в 370 м разделить на скорость лайнера V⃗₁.

Получим:

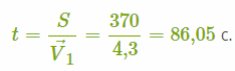
Итак, время, нужное лайнеру , чтобы переплыть реку, составило 86,05c.