Решение задач по теме "Графы"

Решение задач по теме «Графы»

Путь в графе называется циклом , если он начинается и заканчивается в одной и той же вершине.

Теорема 1. Пусть G — ориентированный граф без циклов, x, y и z — три вершины этого графа. Тогда число путей из x в y, проходящих через z, равно p(x, z)p(z, y). В частности, если все пути из x в y проходят через z, то p(x, y) = p(x, z)p(z, y).

Теорема 2. Пусть длины всех рёбер графа G положительны. Тогда если из вершины x есть путь в вершину y, то есть и кратчайший путь из x в y, причём он не содержит циклов.

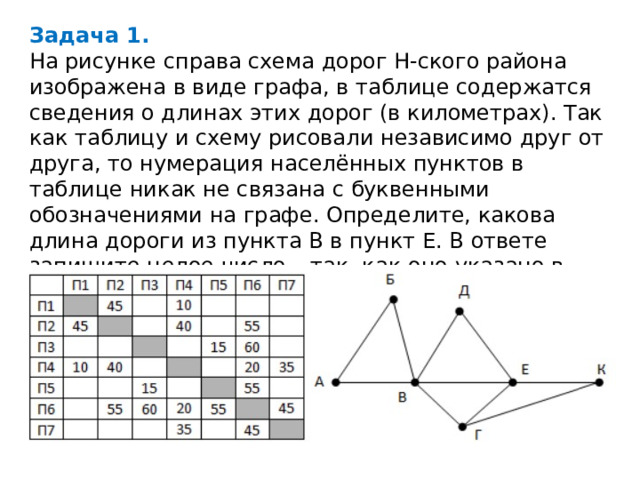
Задача 1.

На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице.

Решение

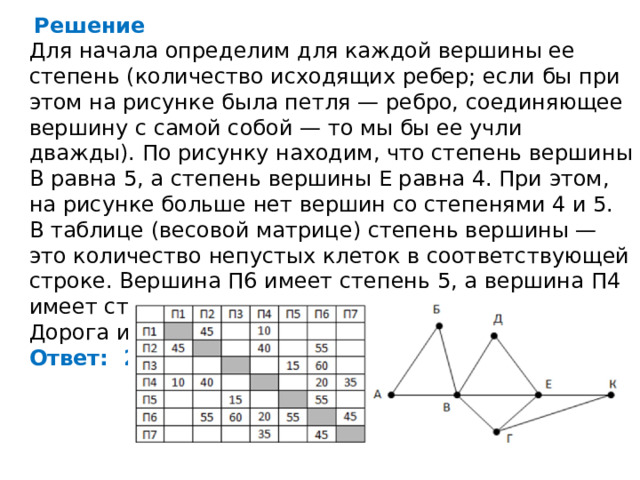
Для начала определим для каждой вершины ее степень (количество исходящих ребер; если бы при этом на рисунке была петля — ребро, соединяющее вершину с самой собой — то мы бы ее учли дважды). По рисунку находим, что степень вершины В равна 5, а степень вершины Е равна 4. При этом, на рисунке больше нет вершин со степенями 4 и 5.

В таблице (весовой матрице) степень вершины — это количество непустых клеток в соответствующей строке. Вершина П6 имеет степень 5, а вершина П4 имеет степень 4, то есть, это и есть вершины В и Е. Дорога из П4 в П6 имеет длину 20.

Ответ:  20

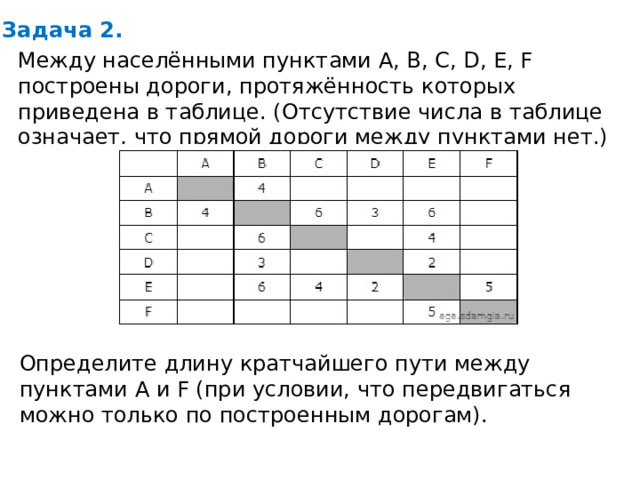
Задача 2.

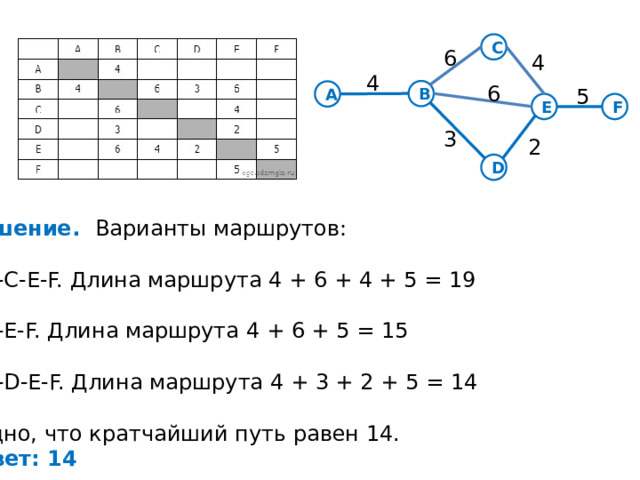
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).

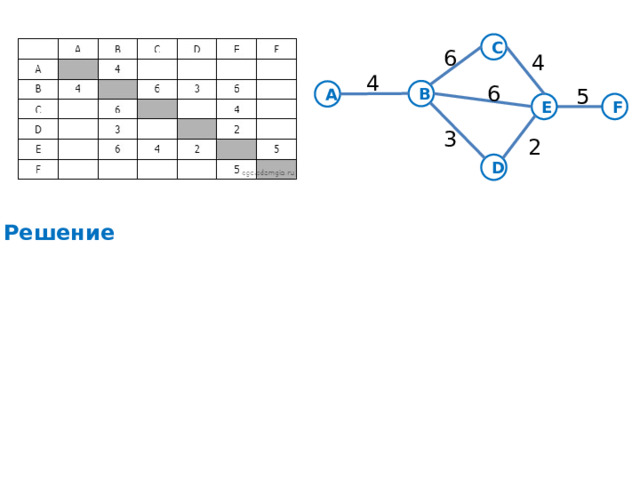
С

6

4

4

6

5

В

А

E

F

3

2

D

Решение

С

6

4

4

6

5

В

А

E

F

3

2

D

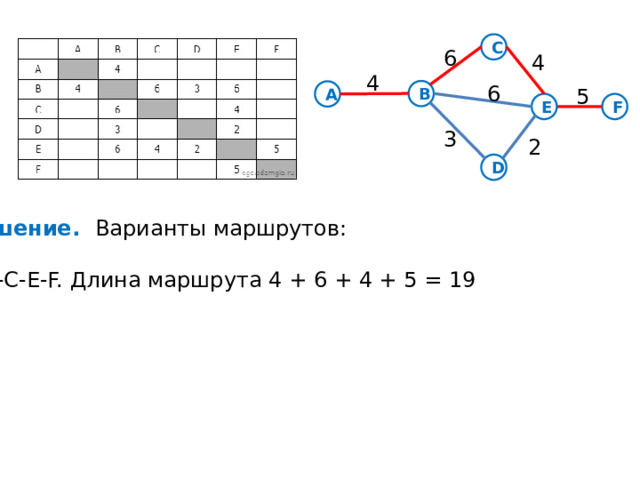
Решение. Варианты маршрутов:

A-B-C-E-F. Длина маршрута 4 + 6 + 4 + 5 = 19

A-B-D-E-F. Длина маршрута 4 + 3 + 2 + 5 = 14

A-B-E-F. Длина маршрута 4 + 6 + 5 = 15

Видно, что кратчайший путь равен 14.

Ответ: 14

С

6

4

4

6

5

В

А

E

F

3

2

D

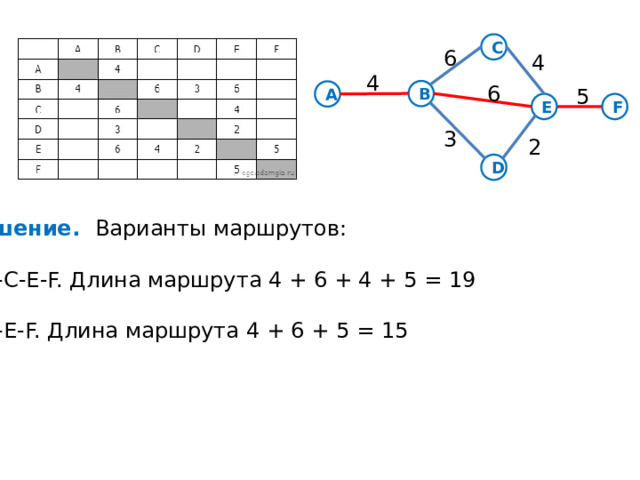
Решение. Варианты маршрутов:

A-B-C-E-F. Длина маршрута 4 + 6 + 4 + 5 = 19

A-B-E-F. Длина маршрута 4 + 6 + 5 = 15

A-B-E-F. Длина маршрута 4 + 6 + 5 = 15

Видно, что кратчайший путь равен 14.

Ответ: 14

С

6

4

4

6

5

В

А

E

F

3

2

D

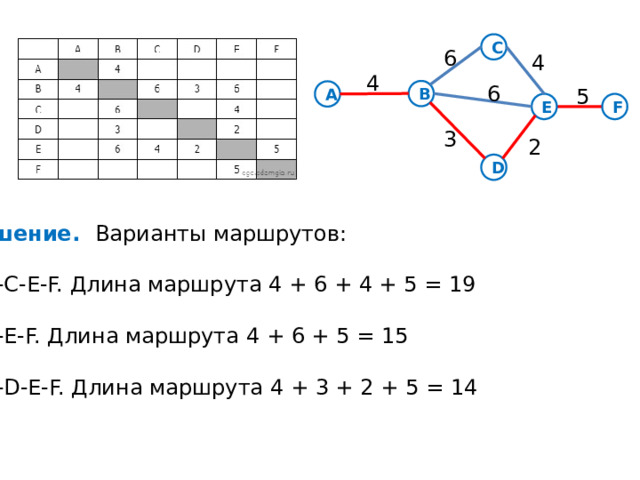
Решение. Варианты маршрутов:

A-B-C-E-F. Длина маршрута 4 + 6 + 4 + 5 = 19

A-B-E-F. Длина маршрута 4 + 6 + 5 = 15

A-B-D-E-F. Длина маршрута 4 + 3 + 2 + 5 = 14

  Ответ: 14

С

6

4

4

6

5

В

А

E

F

3

2

D

Решение. Варианты маршрутов:

A-B-C-E-F. Длина маршрута 4 + 6 + 4 + 5 = 19

A-B-E-F. Длина маршрута 4 + 6 + 5 = 15

A-B-D-E-F. Длина маршрута 4 + 3 + 2 + 5 = 14

Видно, что кратчайший путь равен 14.

Ответ: 14

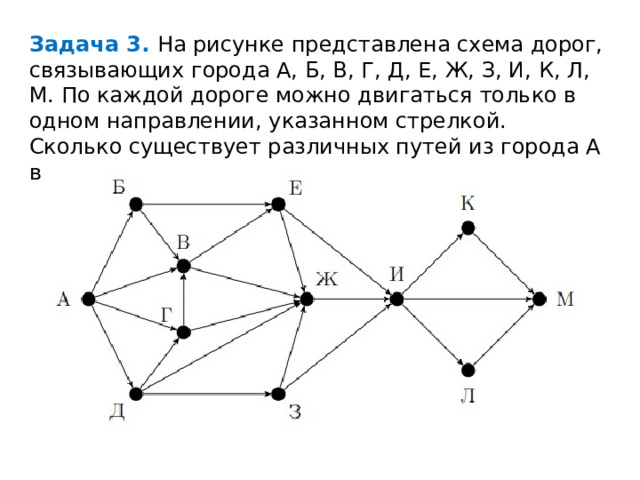
Задача 3. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город В?

Решение

Из рисунка видно, что любой путь из А в М проходит через И. По условию задачи мы должны искать только те пути, которые проходят через В. Обозначим число путей через N.

По теореме 1 N = p(А,В)p(В, И)p(И, М).

Из рисунка видно, что имеется четыре пути из А в В :

(А → Б → В, А → В, А → Г → В, А → Д → Г → В),

три пути из В в И:

(В → Е → И, В → Ж → И, В → Е → Ж → И)

и три пути из И в М: (И → К → М, И → М, И → Л → М).

Получаем N = 4 · 3 · 3 = 36.

Ответ: 36

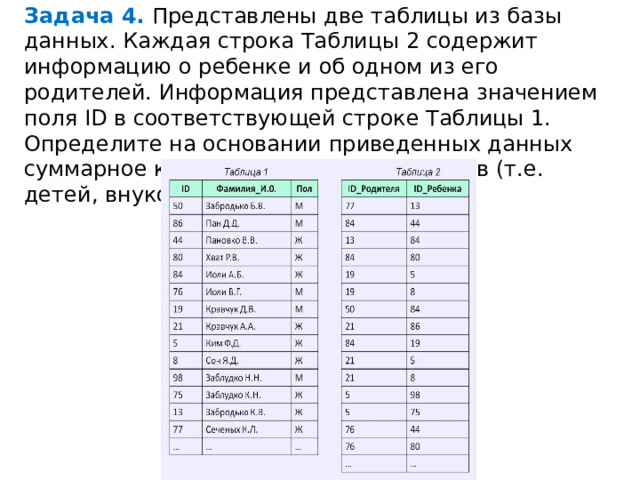
Задача 4. Представлены две таблицы из базы данных. Каждая строка Таблицы 2 содержит информацию о ребенке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке Таблицы 1. Определите на основании приведенных данных суммарное количество прямых потомков (т.е. детей, внуков, правнуков) Иоли А.Б.

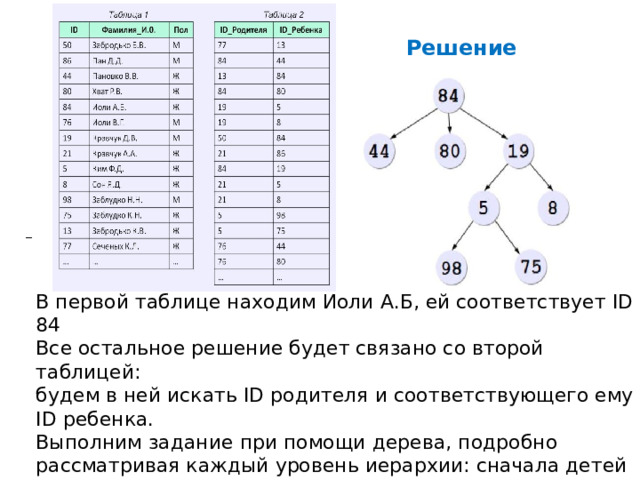
Решение

В первой таблице находим Иоли А.Б, ей соответствует ID 84

Все остальное решение будет связано со второй таблицей:

будем в ней искать ID родителя и соответствующего ему ID ребенка.

Выполним задание при помощи дерева, подробно рассматривая каждый уровень иерархии: сначала детей родителя 84, затем по полученным ID найдем внуков Иоли А.Б, затем правнуков и т.д. Посчитаем общее количество потомков: 7.

Ответ: 7 прямых потомков.

Задача 5. Между населёнными пунктами A, B, C, D, E построены дороги, стоимость перевозки по которым приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет). Определите МАКСИМАЛЬНУЮ стоимость перевозки груза из C в B при условии, что маршрут не может проходить через какой-то пункт более одного раза.

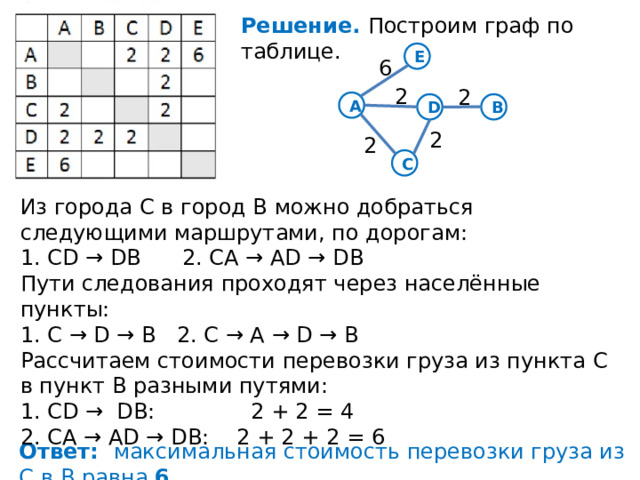
Решение. Построим граф по таблице.

E

6

2

2

А

D

В

2

2

С

Из города C в город B можно добраться следующими маршрутами, по дорогам:

1. CD → DB 2. CA → AD → DB

Пути следования проходят через населённые пункты:

1. C → D → B 2. C → A → D → B

Рассчитаем стоимости перевозки груза из пункта C в пункт B разными путями:

1. CD → DB: 2 + 2 = 4

2. CA → AD → DB: 2 + 2 + 2 = 6

Ответ: максимальная стоимость перевозки груза из С в В равна 6