Решение задач по теме "Пирамида"

№ 1

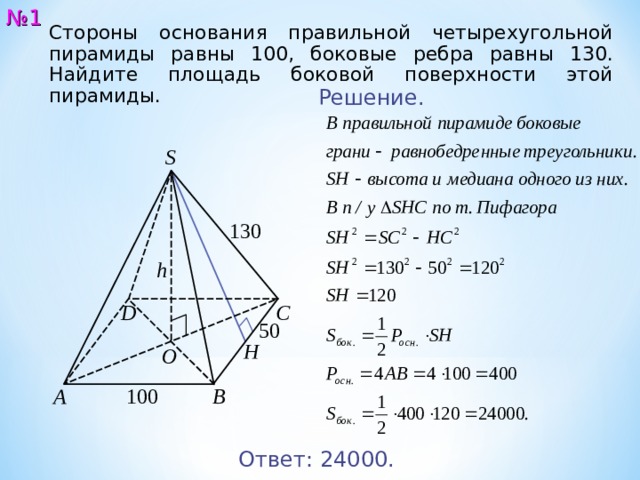
Стороны основания правильной четырехугольной пирамиды равны 100, боковые ребра равны 130. Найдите площадь боковой поверхности этой пирамиды.

Решение.

S

130

h

D

С

50

Н

O

A

100

B

Ответ: 24 000.

2

№ 2

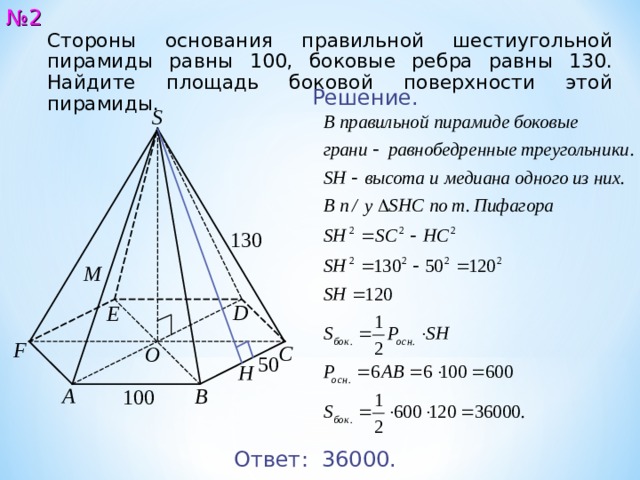
Стороны основания правильной шестиугольной пирамиды равны 100, боковые ребра равны 130. Найдите площадь боковой поверхности этой пирамиды.

Решение.

S

13 0

M

D

E

F

C

O

50

Н

A

B

10 0

Ответ: 360 00.

3

№ 3

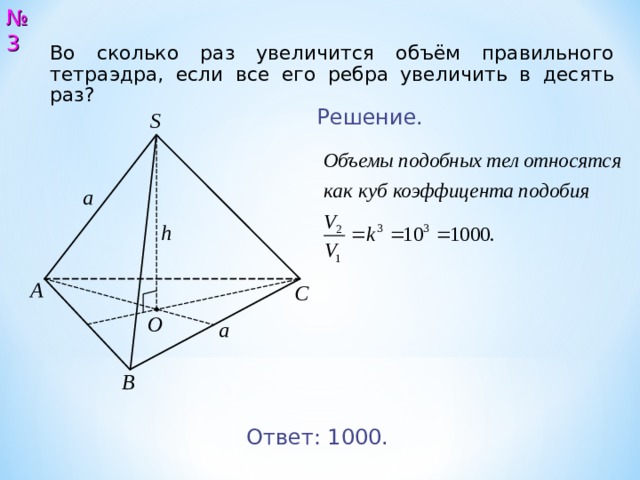
Во сколько раз увеличится объём правильного тетраэдра, если все его ребра увеличить в десять раз?

Решение.

S

a

h

А

С

O

a

В

Ответ: 1000.

4

№ 4

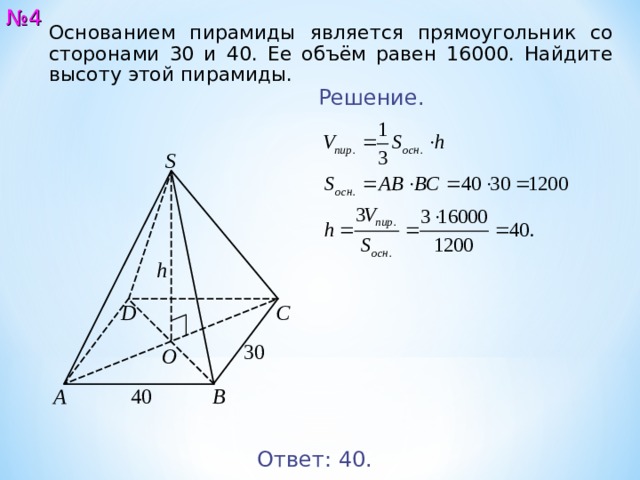
Основанием пирамиды является прямоугольник со сторонами 30 и 40. Ее объём равен 16000. Найдите высоту этой пирамиды.

Решение.

S

h

С

D

30

O

A

B

40

Ответ: 4 0.

5

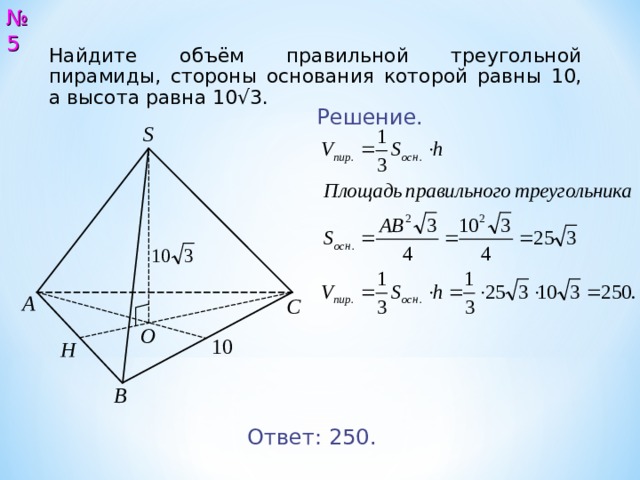
№ 5

Найдите объём правильной треугольной пирамиды, стороны основания которой равны 10, а высота равна 10√3.

Решение.

S

А

С

O

10

H

В

Ответ: 250.

6

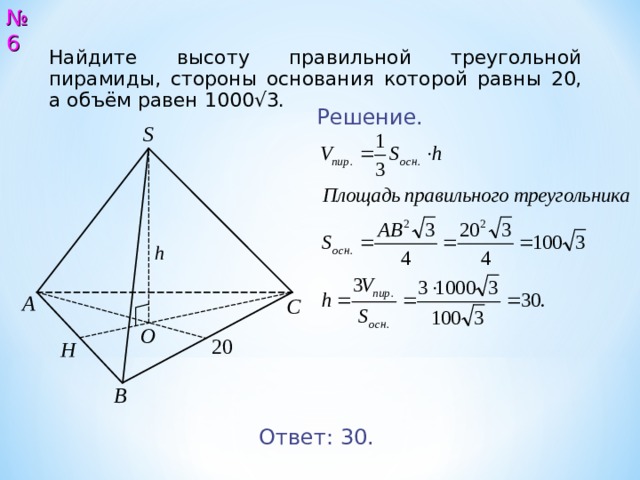
№ 6

Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 20, а объём равен 10 00 √3.

Решение.

S

А

С

O

2 0

H

В

Ответ: 3 0.

7

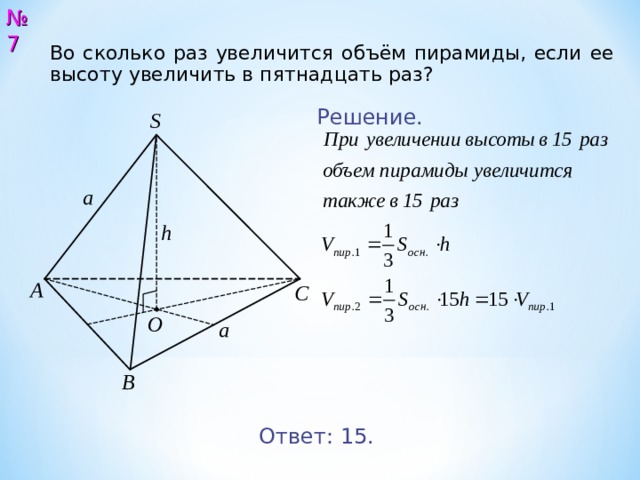
№ 7

Во сколько раз увеличится объём пирамиды, если ее высоту увеличить в пятнадцать раз?

Решение.

S

a

h

А

С

O

a

В

Ответ: 15.

8

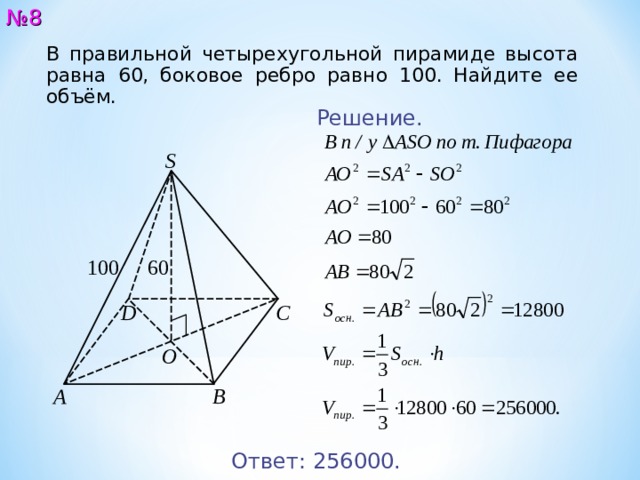
№ 8

В правильной четырехугольной пирамиде высота равна 60, боковое ребро равно 100. Найдите ее объём.

Решение.

S

60

100

С

D

O

A

B

Ответ: 25600 0.

9

№ 9

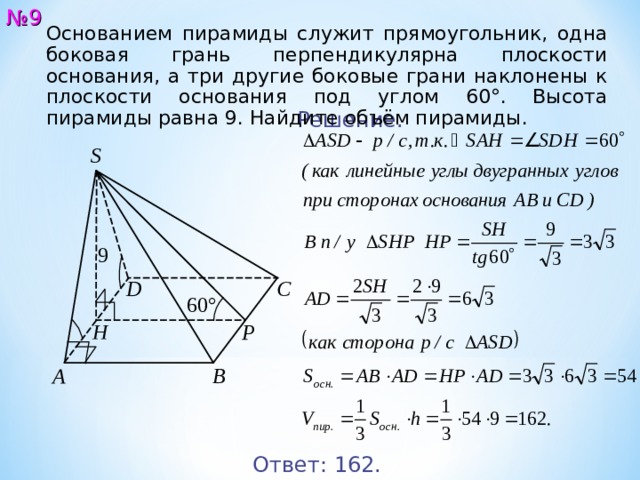
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 9. Найдите объём пирамиды.

Решение.

S

9

D

С

60°

Р

Н

A

B

Ответ: 162 .

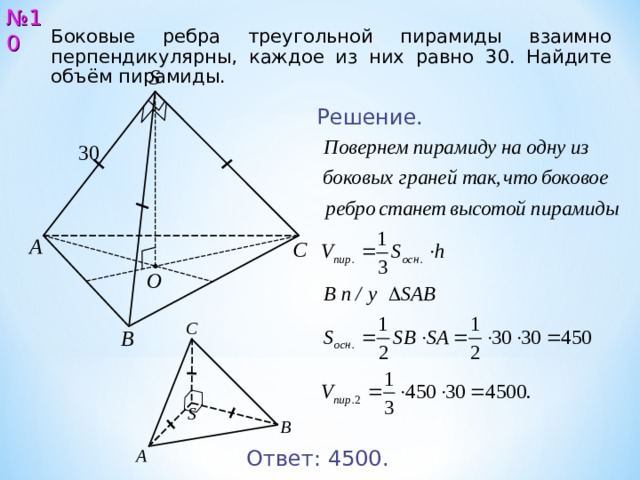
№ 10

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3 0 . Найдите объём пирамиды.

S

Решение.

30

А

С

O

С

В

S

В

А

Ответ: 4 5 00 .

11

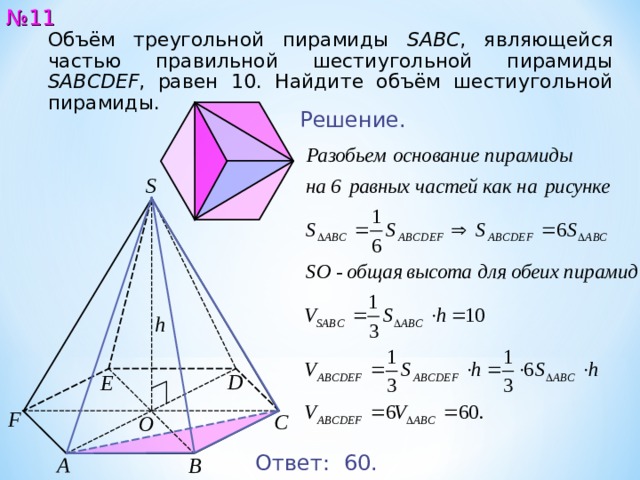
№ 11

Объём треугольной пирамиды SABC , являющейся частью правильной шестиугольной пирамиды SABCDEF , равен 1 0 . Найдите объём шестиугольной пирамиды.

Решение.

S

h

D

E

F

C

O

Ответ: 60 .

A

B

12

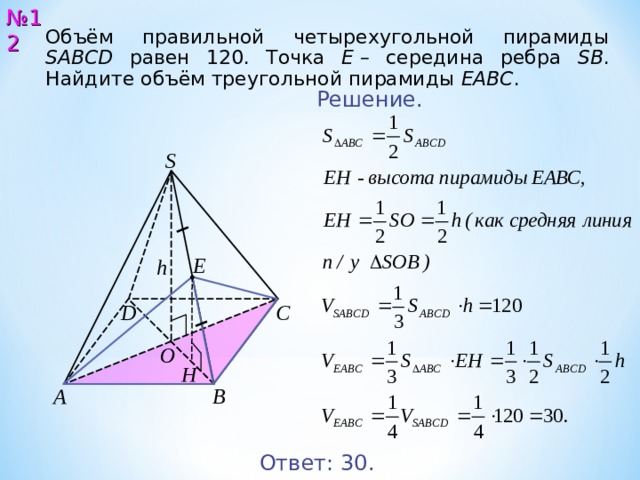
№ 12

Объём правильной четырехугольной пирамиды SABCD равен 12 0 . Точка E  – середина ребра SB . Найдите объём треугольной пирамиды EABC .

Решение.

S

Е

h

С

D

O

Н

A

B

Ответ: 3 0.

13

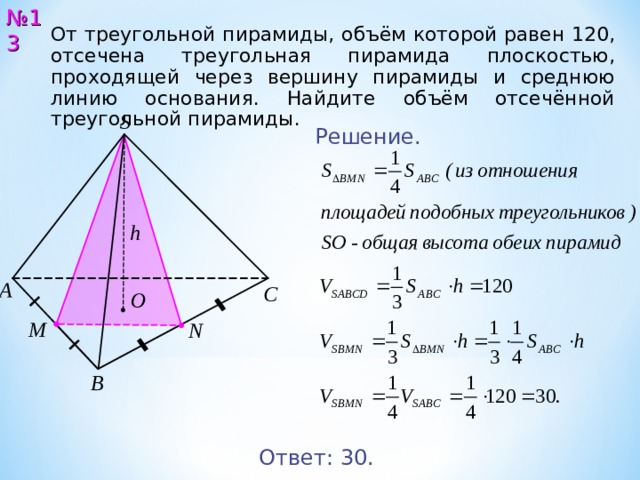
№ 13

От треугольной пирамиды, объём которой равен 120, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объём отсечённой треугольной пирамиды.

S

Решение.

h

А

С

O

M

N

В

Ответ: 30 .

14

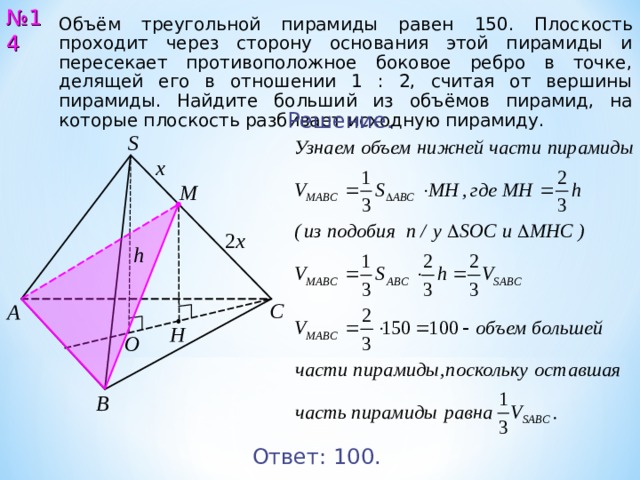
№ 1 4

Объём треугольной пирамиды равен 150. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.

Решение.

S

х

M

2 х

h

С

А

Н

O

В

Ответ: 10 0 .

15

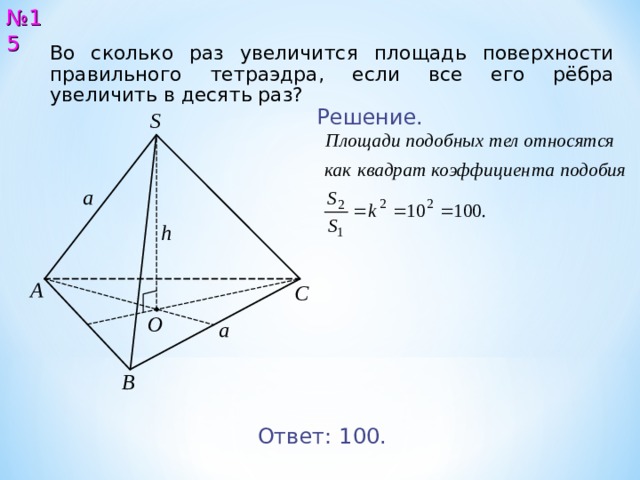
№ 15

Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его рёбра увеличить в десять раз?

Решение.

S

a

h

А

С

O

a

В

Ответ: 1 00 .

16

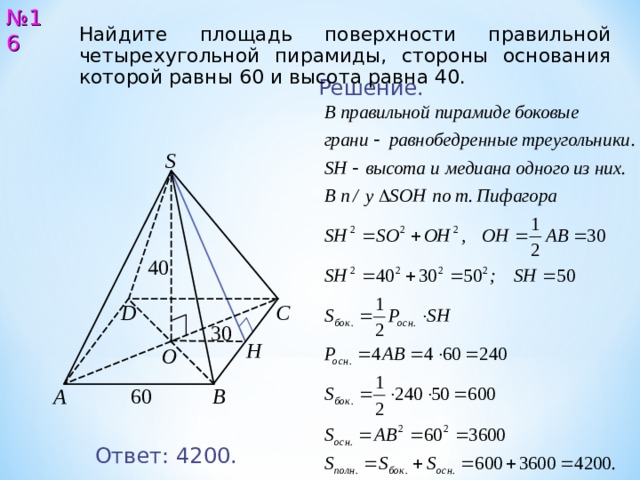
№ 16

Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 0 и высота равна 4 0 . 

Решение.

S

4 0

С

D

3 0

Н

O

6 0

B

A

Ответ: 420 0.

17

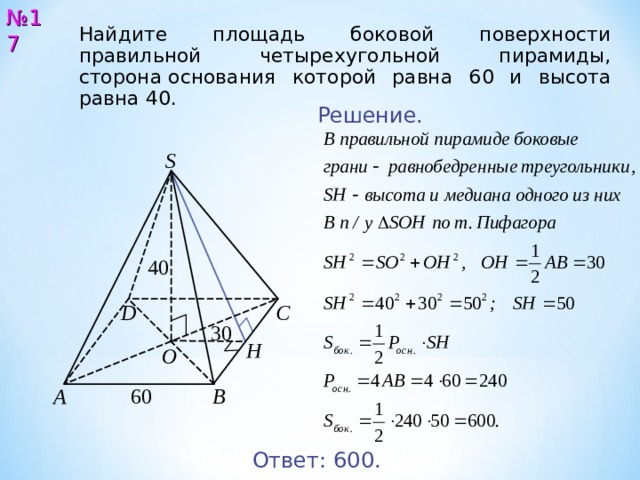
№ 17

Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 0 и высота равна 4 0 .

Решение.

S

4 0

С

D

3 0

Н

O

6 0

B

A

Ответ: 60 0.

18

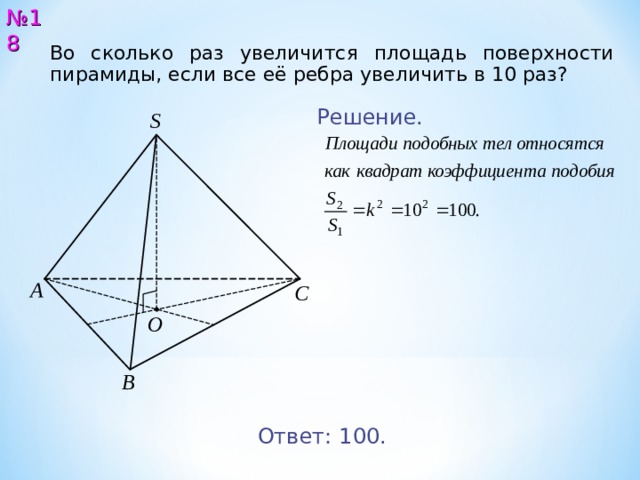
№ 1 8

Во сколько раз увеличится площадь поверхности пирамиды, если все её ребра увеличить в 10 раз?

Решение.

S

А

С

O

В

Ответ: 1 00 .

19

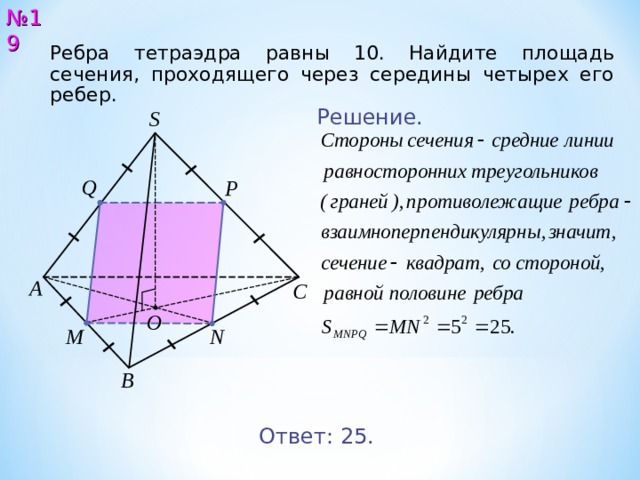
№ 1 9

Ребра тетраэдра равны 1 0 . Найдите площадь сечения, проходящего через середины четырех его ребер.

Решение.

S

Q

P

А

С

O

M

N

В

Ответ: 25.

20

№ 20

Найдите объём пирамиды, высота которой равна 60, а основание – прямоугольник со сторонами 30 и 40.

Решение.

S

60

С

D

30

O

A

B

40

Ответ: 2 4 0 0.

21

№ 21

В правильной четырехугольной пирамиде высота равна 120, объём равен 20 0 00. Найдите боковое ребро этой пирамиды.

Решение.

S

120

D

С

O

B

A

Ответ: 13 0.

22

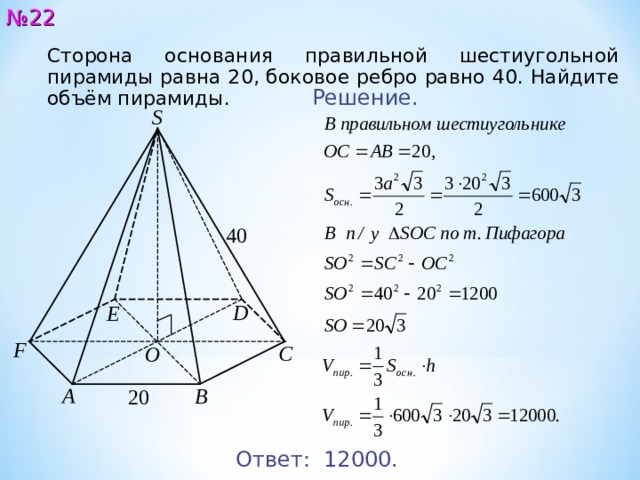
№ 22

Сторона основания правильной шестиугольной пирамиды равна 2 0 , боковое ребро равно 4 0 . Найдите объём пирамиды.

Решение.

S

4 0

D

E

F

C

O

A

B

2 0

Ответ: 12000.

23

№ 2 3

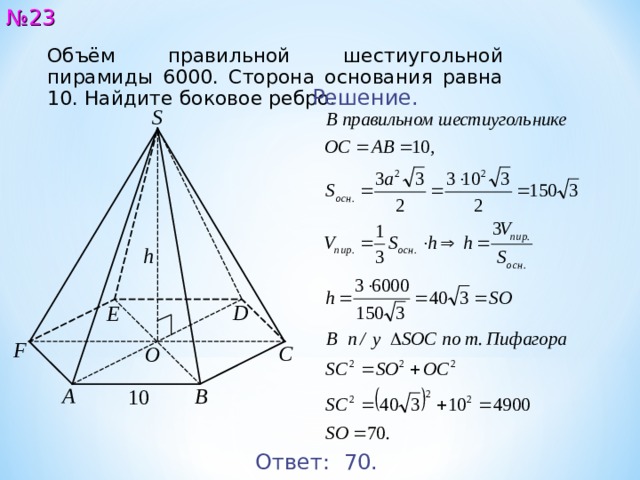
Объём правильной шестиугольной пирамиды 60 0 0. Сторона основания равна 10. Найдите боковое ребро.

Решение.

S

h

D

E

F

C

O

A

B

1 0

Ответ: 7 0.

24

№ 24

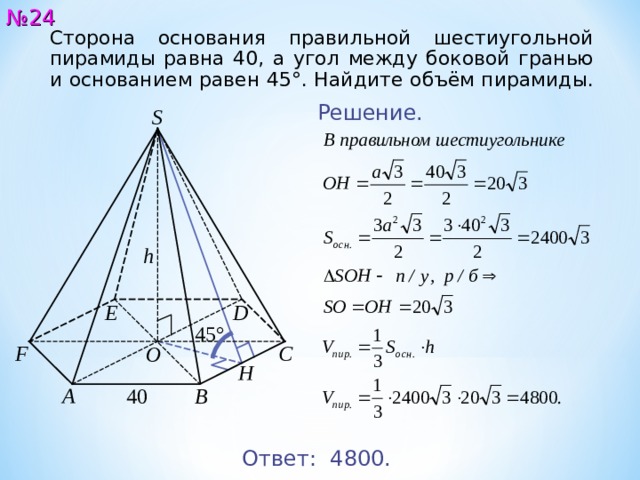
Сторона основания правильной шестиугольной пирамиды равна 4 0 , а угол между боковой гранью и основанием равен 45°. Найдите объём пирамиды.

Решение.

S

h

E

D

45°

C

F

O

Н

A

4 0

B

Ответ: 480 0.

25

№ 2 5

Объём параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 12 0 . Найдите объём треугольной пирамиды B 1 ABC .

Решение.

D 1

C 1

B 1

A 1

C

D

B

A

Ответ: 2 0.

26

№ 2 6

Объём куба равен 12000. Найдите объём четырехугольной пирамиды, основанием которой является грань куба, а вершиной – центр куба.

Решение.

C 1

D 1

A 1

B 1

М

C

D

A

B

Ответ: 2 0 00 .

27

№ 2 7

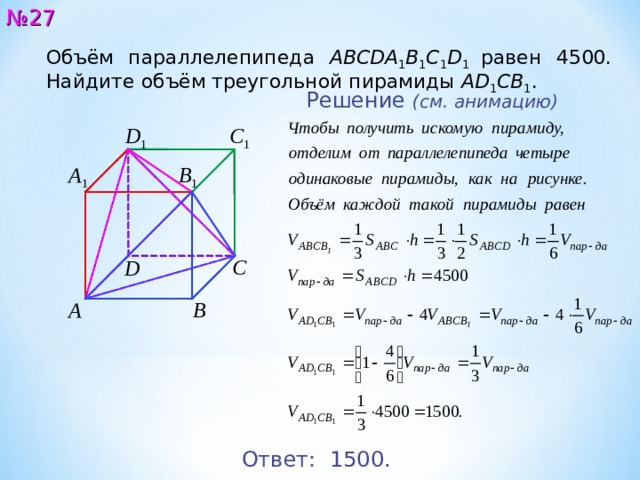
Объём параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 45 00 . Найдите объём треугольной пирамиды AD 1 CB 1 .

Решение ( см. анимацию )

C 1

D 1

B 1

A 1

C

D

B

A

Ответ: 15 00 .

27

№ 2 8

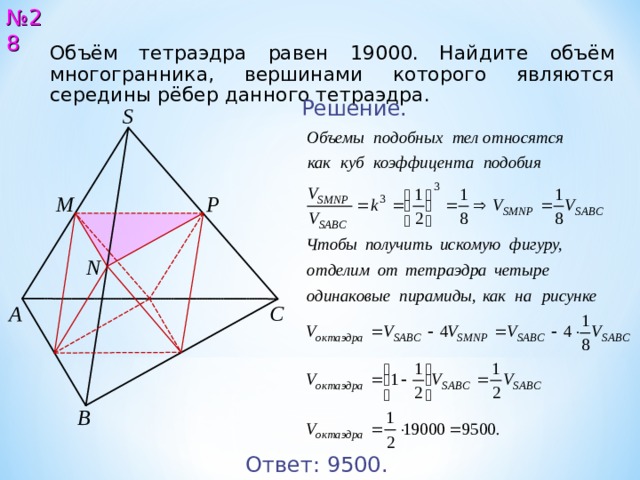
Объём тетраэдра равен 19 000 . Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.

Решение.

S

М

P

N

С

А

В

Ответ: 9500 .

29

№ 2 9

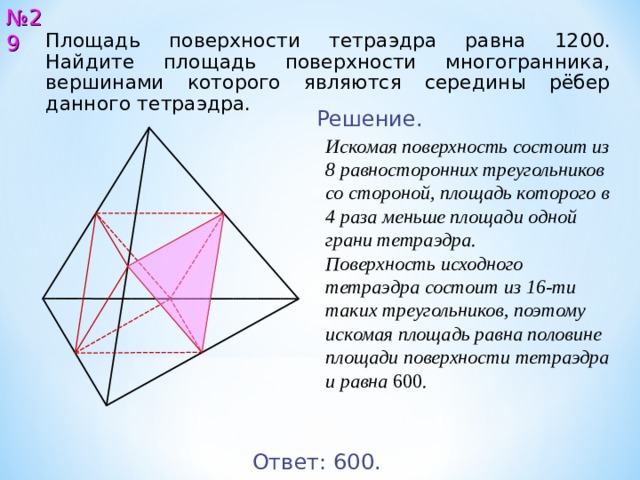
Площадь поверхности тетраэдра равна 12 00 . Найдите площадь поверхности многогранника, вершинами которого являются середины рёбер данного тетраэдра.

Решение.

Искомая поверхность состоит из 8 равносторонних треугольников со стороной, площадь которого в 4 раза меньше площади одной грани тетраэдра.

Поверхность исходного тетраэдра состоит из 16-ти таких треугольников, поэтому искомая площадь равна половине площади поверхности тетраэдра и равна 600 .

Ответ: 600 .

29

№ 30

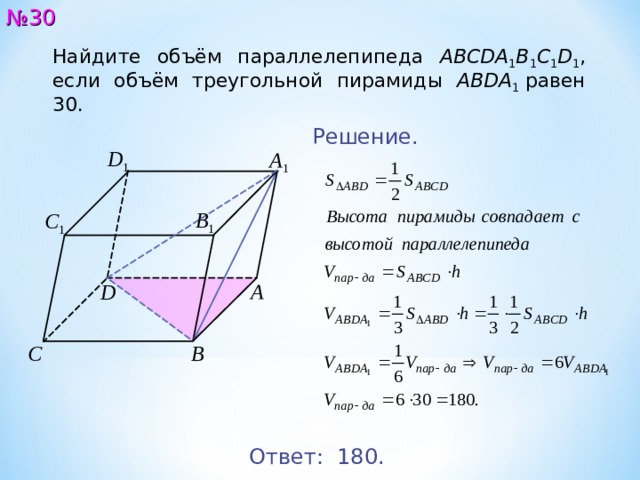
Найдите объём параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объём треугольной пирамиды ABDA 1  равен 30.

Решение.

D 1

A 1

B 1

C 1

A

D

B

C

Ответ: 18 0.

31

№ 3 1

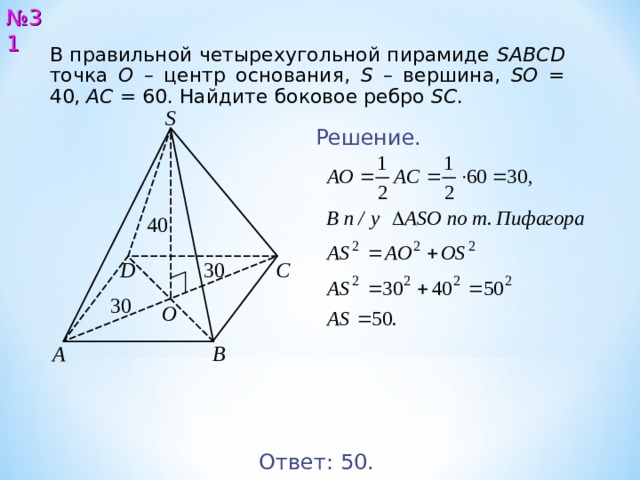
В правильной четырехугольной пирамиде SABCD точка О – центр основания, S – вершина, SO = 4 0 , AC = 6 0 . Найдите боковое ребро SC .

S

Решение.

4 0

3 0

С

D

3 0

O

A

B

Ответ: 5 0.

32

№ 32

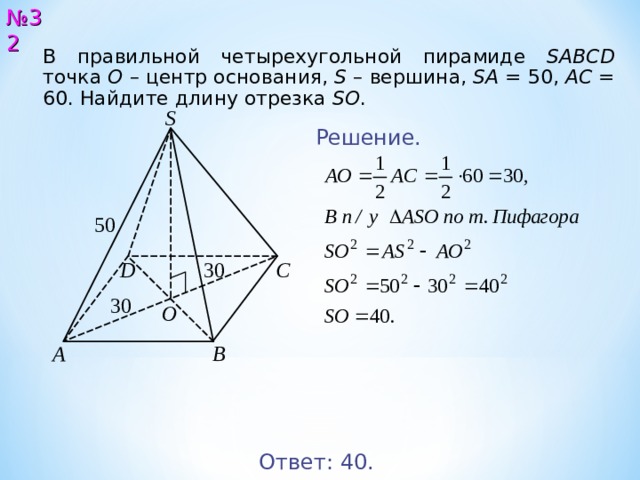
В правильной четырехугольной пирамиде SABCD точка О  – центр основания, S – вершина, SA = 5 0 , AC = 6 0 . Найдите длину отрезка SO .

S

Решение.

5 0

3 0

С

D

3 0

O

A

B

Ответ: 4 0.

33

№ 33

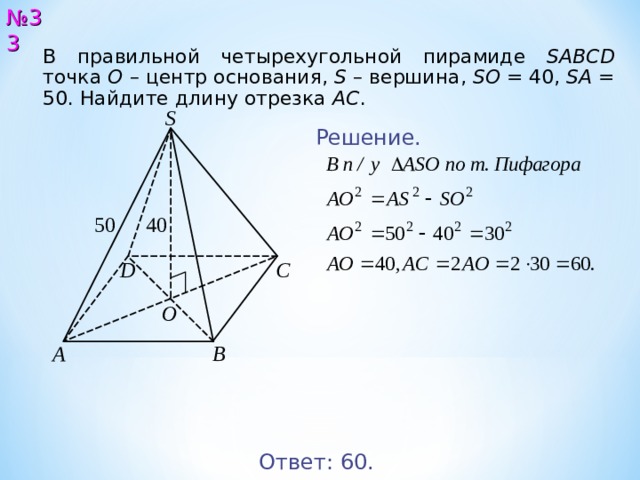
В правильной четырехугольной пирамиде SABCD точка О  – центр основания, S – вершина, SO = 4 0 , SA = 5 0 . Найдите длину отрезка AC .

S

Решение.

5 0

4 0

D

С

O

B

A

Ответ: 6 0.

34

№ 3 4

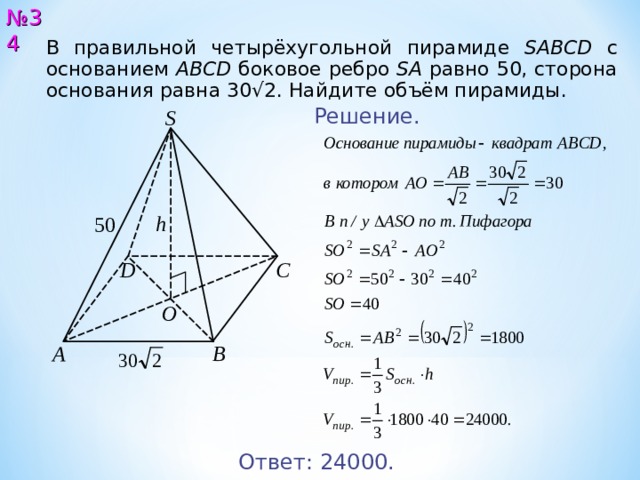
В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SA равно 50, сторона основания равна 30√2. Найдите объём пирамиды.

Решение.

S

h

5 0

D

С

O

A

B

Ответ: 2400 0.

35

№ 35

В правильной четырёхугольной пирамиде все рёбра равны 1 0 . Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

S

Решение.

Q

P

N

M

С

D

O

1 0

A

B

Ответ: 2 5.

36

№ 3 6

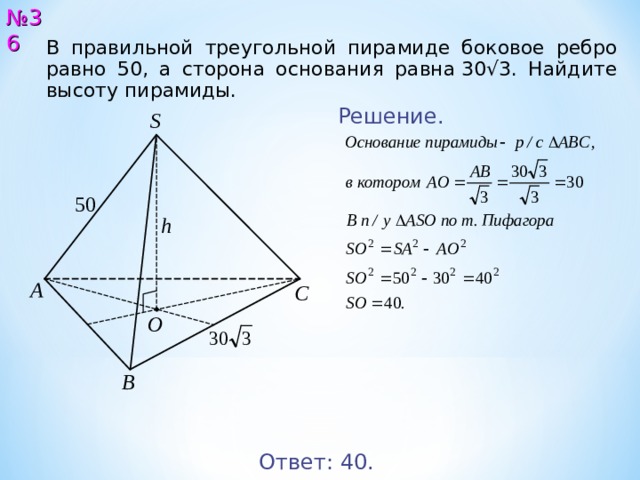
В правильной треугольной пирамиде боковое ребро равно 50, а сторона основания равна 30√3. Найдите высоту пирамиды.

Решение.

S

5 0

h

А

С

O

В

Ответ: 40 .

37