Решение задач по теме закон сохранения энергии

Закон сохранения энергии

Закон сохранения энергии

• Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, работа которых не зависит от траектории движения тела.

• К таким силам относятся силы тяготения и силы упругости.

• Сила трения не является консервативной.

• Границы применимости

Обоснование №1

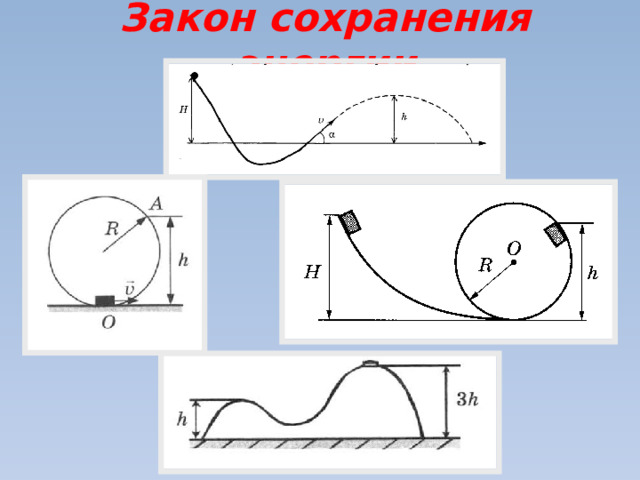
Задачу будем решать в инерциальной системе отсчета, связанной с Землей. Шайбу будем считать материальной точкой. Трение о воздух пренебрежимо мало. Выберем механическую систему тел «шайба-Земля». При движении на шайбу действуют сила тяжести и сила нормальной реакции опоры. Сила нормальной реакции опоры работу не совершает, т.к. направлена перпендикулярно перемещению шайбы. Поэтому работа внешних сил равна нулю.

Закон сохранения механической энергии системы выполняется.

Обоснование №2

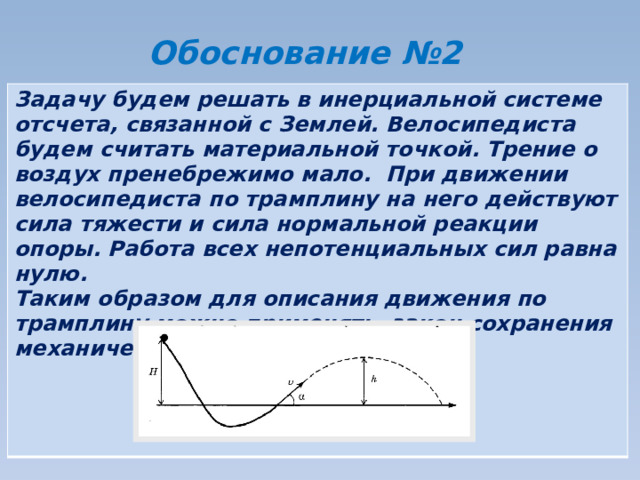
Задачу будем решать в инерциальной системе отсчета, связанной с Землей. Велосипедиста будем считать материальной точкой. Трение о воздух пренебрежимо мало. При движении велосипедиста по трамплину на него действуют сила тяжести и сила нормальной реакции опоры. Работа всех непотенциальных сил равна нулю.

Таким образом для описания движения по трамплину можно применять закон сохранения механической энергии.

Обоснуйте применимость закона сохранения энергии к данному случаю.

Обоснуйте применимость закона сохранения энергии к данному случаю.

Задачу будем решать в инерциальной системе отсчета, связанной с Землей. Шайбу и горку (движется поступательно) будем считать материальными точками. Трение в системе отсутствует. Работа всех непотенциальных сил равна нулю. Следовательно к этой системе тел можно применить закон сохранения механической энергии.

Динамика. Законы Ньютона.

• В инерциальной системе отсчета поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действие других тел скомпенсировано.

F=0, a=0, v=const

2) Ускорение, приобретаемое телом, прямо пропорционально приложенной силе и обратно пропорционально массе этого тела.

F = ma

3) Силы, с которыми тела взаимодействуют равны по модулю, а направлены вдоль одной прямой в противоположные стороны.

F 12 = F 21

Динамика. Законы Ньютона.

Границы применимости законов Ньютона

Законы классической механики, сформулированные Ньютоном,

Они становятся неточными , если

описывают движения материальных точек относительно  инерциальных систем отсчета .

• тела и системы начинают двигаться очень быстро, со скоростями порядка скорости света 

с ≅ 300000 км/с 

2) тела и системы становятся слишком малыми, порядка размеров атомов  r≅1нм (в этом случае процессы становятся квантовыми).

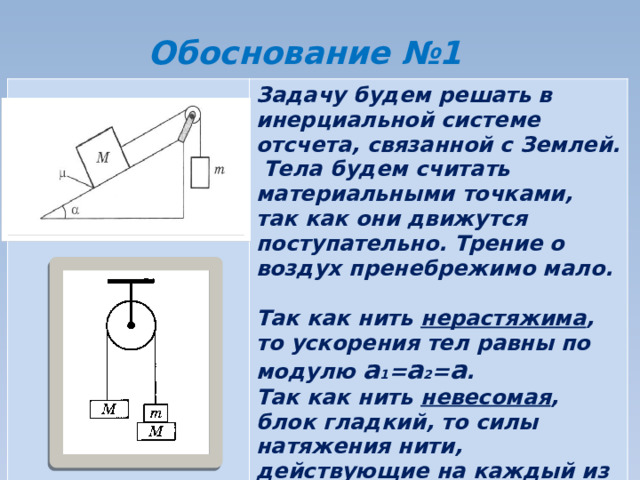
Обоснование №1

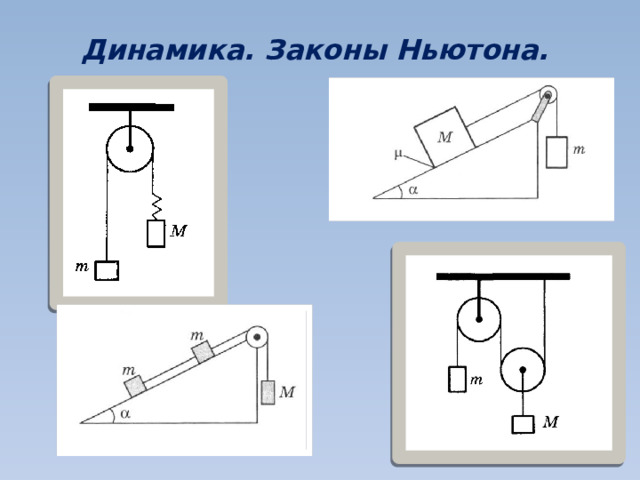
Задачу будем решать в инерциальной системе отсчета, связанной с Землей. Тела будем считать материальными точками, так как они движутся поступательно. Трение о воздух пренебрежимо мало.

Так как нить нерастяжима , то ускорения тел равны по модулю а 1 = а 2 = а .

Так как нить невесомая , блок гладкий, то силы натяжения нити, действующие на каждый из брусков одинаковы: Т 1 =Т 2 =Т.

Обоснуйте применимость используемых законов к решению задачи

Обоснуйте применимость используемых законов к решению задачи

Задачу будем решать в инерциальной системе отсчета , связанной с Землей. Тела будем считать материальными точками, так как их движение поступательное. Трением о воздух пренебрежём. На рисунке показаны силы, действующие на гирю и груз. Так как тела движутся по условию с постоянным ускорением, значит силы, действующие на них постоянные и длина пружины не меняется при движении.

Так как нити нерастяжимые а длина пружины постоянная, то ускорения тел равны по модулю и направлены в противоположные стороны: а1=а2=а.

Так как блок и нити невесомые , а трение отсутствует, то модули сил натяжения нити, действующие на гирю и пружины одинаковые: Т1=Т2 =Т .

Так как пружина легкая, то Т=Fупр .

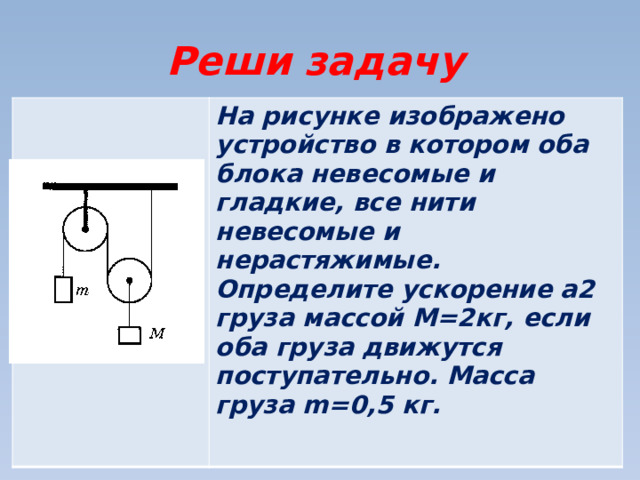
Реши задачу

На рисунке изображено устройство в котором оба блока невесомые и гладкие, все нити невесомые и нерастяжимые. Определите ускорение а2 груза массой М=2кг, если оба груза движутся поступательно. Масса груза m=0,5 кг.

Спасибо за внимание