МУНИЦИПАЛЬНОЕ КАЗЁННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
НЕВОНСКАЯ ШКОЛА
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ГРАФОВ
Районная учебно-исследовательская конференция
(исследовательская работа)
Выполнила:
учащаяся 8 класса,
МКОУ Невонской школы
Алина Николаевна Бутакова
Руководитель:
учитель математики
МКОУ Невонской школы
Татьяна Серафимовна Летунова
п. Невонка. 2019 г.
ВВЕДЕНИЕ
Актуальность темы заключается в том, что благодаря применению теории графов открывается широкая возможность использования оригинальных и в то же время, очень простых способов решения задач.
Социальная значимость этой работы в том, что в результате применения теории графов расширяется кругозор математических знаний, изменяются взгляды на математику и развивается умение применять математику в реальной жизни.
Научная новизна. Решение многих задач упрощается, если удается использовать графы, а представление данных в виде графа придает им наглядность и простоту.
Объектом исследования является теория графов и ее приложения.
Предметом исследования выбраны задачи с использованием графов при решении.
Цель работы: Научиться строить графы и решать с их помощью задачи.
Для достижения поставленной цели определила следующие задачи:
1. Изучить научно-популярную литературу по данной теме.
2. Применить теорию графов при решении задач.
3. Решить несколько видов задач.
4. Показать связь с другими областями знаний.
Разработанность проблемы.
Первая работа по теории графов, принадлежащая известному швейцарскому математику Л.Эйлеру, появилась в 1736 г. Вначале теория графов казалась довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Очень долго она находилась в стороне от главных направлений исследований ученых. Толчок к развитию теория графов получила на рубеже ХIX и ХХ столетий, когда резко возросло число работ в области топологии и комбинаторики, с которыми ее связывают самые тесные узы родства. Графы стали использоваться при построении схем электрических цепей и молекулярных схем. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кенига в 30-е годы ХХ столетия. [9]. В последнее время графы и связанные с ними методы исследований пронизывают на разных уровнях едва ли не всю современную математику. Графы эффективно используются в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине, географии. Широкое применение находят графы в таких областях, как программирование, электроника, в решении вероятностных и комбинаторных задач и др. Математические развлечения и головоломки тоже являются частью теории графов. В настоящее время эта теория находит многочисленное применение в разнообразных практических вопросах: при установлении разного рода соответствий, при решении транспортных задач, задач о потоках в сети нефтепроводов, в теории передачи сообщений. Теория графов теперь применяется и в таких областях, как экономика, психология, информатика, биология и физика.
Постановка и формулировка проблемы: Очень часто в жизни встречаются задачи, которые логически и просто по действиям решить нельзя! Я увидела, что такие задачи можно решить с помощью построения графа. Мне стало интересно, и я решила изучить теорию графов и научиться решать некоторые задачи с их помощью.
Гипотезой исследования данной работы является следующее предположение, что решение задач по различным предметам упрощается, если удается использовать теорию графов.
План исследования:
-
Изучить научно-популярную литературу по теории графов.
-
Разобрать решение некоторых задач на применение теории графов.
-
Решить несколько задач, применяя закономерности Эйлера.
-
Выбрать и решить несколько задач, встречающихся в математике 5-9 классов.
-
Решить задачи с использованием информационных моделей на графах.
-
Решить логическую задачу с помощью граф.
В исследовании были использованы следующие методы:
Теоретические:
1) Изучение литературы по теории графов
2) Анализ и обобщение изученной информации
Эмпирические:
1) Решение логических задач
2) Подбор задач
Практическая значимость
Полученная информация по результатам исследовательской работы может быть использована на факультативных занятиях и элективных курсах по различным учебным предметам (биология, информатика, география, химия), при подготовке к ЕГЭ по математике и информатике.
Глава I. ТЕОРИЯ «ГРАФОВ»
-
Понятие графа. Виды графов
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» - пишу. В математике определение графа дается так: графом называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами графа, а соединяющие линии – рёбрами. Примерами графов могут служить схемы авиалиний, метро, дорог, электросхемы, чертежи многоугольников. Использует графы и дворянство. Например, в генеалогическом дереве вершины – члены рода, а связывающие их отрезки – отношения родственности. Первая работа по теории графов принадлежит Леонарду Эйлеру, хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг [1,5,6]. Граф, состоящий из «изолированных» вершин, называется нулевым графом. (рис.1) Графы, в которых не построены все возможные ребра, называются неполными графами. (рис.2) Графы, в которых построены все возможные ребра, называются полными графами. (рис3). [1,2,5]
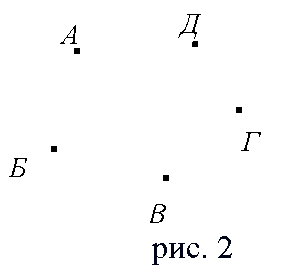
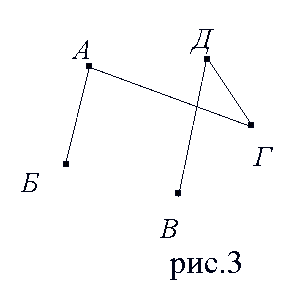
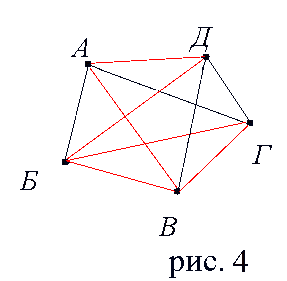
Рис.1 Рис.2 Рис.3
Граф, в котором линии направленные, называется ориентированным графом. Две вершины, соединенные дугой или ребрами, называются смежными.
Размеченный (взвешенный) граф – это граф, в котором с вершинами или с линиями связана некоторая дополнительная информация. Эта информация называется весом вершины или линии. Вес задается в виде надписи на вершине или линии, цвет, форма вершины, толщина, цвет или тип линии.
Понятие графа проще всего выяснить на примере:
Задача.
В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводится по круговой схеме – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и Еленой; Борис, как уже говорилось, с Андреем и ещё с Галиной; Виктор – с Галиной, Дмитрием и Еленой; Галина – с Андреем и Борисом; Дмитрий – с Виктором и Елена – с Андреем и Виктором. Сколько игр проведено к настоящему моменту и сколько ещё осталось?
Решение.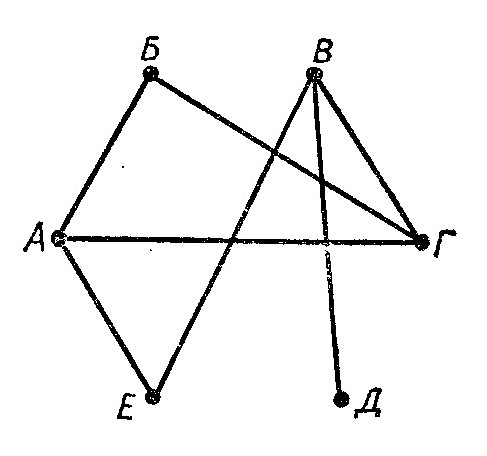
Изобразим данные задачи в виде схемы:
Участников будем изображать точками: Андрея –
Точкой А, Бориса – точкой Б и т.д.
Если двое участников уже сыграли между собой,
Рис.4 то будем соединять изображающие их точки отрезками.
Получается схема, показанная на рисунке 4. Такие схемы называются графами. Точки А, Б, В, Г, Д, Е – вершинами графа, соединяющие их отрезки – рёбрами графа. Важно отметить, что точки пересечения рёбер не являются его вершинами.
Чтобы не возникло путаницы, вершины графа часто изображают не точками, а маленькими кружочками. Рёбра зачастую оказывается удобнее изображать не прямолинейными отрезками, а криволинейными - «дугами».
Продолжим решение задачи.
Ч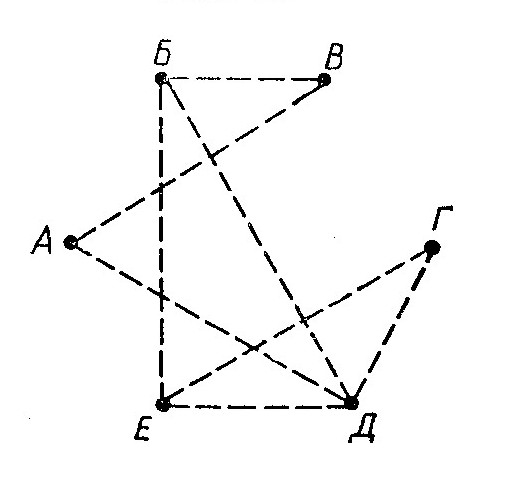 исло игр, проведённых к данному моменту, равно числу рёбер, то есть 7.
исло игр, проведённых к данному моменту, равно числу рёбер, то есть 7.
Чтобы найти число игр, которые осталось провести, построим ещё один граф с теми же вершинами, рёбрами будем соединять тех участников, которые ещё не играли друг с другом:
Рёбер у этого графа оказалось 8, значит осталось провести 8 игр: Андрей должен сыграть в теннис с Виктором и Дмитрием; Борис – с Виктором, Дмитрием и Еленой и т.д.
-
Закономерности Эйлеровских графов.
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. (рис 5)
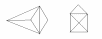
Рис.5
Такими графы названы в честь учёного Леонарда Эйлера.
Закономерность1. Невозможно начертить граф с нечетным числом нечетных вершин.
Закономерность 2. Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
Закономерность 3. Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
Закономерность 4. Граф, имеющий более двух нечетных вершин, невозможно построить «одним росчерком».
Фигура (граф), которую можно начертить, не отрывая карандаш от бумаги, называется уникурсальной.
Теорема. Граф является эйлеровым тогда и только тогда, когда он связан и имеет не более двух нечетных вершин. [5,3]
Доказательство:
Рисуя граф, в каждую вершину, за исключением начальной и конечной, мы войдём столько же раз, сколько выйдем из неё. Поэтому степени всех вершин должны быть чётными, кроме двух, а значит, эйлеров граф имеет не более двух нечётных вершин.
Вывод: используя закономерности Эйлера, можно безошибочно распознавать, какие фигуры нельзя нарисовать одним росчерком и какие можно, а также, с какой точки надо начинать вычерчивание.
-
Информационные модели на графах
Для того, чтобы представить информацию о составе и структуре системы графически, необходимо в виде чертежа изобразить компоненты системы и соединить их между собой какими-либо линиями.
Граф - это средство для наглядного представления состава и структуры системы.
Вершина графа- это компоненты системы, изображаемые кругами, овалами, прямоугольниками…
Дуги - это направленные линии (стрелки), связывающие компоненты между собой определенным образом.
Ребра- это ненаправленная линия, связывающая компоненты собой определенным образом.
Дерево – это граф, предназначенный для отображения вложенности, подчиненности, наследственности и так далее между объектами. Каждая вершина связана только с верхней и не связана больше ни с чем. В таком графе нет связанных по замкнутой линии вершин.
Сеть- это граф, в котором вершины связаны между собой по принципу «многие ко многим».
Блок-схема - это граф, отображающий последовательность выполнения действий. Его вершины отображают отдельные действия и изображаются определенными геометрическими фигурами, а связи изображаются дугами.
ГЛАВА II. ЗАДАЧИ НА ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ
Возникает вопрос: нужны ли графы при решении задач? Разве нельзя прийти к решению чисто логическим путём? Можно. Используя графы, решение задач становится проще и нагляднее.
Если представить задачи, графы которых имеют 100 или более вершин, то понятно, что без графов не обойтись. Именно такие задачи приходится решать современным инженерам и экономистам. Сейчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике – при построении электрических схем, в химии и биологии – при изучении молекул и их цепочек, в экономике при решении задач о выборе оптимального пути для потоков грузового транспорта и во многих других задачах.
В математике с теорией графов связаны не только математические развлечения и головоломки, но и более серьёзные задачи.
Очень интересна задача о Кенигсбергских мостах (эта задача еще называется Эйлеровской): задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. "Кенигсбергские же мосты расположены так, что их можно представить на следующем рисунке, на котором A обозначает остров, а B, C и D - части континента, отделенные друг от друга рукавами реки. Семь мостов обозначены буквами a, b, c, d, e, f, g ".
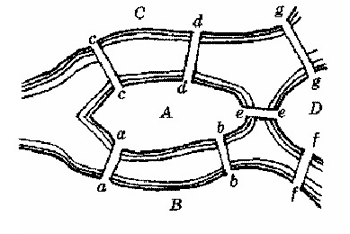 рис.6
рис.6
Ход решения задачи будем представлять в виде графа, где вершины - острова и берега, а ребра - мосты.
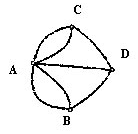 рис7
рис7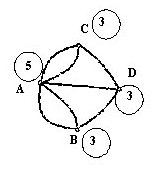 рис.8
рис.8
Нам нужно определить степень каждой вершины и узнать, какие вершины четные, а какие нечетные. Подпишем степени вершин в кружочках. И посчитаем количество нечетных вершин. Нечетные вершины: А, B, C, D.(рис.8) Когда это определено, применяем следующее правило: если все вершины имеют четную степень, то тогда обход, о котором идет речь, возможен, и начать этот обход можно с любого участка. Если же из этих вершин две нечетные, то и тогда можно совершить переход, как это предписано, но только начало обхода непременно должно быть взято в одной из этих двух вершин, а конец обхода непременно должен быть во второй нечетной вершине. Если, наконец, больше двух нечетных вершин, то тогда такое движение вообще невозможно... Итак, используя правило Леонардо Эйлера мы можем сделать вывод: « Так как количество нечетных вершин в графе равно 4, а это 2, то обойти все Кенигсбергские мосты, проходя только один раз через каждый из этих мостов нельзя».
После изучения теоретической части, я решила следующие задачи.
-
Задачи, решаемые «одним росчерком пера»
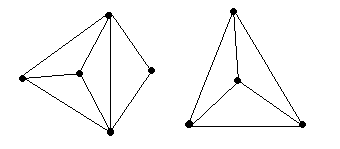 Задача 1. Можно ли нарисовать графы, изображенные на рисунках (9 и 10), не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?[2]
Задача 1. Можно ли нарисовать графы, изображенные на рисунках (9 и 10), не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?[2]
Рис.9 Рис. 10
Решение:
Рис 9. Можно, т. к. только 2 нечетные вершины.
Рис 10. Нельзя, т. к. 4 нечетные вершины.
Задача 2. Можно ли обвести карандашом, не отрывая его от бумаги и не проходя по одной линии дважды, правильный пятиугольник с диагоналями? [3]
Р ешение: Если пятиугольник – граф и все вершины его четные, то это выполнить можно.
ешение: Если пятиугольник – граф и все вершины его четные, то это выполнить можно.
Рис. 11
Задача 3. Дан кусок проволоки длиной 120 см. Можно ли, не ломая проволоки, изготовить каркас куба с ребром 10 см? [4]
Р ешение: рис.12
ешение: рис.12
Если куб – граф, тогда он имеет более двух нечетных вершин (8).
Значит, невозможно изготовить такой каркас, не ломая проволоки.
Задача 4. Не отрывая карандаша от бумаги и не проводя по одной линии дважды, можно ли начертить «открытый конверт» [2]
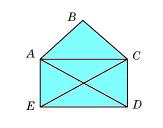 Рис. 13
Рис. 13
Решение: т.к. изображенный конверт – граф, он имеет две нечетные вершины, значит можно.
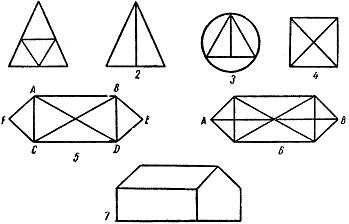
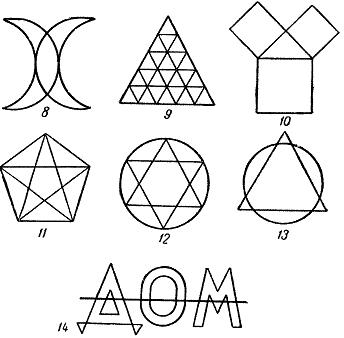
Задача 5. Определите, какие фигуры можно построить одним росчерком карандаша, а какие нельзя.[2,3,4]
Решение: рис 1, 5 – можно, т.к. все вершины четные; рис 2, 3, 6 - можно, т.к всего две нечетные вершины; рис. 4,7 нельзя т.к. нечетных вершин больше, чем четных. (Приложение 1: рисунки с 1 – 7.); рис 8 -14 можно, т.к. все вершины четные. (Приложение 1: рисунки с 8-14.)
Вывод: при решении задач одним росчерком пера при условии, что нужно, не отрывая карандаша от бумаги и не проводя по одной линии дважды, нетрудно разобраться и показать, какую из любых данных фигур можно вычертить одним росчерком, без повторения, а какую нет. Каждую из задач подобного рода можно свести к эйлеровским закономерностям.
2.Задачи, решаемые в школьном курсе математики (задачи 5-9 классов)
Задача №1 Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
Р
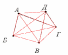 ешение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию - отрезок или часть кривой, соединяющая конкретные точки - имена.
ешение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию - отрезок или часть кривой, соединяющая конкретные точки - имена.
Рис 14 Рис 15
Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
Задача №2 В трех различных домах живут три поссорившиеся между собой соседа. Недалеко от их домов имеются три колодца. Можно ли от каждого дома проложить к каждому из колодцев тропинку так, чтобы никакие две из них не пересекались?
Решение:
Построим граф, вершины которого А, Б, В, 1, 2, 3
соответствуют домам и колодцам условия задачи, и попробуем доказать, что девятую тропинку — ребро графа, не пересекающее остальные ребра, провести нельзя.
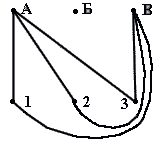
 Рис 16 Рис 17
Рис 16 Рис 17
Проведенные в графе на рисунке ребра А1, А2, A3 и В1, В2, ВЗ (соответствующие тропинкам от домов А и В ко всем колодцам). Построенный граф разбил плоскость на три области: X, У, Z. Вершина Б, в зависимости от ее расположения на плоскости, попадает в одну из этих трех областей. Если рассмотреть каждый из трех случаев «попадания» вершины Б в одну из областей X, Y или Z, то можно увидеть, что всякий раз одна из вершин графа 1, 2 или 3 (один из колодцев) будет «недоступной» для вершины Б (т. е. нельзя будет провести одно из ребер Б1, Б2 или Б3, которое не пересекло бы уже имеющихся в графе ребер).Таким образом, ответ на вопрос задачи будет таким: «Нельзя!» (Именно в таких задачах действует теорема Понтрягина - Куратовского, где, условие задачи в общем можно свести к выяснению вопроса - является ли рассматриваемый граф плоским или нет).
Задача№3.Одежда
У Даши 4 блузки - красная, желтая, голубая и зеленая, и две юбки – синяя и оранжевая. Сколько у нее вариантов подбора костюма?
Решение: (Приложение 2, рис 15). Ответ: 8
Задача №4 Меню
В школьной столовой на первое можно заказать щи, гороховый суп и борщ, на второе котлету и рыбу, а на третье чай и морс. Сколько вариантов обеда можно получить из указанных блюд?
Решение: (Приложение 2, рис 16). Ответ: 12.
-
Задачи, решаемые с использованием информационных моделей на графах
Задача№1
Я поставила перед собой вопрос, можно ли использовать графы при обработке результатов анкетирования? Одним из вопросов анкеты, которую я предложила своим одноклассникам, был следующий: «Какие предметы (указать 2) ты хочешь изучать наиболее глубоко и основательно?». В анкетировании принимали участие 9 человек. При обработке ответов я получила следующие данные: математику выбрали -1 человек, русский - 4, английский язык -1, информатику - 2, биологию - 2, историю - 2, физику - 1, обществознание -1. Ответы на этот вопрос я представила в виде следующего графа. (Приложение 3, рис 17)
Задача №2. На графе изображена система возможного переливания крови. (Приложение 3, рис 18)
Задача №3. Нарисуйте в виде графа систему, состоящую из одноклассников, между которыми существует следующие взаимоотношения: дружат Андрей и Даша, Андрей и Маша, Даша и Коля, Коля и Андрей. (Приложение 3, рис 19)
Задача №4. Укажите результат выполнения действий (Приложение 3, 20) Ответ: а) отрицательное, б) 17.
Задача №5. Построить граф классификации геометрических объектов. (Приложение 4, рис 21).
Решение: Среди геометрических объектов можно выделить линии, плоские фигуры и объемные тела. Среди линий, в свою очередь, выделяются прямые, кривые и ломаные. Среди плоских фигур – круги, эллипсы, параллелограммы и трапеции и т. д.
Стоит отметить, что классификация в данном случае неполная. Например, отсутствует первичный геометрический объект, с которого все начинается, - точка. Обратим внимание на то, что приведенная классификация не является деревом. Объект «квадрат» имеет сразу двух предков – прямоугольник и ромб. Это означает, что любой квадрат обладает всеми свойствами прямоугольника и в то же время всеми свойствами ромба.
Задача №6. Какое значение получится на выходе схемы на рисунке, если на вход подать: а) число 3; б) число 1;в) число 25? (Приложение 3, рис 22). Ответ: а) 7; б) 5; в) 4,5.
Логическая задача.
На соревнованиях по лёгкой атлетике Андрей, Боря, Серёжа и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись:
Даша: Андрей был первым, а Володя вторым. Галя: Андрей был вторым, а Борис – третьим. Лена: Боря был четвёртым, а Серёжа – вторым.
Ася, которая была судьёй на этих соревнованиях, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление. Кто из мальчиков какое место занял?
Решение: Построим граф (Приложение 4, рис.23). Слова девочек построим линиями разного типа. Так как каждая девочка сделала только одно правильное заявление, то надо оставить только по одной линии каждого типа. Предположим, что у Даши второе утверждение верное. Тогда надо убрать А-1, А-2 и С-2. Осталось по одной линии каждого вида, но этот вариант невозможен, т.к. Боря не может занять два места. (Приложение 4, рис.24). Значит второе заявление Даши неверное, а верно первое (убираем В-2). Убираем А-2 и оставляем Б-3. Убираем Б-4 и оставляем С-2. В итоге имеем: Андрей - 1 место, Борис - 3, Серёжа - 2, Володя – 4. (Приложение 4, рис.25)
ЗАКЛЮЧЕНИЕ
В работе рассмотрены графы, области их применения, решено несколько задач с помощью графов. Приёмы решения задач с использованием графов подкупают своей естественностью и простотой, избавляют от лишних рассуждений, во многих случаях сокращающих нагрузку на память. С одной стороны, графы помогают проследить все логические возможности изучаемой ситуации, с другой, благодаря своей обозримости, помогают тут же, в ходе решения задач, классифицировать логические возможности, отбрасывать неподходящие случаи, не доводя до полного перебора всех случаев. Графовые задачи обладают рядом достоинств, позволяющих их использовать для развития воображения и улучшения логического мышления, применимы в решении многих задач.
Итак, в результате своей исследовательской работы я познакомилась с понятием «графа», узнала об истории возникновения науки «теория графов», а главное научилась строить графы и решать с их помощью разные задачи.
Гипотеза подтвердилась, действительно решение задач по различным предметам упрощается, если удается использовать теорию графов.
Для своей работы я решила необычные задачи, которые меня заинтересовали. В дальнейшем надеюсь лучше изучить графы и постараться решить другие, более сложные задачи.
СПИСОК ЛИТЕРАТУРЫ
1.Математика: Учеб. Для 5-6 кл. общеобразоват. учреждений / Г.В. Дорофеев, И.Ф. Шарыгин и др., Под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – М.: Просвещение,2001 -368с.
2. Нестеренко Ю.В. Задачи на смекалку.- М.: Дрофа, 2005.-233с.
3. Перельман Я.И. Веселые задачи. - М.: АсрельАст,2005. – 287с.
4. Сборник олимпиадных задач по математике, В. Г. Горбачев, 2004г.
5. Энциклопедия для детей. Математика. Том 11. М.: Акванта+, 2001.
6. Я познаю мир. Математика.- М.: Аст, 1998
7. Н.С. Новиков. Дискретная математика. СПб.: Питер, 2001.
8. А.Г.Мордкович, П.В. Семёнов. События, вероятности, статистическая обработка данных. 7-9 класс.
9. Коннова Л.П. Знакомьтесь, графы. – Самара,2001.
10. В.А Гусев, А.И Орлов, А.Л Розенталь. Внеклассная работа по математике в 6-8 классах. Москва « Просвещение» , 1997
11. http://www.khspu.ru
ПРИЛОЖЕНИЕ 1
1
ПРИЛОЖЕНИЕ 2
 Рис.15
Рис.15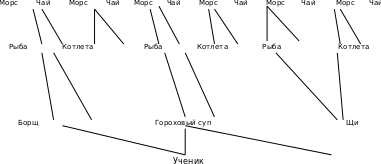 Рис.16 ПРИЛОЖЕНИЕ 3
Рис.16 ПРИЛОЖЕНИЕ 3
Н


 .И. ХИМИЯ
.И. ХИМИЯ
Г
 .А. АНГЛИЙСКИЙ
.А. АНГЛИЙСКИЙ
\


 М.П. РУССКИЙ
М.П. РУССКИЙ
К
 .Д. МАТЕМАТИКА
.Д. МАТЕМАТИКА
В .К. ИНФОРМАТИКА
.К. ИНФОРМАТИКА
Ш .П. БИОЛОГИЯ
.П. БИОЛОГИЯ
Ф .А. ИСТОРИЯ
.А. ИСТОРИЯ
М .К. ФИЗИКА
.К. ФИЗИКА
Л.Ю. ОБЩЕСТВОЗНАНИЕ Рис. 17
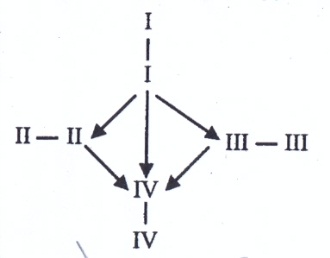

Рис 18
Рис 19
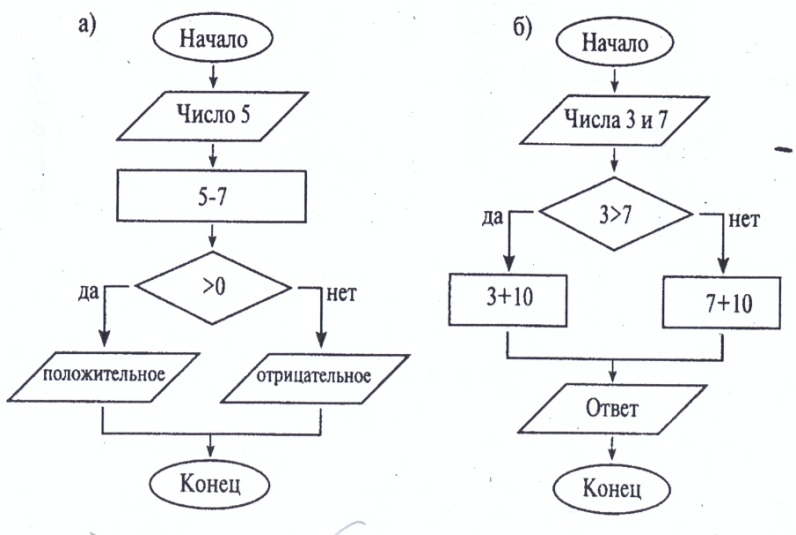 Рис 20
Рис 20
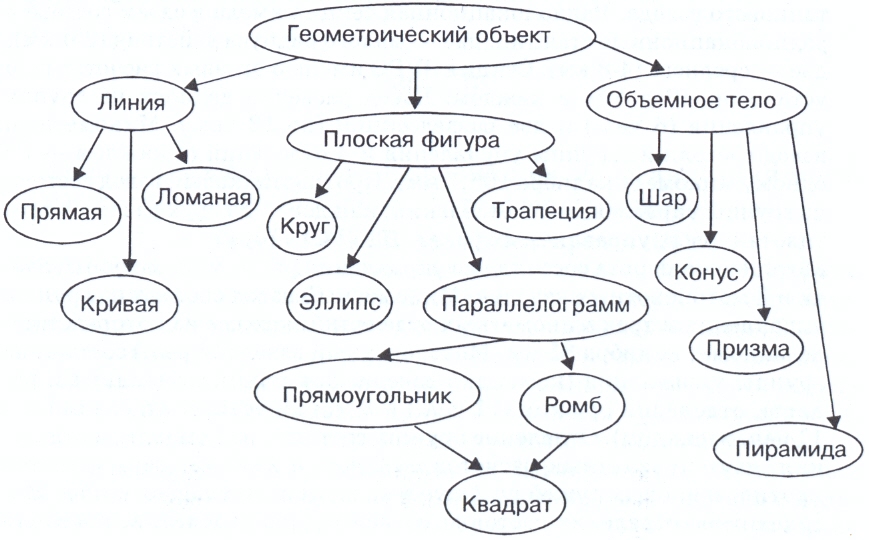 Рис 21
Рис 21
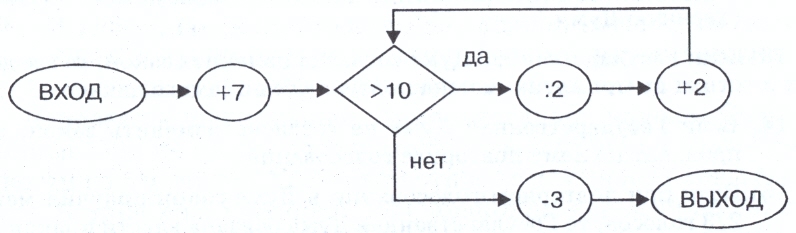 Рис 22
Рис 22
ПРИЛОЖЕНИЕ 4








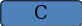



РИС.23









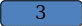

РИС.24









РИС.25
16







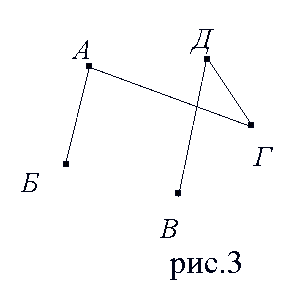


 исло игр, проведённых к данному моменту, равно числу рёбер, то есть 7.
исло игр, проведённых к данному моменту, равно числу рёбер, то есть 7.
 рис.6
рис.6 рис7
рис7 рис.8
рис.8 Задача 1. Можно ли нарисовать графы, изображенные на рисунках (9 и 10), не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?[2]
Задача 1. Можно ли нарисовать графы, изображенные на рисунках (9 и 10), не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз?[2] ешение: Если пятиугольник – граф и все вершины его четные, то это выполнить можно.
ешение: Если пятиугольник – граф и все вершины его четные, то это выполнить можно.  ешение: рис.12
ешение: рис.12 Рис. 13
Рис. 13
 ешение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию - отрезок или часть кривой, соединяющая конкретные точки - имена.
ешение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию - отрезок или часть кривой, соединяющая конкретные точки - имена.
 Рис 16 Рис 17
Рис 16 Рис 17

 Рис.15
Рис.15 Рис.16 ПРИЛОЖЕНИЕ 3
Рис.16 ПРИЛОЖЕНИЕ 3


 .И. ХИМИЯ
.И. ХИМИЯ
 .А. АНГЛИЙСКИЙ
.А. АНГЛИЙСКИЙ


 М.П. РУССКИЙ
М.П. РУССКИЙ
 .Д. МАТЕМАТИКА
.Д. МАТЕМАТИКА .К. ИНФОРМАТИКА
.К. ИНФОРМАТИКА .П. БИОЛОГИЯ
.П. БИОЛОГИЯ .А. ИСТОРИЯ
.А. ИСТОРИЯ .К. ФИЗИКА
.К. ФИЗИКА

 Рис 20
Рис 20 Рис 21
Рис 21 Рис 22
Рис 22