Тема: Анализ таблиц истинности логических выражений.
Что нужно знать:
¬ A, 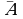 не A (отрицание, инверсия)
не A (отрицание, инверсия)
A B,  A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция)
A B,  A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)
A → B импликация (следование)
A B эквивалентность (равносильность)
A → B = ¬ A B или в других обозначениях A → B = 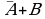
¬ (A B) = ¬ A ¬ B 
¬ (A B) = ¬ A ¬ B 
если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»
таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных
если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);
количество разных логических функций, удовлетворяющих неполной таблице истинности, равно 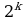 , где
, где  – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)
логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)
логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно
эквивалентность АB равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1
Пример 1.
Логическая функция F задаётся выражением (¬z) x x y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z?
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение (через полную таблицу):
запишем заданное выражение в более простых обозначениях:

общий ход действий можно описать так: подставляем в эту формулу какое-нибудь значение (0 или 1) одной из переменных, и пытаемся определить, в каком столбце записана эта переменная;
например, подставим x = 0, при этом сразу получаем F = 0; видим, что переменная x не может быть ни в первом, ни во втором столбце (противоречие во 2-й строке):
| ? | ? | ? | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
а в третьем – может:
| ? | ? | x | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
подставим x = 1, тогда  ; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что
; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что  только в одном случае – при z = 1 и y = 0;
только в одном случае – при z = 1 и y = 0;
ищем такую строчку, где x = 1 и  :
:
| ? | ? | x | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
как мы видели, в этой строке таблицы должно быть обязательно z = 1 и y = 0; поэтому z – в первом столбце, а y – во втором
Ответ: zyx.
Решение (преобразование логического выражения):
Используя законы алгебры логики, а именно распределительный для операции «ИЛИ» (см. учебник 10 кл. 1 часть, стр. 185), запишем заданное выражение:
 ;
;
Поскольку добиться логической единицы в произведении сложнее, чем в сумме рассмотрим строки таблицы, где произведение равно 1(это 2-я, 4-я и 8-я строки );
Во 2-й строке Х обязательно должно быть равно 1. Поэтому Х может быть только в третьем столбце, в первых двух могут быть и Y, и Z.
Анализируя 4 строку приходим к выводу, что в первом столбце таблицы может быть только Z, во втором – Y.
В 8-й строке убеждаемся в верности своих рассуждений:
Т.о., немного упростив выражение, уменьшили количество рассматриваемых строк.
Ответ: zyx.
Решение (преобразование логического выражения):
Рассмотрим строки таблицы, где функция равна 1
| a | b | c | F |
|
| 0 | 0 | 1 | 1 | 
|
| 0 | 1 | 1 | 1 | 
|
| 1 | 1 | 1 | 1 | 
|
и построим логическое выражение для заданной функции, обозначив переменные через a, b и с (см. § 22 из учебника для 10 класса):
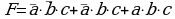
Упрощаем это выражение, используя законы алгебры логики:
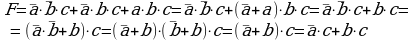
Сравнивая полученное выражение с заданным  , находим, что a = z, b = y и c = x.
, находим, что a = z, b = y и c = x.
Ответ: zyx.
Решение (сопоставление таблиц истинности):
Рассмотрим строки таблицы, где функция равна 1, обозначив переменные через a, b и с
| a | b | c | F |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
и сопоставим эти строки с теми строками таблицы истинности заданной функции  , где F = 1:
, где F = 1:
| x | y | z | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Сравнивая столбцы интересующих нас строк, определяем, что c = x (все три единицы в зеленых ячейках), b = y (один ноль и две единицы) и a = z (два ноля и единица).
Ответ: zyx.
Решение:
Функция  задана в виде ДНФ (дизъюнктивной нормальной формы), которую не сложно привести к СДНФ, используя известные тождества алгебры логики:
задана в виде ДНФ (дизъюнктивной нормальной формы), которую не сложно привести к СДНФ, используя известные тождества алгебры логики:
a ∙ 1 = a и  .
.
Каждую конъюнкцию дополним недостающей переменной:

СДНФ:
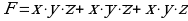
Каждая конъюнкция в СДНФ соответствует строке таблицы истинности, в которой F=1. Используя полученную СДНФ, делаем вывод: в таблице истинности имеется 3 строки, где F=1, заполним их:
|
| x | y | z | F |
| 
| 1 | 1 | 0 | 1 |
| 
| 1 | 0 | 0 | 1 |
| 
| 1 | 1 | 1 | 1 |
В таблице, приведенной в задании, рассмотрим строки, где F=1:
| ? | ? | ? | F |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Сравнивая столбцы этих таблиц, делаем выводы:
в первом (жёлтом) столбце таблицы задания находится z (одна единица),
во втором (синем) столбце таблицы задания находится y (две единицы),
в последнем (зелёном) столбце таблицы задания находится x (все единицы).
Ответ: zyx.
Пример 2.
Каждое логическое выражение A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы. Каково минимально возможное число единиц в столбце значений таблицы истинности выражения A B?
Решение:
полная таблица истинности каждого выражения с пятью переменными содержит 25 = 32 строки
в каждой таблице по 4 единицы и по 28 (= 32 – 4) нуля
выражение A B равно нулю тогда и только тогда, когда A = 0 и B = 1
минимальное количество единиц в таблице истинности выражения A B будет тогда, когда там будет наибольшее число нулей, то есть в наибольшем количество строк одновременно A = 0 и B = 1
по условию A = 0 в 28 строках, и B = 1 в 4 строках, поэтому выражение A B может быть равно нулю не более чем в 4 строках, оставшиеся 32 – 4 = 28 могут быть равны 1
Ответ: 28.
Пример 3.
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
|
| 0 |
|
|
|
|
| 1 | 1 |
| 1 |
|
| 0 |
|
|
|
| 0 |
|
|
|
| 1 |
|
|
| 1 | 0 |
Каким выражением может быть F?
1) ¬x1 x2 x2 ¬x3 ¬x4 x2 ¬x5 x5 x6 ¬x7 ¬x8
2) (x1 ¬x2 ¬x3 x4) (x5 x6 ¬x7 x8)
3) x1 ¬x8 ¬x3 x4 x5 ¬x6 ¬x7 x8
4) x1 ¬x4 x2 x3 ¬x4 ¬x5 ¬x6 ¬x7 ¬x8
Решение:
перепишем выражения в более простой форме, заменив «И» () на умножение и «ИЛИ» () на сложение:
1) 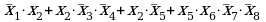
2) 
3) 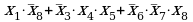
4) 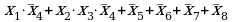
cреди заданных вариантов ответа нет «чистых» конъюнкций и дизъюнкций, поэтому мы должны проверить возможные значения всех выражений для каждой строки таблицы
подставим в эти выражения известные значения переменных из первой строчке таблицы,  и
и  :
:
1) 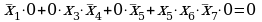
2) 
3) 
4) 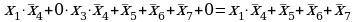
видим, что первое выражение при  и
и  всегда равно нулю, поэтому вариант 1 не подходит; остальные выражения вычислимы, то есть, могут быть равны как 0, так и 1
всегда равно нулю, поэтому вариант 1 не подходит; остальные выражения вычислимы, то есть, могут быть равны как 0, так и 1
подставляем в оставшиеся три выражения известные данные из второй строчки таблицы,  и
и  :
:
2) 
3) 
4) 
видим, что выражение 4 при этих данных всегда равно 1, поэтому получить F=0, как задано в таблице, невозможно; этот вариант не подходит
остаются выражения 2 и 3; подставляем в них известные данные из третьей строчки таблицы,  и
и  :
:
2) 
3) 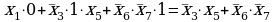
Выражение 2 в этом случае всегда равно 1, поэтому оно не подходит (по таблице истинности оно должно быть равно 0); выражение 3 вычислимо, это и есть правильный ответ
Ответ: 3.
Пример 4.
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Какое выражение соответствует F?
1) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8
2) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8
3) ¬(x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8
4) (x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8
Решение:
перепишем выражение в более простой форме, заменив «И» () на умножение и «ИЛИ» () на сложение:

в этом задании среди значений функции только одна единица, как у операции «И», это намекает на то, что нужно искать правильный ответ среди вариантов, содержащих «И», «НЕ» и импликацию (это варианты 1 и 3)
действительно, вариант 2 исключён, потому что при x4=1 во второй строке получаем 1, а не 0
аналогично, вариант 4 исключён, потому что при x5=1 в первой строке получаем 1, а не 0
итак, остаются варианты 1 и 3; вариант 1 не подходит, потому что при x6=0 в третьей строке получаем 0, а не 1
проверяем подробно вариант 3, он подходит во всех строчках
Ответ: 3.
Пример 5.
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | F |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
Одно из приведенных ниже выражений истинно при любых значениях переменных x1, x2,x3, x4, x5. Укажите это выражение.
1) F(x1,x2,x3,x4,x5)x1
2) F(x1,x2,x3,x4,x5)x2
3) F(x1,x2,x3,x4,x5)x3
4) F(x1,x2,x3,x4,x5)x4
Решение:
во всех заданных вариантах ответа записана импликация, она ложна только тогда, когда левая часть (значение функции F) истинна, а правая – ложна.
выражение 1 ложно для набора переменных в третьей строке таблицы истинности, где F(…) = 1 и  , оно не подходит
, оно не подходит
выражение 2 ложно для набора переменных в третьей строке таблицы истинности, где F(…) = 1 и  , оно не подходит
, оно не подходит
выражение 3 истинно для всех наборов переменных, заданных в таблице истинности
выражение 4 ложно для набора переменных в первой строке таблицы истинности, где F(…) = 1 и  , оно не подходит
, оно не подходит
ответ: 3.
Пример 6.
Дано логическое выражение, зависящее от 5 логических переменных:
z1 ¬z2 ¬z3 ¬z4 z5
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение:
перепишем выражение, используя другие обозначения:

это выражение с пятью переменными, которые могут принимать 25 = 32 различных комбинаций значений
сначала определим число K комбинаций переменных, для которых выражение истинно; тогда число комбинаций, при которых оно ложно, вычислится как 32 – K
заданное выражение истинно только тогда, когда истинно любое из двух слагаемых:  ,
, 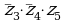 или оба они истинны одновременно
или оба они истинны одновременно
выражение  истинно только при
истинно только при 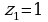 и
и  , при этом остальные 3 переменных могут быть любыми, то есть, получаем всего 8 = 23 вариантов
, при этом остальные 3 переменных могут быть любыми, то есть, получаем всего 8 = 23 вариантов
выражение 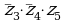 истинно только при
истинно только при  и
и 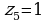 , при этом остальные 2 переменных могут быть любыми, то есть, получаем всего 4 = 22 варианта
, при этом остальные 2 переменных могут быть любыми, то есть, получаем всего 4 = 22 варианта
заметим, что один случай, а именно  ,
,  обеспечивает истинность обоих слагаемых в исходном выражении, то есть, входит в обе группы (пп. 3 и 4), поэтому исходное выражение истинно для 11 = 8 + 4 – 1 наборов значений переменных, а ложно – для 32 – 11 = 21 набора.
обеспечивает истинность обоих слагаемых в исходном выражении, то есть, входит в обе группы (пп. 3 и 4), поэтому исходное выражение истинно для 11 = 8 + 4 – 1 наборов значений переменных, а ложно – для 32 – 11 = 21 набора.
ответ: 21.
Пример 7.
Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
1) (x1 x2) ¬x3 x4 ¬x5 x6 ¬x7
2) (x1 x2) ¬x3 x4 ¬x5 x6 x7
3) (x1 ¬x2) x3 ¬x4 ¬x5 x6 ¬x7
4) (¬x1 ¬x2) x3 ¬x4 x5 ¬x6 x7
Решение:
в последнем столбце таблицы всего одна единица, поэтому стоит попробовать использовать функцию, состоящую из цепочки операций «И» (ответы 1, 3 или 4);
для этой «единичной» строчки получаем, что инверсия (операция «НЕ») должна быть применена к переменным x3, x5 и x7, которые равны нулю:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
таким образом, остается только вариант ответа 1 (в ответах 3 и 4 переменная x3 указана без инверсии)
проверяем скобку (x1 x2): в данном случае она равна 1, что соответствует условию
ответ: 1.

| X | Y | Z | F |
| 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Пример 8.
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?
1) ¬X ¬Y ¬Z 2) X Y Z 3) X Y Z 4) ¬X ¬Y ¬Z
Решение:
нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных
если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F, оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F
перепишем ответы в других обозначениях:
1)  2)
2) 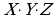 3)
3) 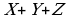 4)
4) 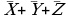
первое выражение,  , равно 1 только при
, равно 1 только при  , поэтому это неверный ответ (первая строка таблицы не подходит)
, поэтому это неверный ответ (первая строка таблицы не подходит)
второе выражение, 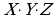 , равно 1 только при
, равно 1 только при  , поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
, поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
третье выражение,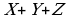 , равно нулю при
, равно нулю при  , поэтому это неверный ответ (вторая строка таблицы не подходит)
, поэтому это неверный ответ (вторая строка таблицы не подходит)
наконец, четвертое выражение, 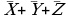 равно нулю только тогда, когда
равно нулю только тогда, когда  , а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности
, а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности
таким образом, правильный ответ – 4 ; частичная таблица истинности для всех выражений имеет следующий вид:
| X | Y | Z | F | 
| 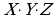
| 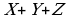
| 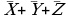
|
| 1 | 0 | 0 | 1 | 0 × | 0 × | 1 | 1 |
| 0 | 0 | 0 | 1 | – | – | 0 × | 1 |
| 1 | 1 | 1 | 0 | – | – | – | 0 |
(красный крестик показывает, что значение функции не совпадает с F, а знак «–» означает, что вычислять оставшиеся значения не обязательно).

| X | Y | Z | F |
| 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Пример 9.
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) ¬X ¬Y ¬Z 2) X Y Z 3) X ¬Y ¬Z 4) X ¬Y ¬Z
Решение:
перепишем ответы в других обозначениях:
1)  2)
2) 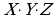 3)
3)  4)
4) 
в столбце F есть единственная единица для комбинации 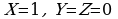 , простейшая функция, истинная (только) для этого случая, имеет вид
, простейшая функция, истинная (только) для этого случая, имеет вид  , она есть среди приведенных ответов (ответ 3)
, она есть среди приведенных ответов (ответ 3)
таким образом, правильный ответ – 3.
Пример 10.
Дано логическое выражение, зависящее от 5 логических переменных:
X1 ¬X2 X3 ¬X4 X5
Сколько существует различных наборов значений переменных, при которых выражение ложно?
1) 1 2) 2 3) 31 4) 32
Решение:
перепишем выражение в других обозначениях:

таблица истинности для выражения с пятью переменными содержит 25 = 32 строки (различные комбинации значений этих переменных)
логическое произведение истинно в том и только в том случае, когда все сомножители равны 1, поэтому только один из этих вариантов даст истинное значение выражения, а остальные 32 – 1 = 31 вариант дают ложное значение.
таким образом, правильный ответ – 3.
Пример
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
Какое выражение соответствует F?
1) ¬x1 x2 ¬x3 x4 x5 ¬x6 ¬x7
2) ¬x1 x2 ¬x3 x4 ¬x5 ¬x6 x7
3) x1 ¬x2 x3 ¬x4 x5 x6 ¬x7
4) x1 ¬x2 x3 ¬x4 ¬x5 x6 ¬x7
Решение (вариант 2):
перепишем выражения 1-4 в других обозначениях:

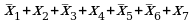

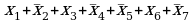
поскольку в столбце F есть два нуля, это не может быть выражение, включающее только операции «ИЛИ» (логическое сложение), потому что в этом случае в таблице был бы только один ноль, поэтому варианты 2 и 4 отпадают:


аналогично, если бы в таблице был один ноль и две единицы, это не могла бы быть цепочка операций «И», которая всегда дает только одну единицу;
для того, чтобы в последней строке таблицы получилась единица, нужно применить операцию «НЕ» (инверсию) к переменным, значения которых в этой строке равны нулю, то есть к 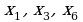 и
и  ; остальные переменные инвертировать не нужно, так как они равны 1; видим, что эти условия в точности совпадают с выражением 1, это и есть правильный ответ
; остальные переменные инвертировать не нужно, так как они равны 1; видим, что эти условия в точности совпадают с выражением 1, это и есть правильный ответ
Ответ: 1.







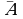 не A (отрицание, инверсия)
не A (отрицание, инверсия) A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция) A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)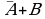


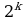 , где
, где  – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
 ; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что
; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что  только в одном случае – при z = 1 и y = 0;
только в одном случае – при z = 1 и y = 0; ;
;
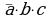

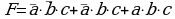
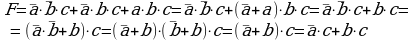
 задана в виде ДНФ (дизъюнктивной нормальной формы), которую не сложно привести к СДНФ, используя известные тождества алгебры логики:
задана в виде ДНФ (дизъюнктивной нормальной формы), которую не сложно привести к СДНФ, используя известные тождества алгебры логики:  .
. 
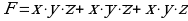



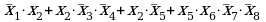

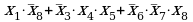
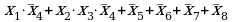
 и
и  :
: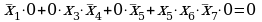


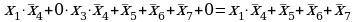
 и
и  :
:


 и
и 
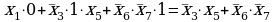

 , оно не подходит
, оно не подходит 
 ,
, 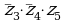 или оба они истинны одновременно
или оба они истинны одновременно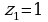 и
и  , при этом остальные 3 переменных могут быть любыми, то есть, получаем всего 8 = 23 вариантов
, при этом остальные 3 переменных могут быть любыми, то есть, получаем всего 8 = 23 вариантов и
и 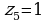 , при этом остальные 2 переменных могут быть любыми, то есть, получаем всего 4 = 22 варианта
, при этом остальные 2 переменных могут быть любыми, то есть, получаем всего 4 = 22 варианта  ,
,  обеспечивает истинность обоих слагаемых в исходном выражении, то есть, входит в обе группы (пп. 3 и 4), поэтому исходное выражение истинно для 11 = 8 + 4 – 1 наборов значений переменных, а ложно – для 32 – 11 = 21 набора.
обеспечивает истинность обоих слагаемых в исходном выражении, то есть, входит в обе группы (пп. 3 и 4), поэтому исходное выражение истинно для 11 = 8 + 4 – 1 наборов значений переменных, а ложно – для 32 – 11 = 21 набора.
 2)
2) 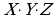 3)
3) 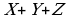 4)
4) 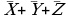
 , поэтому это неверный ответ (первая строка таблицы не подходит)
, поэтому это неверный ответ (первая строка таблицы не подходит) , поэтому это неверный ответ (первая и вторая строки таблицы не подходят)
, поэтому это неверный ответ (первая и вторая строки таблицы не подходят) 4)
4) 
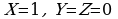 , простейшая функция, истинная (только) для этого случая, имеет вид
, простейшая функция, истинная (только) для этого случая, имеет вид 

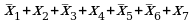

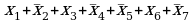
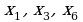 и
и  ; остальные переменные инвертировать не нужно, так как они равны 1; видим, что эти условия в точности совпадают с выражением 1, это и есть правильный ответ
; остальные переменные инвертировать не нужно, так как они равны 1; видим, что эти условия в точности совпадают с выражением 1, это и есть правильный ответ









